ДМ
.pdf

8.Матричное представление бинарных отношений. Свойства матрицы бинарных отношений.

9.Отношение эквивалентности. Примеры. Разбиение множества.
Бинарное отношение заданное на не пустом множестве А, называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Классы эквивалентности порождённые элементом а называется множество элементов из множества А находящиеся с
элементом а в отношении Р.
Множество всех классов эквивалентности по отношению к Р называется фактор множества 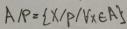
Любой элемент класса эквивалентности называется её представителем.

Разбиение не пустого множества А называется совокупностью его не пустых подмножеств, таких что объединение всех подмножеств – есть множество А. А пересечение любых двух подмножеств есть не пустое множество.
10.Отношение порядка. Диаграммы Хассе. Примеры.


11. Отображения и их виды. Свойства функций. Примеры.

˂ -- ˃ - этот знак показывает, что например А ˂ -- ˃ В (биекция между множествами)

12. Конечные и бесконечные множества. Равномощность. Примеры. Счетные и несчетные множества. Примеры.


