ДМ

1. Метод математической индукции ПЕРВАЯ ЧАСТЬ

Математическая индукция — метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером — база (базис) индукции, а затем доказывается, что если верно утверждение с номером , то верно и следующее утверждение с номером — шаг индукции, или индукционный переход.

2. Комбинаторика. Основные определения. Правило суммы и произведения. Примеры. Метод включений и исключений.

Комбинаторика – это раздел дискретной математики, посвящённый решению задач пересчёта и перечисления элементов некоторого множества.

Определения:

1)Подмножество их r-элементов выбранное из множества Sn состоящее из n элементов называется (n,r) – выборка, r – называется объёмом этой выборки.

2)Выборка называется упорядоченной, если порядок следования элементов задан.

3)Две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются различными.

4)Если порядок следования элементов не является существенным, то выборка называется неупорядоченной.

5)В выборке могут быть повторения элементов, а могут и не допускаться повторения.

6)Упорядоченная (n,n)–выборка, в которой элементы могут повторяться называется упорядоченной с повторениями. P – перестановка. Число (n,n)–перестановок с повторениями обозначается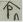

,которые тожественны между собой и отличны от элементов входящих в другие группы. Тождество — равенство двух выражений, выполняющееся на всём множестве допустимых значений, входящих в эти выражения переменных.

7)Упорядоченная (n,n)–выборка, в которой элементы попарно различны, называется (n,n)-перестановка без повтора. Pn=n!

8)Упорядоченная (n,r)–выборка, в которой элементы могут повторяться называется размещением с повторением

(n,r). Число (n,r) – размещения с повторением

Упорядоченная (n,r)–выборка, элементы которой попарно различны называются (n,r) размещением без повторений.

Число (n,r) – размещение без повторений.

Неупорядоченная (n,r)–выборка, в которой элементы попарно различны называется сочетанием без повторений.

Неупорядоченная (n,r)–выборка, элементы которой могут повторяться называется сочетанием с повторением.

Число сочетаний с повторениями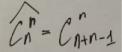

Правило суммы и правило произведения.

Основной комбинаторной задачей является подсчёт числа (n,r)– выборок при различных условиях

Определения:

Правило суммы – Если объект А может быть выбран m способами, а объект В другими n способами при условии, что одновременный выбор А и В невозможен, то выбор А или В можно осуществить m + n способами.

Правило произведения – Если объект А может быть выбран m способами и после каждого из таких выборов объект В с свою очередь может быть выбран n способами, то выбор А и В в указанном порядке может быть осуществлён m*n способами.

Метод включений и исключений

Рассмотрим задачу о нахождении числа элементов объединения множеств. Пусть n(A) – количество элементов в множестве, тогда n(A В) = n(A)+ n(В)- n(A∩В). n(A В С) = n(A)+ n(В)+ n(С)- n(A∩В)- n(A∩С) – n(В∩С) + +n(A∩В∩С).

В объединение () входят все элементы, которые встречались в множествах по отдельности, но только по одному разу. Если A = {100, 200, 300, 400, 500}, B = {100, 500, 1000, 1500}, то A B = {100, 200, 300, 400, 500, 1000, 1500}.

Если H — множество упражнений, укрепляющих руки, и L — множество упражнений, укрепляющих ноги, то H ∩ L

— множество упражнений, укрепляющих руки и ноги. ∩ - пересечение.

3. Бином Ньютона. Основные свойства биномиальных коэффициентов. Треугольник Паскаля. Полиномиальная теорема.

Всякий второй член называется биномом, то есть эта сумма или разность двух алгебраических выражений называемых членами бинома.

Известна формула сокращённого умножения, которая позволяет возвести бином во вторую или третью или четвёртую степень:

Эта формула называется биномом Ньютона.

- называется биноминальным коэффициентом.

7)Треугольник Паскаля – По формуле сложения можно последовательно вычислить (n,k). Вычисляемые таким образом коэффициенты располагают таким образом таблицу, которую называют треугольником Паскаля.

4. Множества, способы задания множества.

Множество – набор или совокупность элементов, объединённых общим свойством. Элементы множества должны быть различными. Множество обозначается заглавными буквами – А,В,С. Пример как записывается множество А = {1;2;3;4;5}, в скобках перечисляются элементы или описываются их свойства.

а А (а принадлежит А). a A (а не принадлежит А).

Множество, в котором нет ни одного объекта называется пустым .

Определения:

Если каждый элемент множества А есть элемент множества В, А В. -подмножество.

Множество состоящее из одних и тех же элементов называется равным А=В. В противном случаем называются

множества неравные А≠В.

Если множество М А, М≠0 и М≠А, то М называется собственным подмножеством множества А.

У любого множества есть обязательно хотя бы два подмножества: пустое множество и само множество. Эти два

подмножества называются несобственными подмножествами.

Совокупность всех подмножеств множества А называют его булеаном Р(А).

Способы задания множества:

1)Перечисление А = {1,2,3,4}

2)С помощью характеризующего свойства – характеристическое свойство – которым обладает каждый элемент входящий в множество и не обладает ни один объект ему не принадлежащий. А={x/P(x)}, множество состоит из элементов х обладающих свойством Р. Запись Х= {x / P(x)} означает, что элемент х принадлежит множеству Х, тогда и только тогда, когда P(x) истинное утверждение. В={p/p-простое число} C={x/x^2+6x+5=0}

3)Указание поражающей процедуры – это процесс, который будучи запущен поражает все элементы данного множества. K={k/k=5n^2+3n+1,где n натуральное число} В примере вначале указывается элемент множества, далее характеристика порождения элемента. Для бесконечных множеств предпочтительнее второй способ описания. Примеры записи: С={x/x^2+5=0,где x действительное число}.

5. Операции над множествами и их свойства.

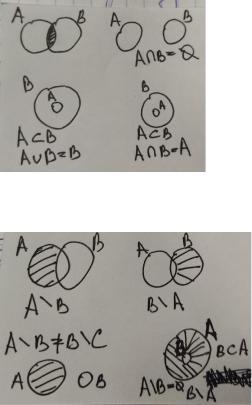
1) Объединение – называется множество, которое обозначается А В состоящее из тех и только тех элементов, которые хотя бы принадлежат одному из множеств А или В.

А В={x/x A или x B}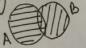

2)Пересечение - называется множество, которое обозначается А ∩ В, которое состоит из тех и только тех элементов принадлежащих одновременно и А и В. А ∩ В = {x/x A u x B}

3.Разность – называется множество А\В, состоящее из тех и только тех элементов, которые входят в А и одновременно не входит в В. А\В={x/x A u x B}

4.Симметрическая разность – называется множество 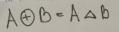состоящее из элементов объединения, но не входящее в пересечение этих множеств.

5.Декартовое произведение (прямое произведение) – называется множество А х В, состоящее из всех упорядоченных пар (a;b) : a A, b B . A x B = {(a;b)/ a A; b B}

Если элемент a A, b B, то пару элементов a и b называют упорядоченной парой, причём пары (a1;b1) и (a2;b2) считаются равными a1 = a2 и b1 = b2.

Декартовое произведение А на себя называется декартовым квадратом А х А = А^2.

6. Бинарные отношения. Способы задания бинарных отношений.

7.Операции над отношениями. Свойства бинарных отношений на множестве.

Для бинарного отношения обычным образом определяется теоретика – множественные операции (объединения и

пересечения) Р – бинарное отношение.

Определение:

Обратным к Р-отношениям(инверсия) называется множество Р^-1 = {(x,y)/(y,x) P} определена угарная операция перехода к обратному отношению.

Композиция бинарного отношения