
5 курс / ОЗИЗО Общественное здоровье и здравоохранение / Осенний семестр / Занятие 2 / 3+
.docxРешение эталонной задачи
На основании нижеприведенных данных требуется:
1.Сгруппировать вариационный ряд.
2.Определить моду (Мо) и медиану (Ме).
3.Рассчитать среднюю арифметическую (простую, взвешенную).
4.Рассчитать среднее квадратическое отклонение (σ).
5.Рассчитать коэффициент вариации (Сv).
6.Рассчитать среднюю ошибку средней арифметической величины (mM).
Ниже представлен вариационный ряд, в котором приведена длительность лечения больных ОРВИ в поликлинике в днях: 11,10,16,13,12,17,6,8,9,10,14,11,10,8,4,5,11,9,12,11,13,4,3,7,5,9,15,11,10, 12,7,11,8,7,10,6,9,15,6,11,12,13,16,18.
Порядок решения:
1. Проводим группировку вариационного ряда, для чего составляем комбинационную таблицу. Это необходимо в связи с тем, что число вариант в вариационном ряду может быть большим и составлять величину 50 – 100 и более. Это затрудняет последующие вычисления.
Для этого определяем число групп в вариационном ряду с тем, чтобы характерные особенности распределения изучаемого признака не были нивелированы.
Рекомендуемое число групп с учетом с учетом числа наблюдений
n (число наблюдений) |
31-45 |
46-100 |
101-200 |
201-500 |
r (число групп) |
6-7 |
8-10 |
11-12 |
12-17 |
В нашем примере число наблюдений составляет – 44, поэтому вариационный ряд должен иметь 6-7 групп.
Теперь определим величину интервала по формуле:
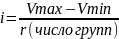 =
=
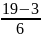 = 2,7
= 2,7
Полученный интервал рекомендуется округлить до целого числа – 3
Затем определяем начало, середину и конец группы, для чего составляем таблицу. Прежде всего необходимо определить середину первой группы. Поскольку середина группы должна делиться без остатка на величину интервала, то соблюдая это требование, за середину первой группы следует взять варианту, равную 3. Середины других групп найдем следующим образом: от середины каждой предыдущей группы отнимают величину интервала. Так, если середина первой группы – 18.
Затем
найдем начало групп, для этого к ее
середине прибавляют величину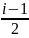 .
В нашем примере
.
В нашем примере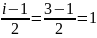 .
Прибавив 1 к середине первой группы
получим начало (19), а ее концом будет:
18-1=17.
.
Прибавив 1 к середине первой группы
получим начало (19), а ее концом будет:
18-1=17.
-
Начало группы
Середина группы
Конец группы
Варианты (V)
Частоты (p)
19
18
17
19-17
3
16
15
14
16-14
5
13
12
11
13-11
14
10
9
8
10-8
12
7
6
5
7-5
8
4
3
2
4-2
4
2. Проводим вычислениеMo, Me:
Mo – соответствует величине признака, которая чаще других встречается в данной совокупности.
Mo= 11 дней;
Me
– значение варианты, делящий вариационный
ряд пополам. При четном числе наблюдений
за медиану принимают среднюю величину
из двух центральных вариант. В нашем
примере четное число наблюдений
6,7,8,9,10,11,12,13 центральными вариантами
будут числа 9 и 10. Медиана в этом случае
равна:
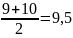 .
При нечетном числе наблюдений медианой
будет серединная (центральная) варианта,
которая определяется так:
.
При нечетном числе наблюдений медианой
будет серединная (центральная) варианта,
которая определяется так:
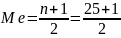 =13.
Это значит, что середина ряда приходится
на 13 порядковый номер варианты.
=13.
Это значит, что середина ряда приходится
на 13 порядковый номер варианты.
3. Проводим вычисление средней арифметической простой и взвешенной с использованием среднеарифметического способа.
-
Для простой М
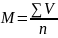
Для взвешенной М
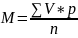
варианты не повторяются
варианты повторяются
V
P
V
p
V*p
2
1
2
5
10
3
1
3
1
3
4
1
4
3
12
5
1
5
1
5
6
1
6
2
12
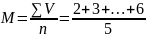 =4
=4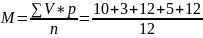 =3,5
=3,5
Затем проводим вычисление среднеарифметической взвешенной, для чего составляем следующую таблицу:
Таблица
Распределение длительности лечения больных ОРВИ в поликлинике в днях
№п/п |
V |
p |
V*p |
d(V-Mo) |
d2 |
d2*p |
1 |
2 |
1 |
2 |
-9 |
81 |
81 |
2 |
3 |
1 |
3 |
-8 |
64 |
64 |
3 |
4 |
2 |
8 |
-7 |
49 |
98 |
4 |
5 |
2 |
10 |
-6 |
36 |
72 |
5 |
6 |
3 |
18 |
-5 |
25 |
75 |
6 |
7 |
3 |
21 |
-4 |
16 |
48 |
7 |
8 |
3 |
24 |
-3 |
9 |
27 |
8 |
9 |
4 |
36 |
-2 |
4 |
16 |
9 |
10 |
5 |
50 |
-1 |
1 |
5 |
10 |
11 |
7 |
77 |
0 |
0 |
0 |
11 |
12 |
4 |
48 |
1 |
1 |
4 |
12 |
13 |
3 |
39 |
2 |
4 |
12 |
13 |
14 |
1 |
14 |
3 |
9 |
9 |
14 |
15 |
2 |
30 |
4 |
16 |
32 |
15 |
16 |
1 |
16 |
5 |
25 |
25 |
16 |
17 |
1 |
17 |
6 |
36 |
36 |
17 |
18 |
1 |
18 |
7 |
49 |
49 |
18 |
19 |
1 |
19 |
8 |
64 |
64 |
∑ |
189 |
45 |
450 |
- |
- |
717 |
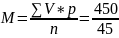 =10
дней.
=10
дней.
4. Проводим вычисление среднего квадратического отклонения (σ), которое позволяет судить о разнообразии признака в нашей статистической совокупности:
- d - истинное отклонение вариант от истинной средней;
σ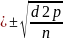 =
=
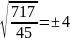 дня.
дня.
5. Определяем значение коэффициента вариации. Данный показатель является относительной мерой разнообразия признака, поскольку характеризует отношение среднего квадратического отклонения(σ) к средней арифметической величине (М), выраженное в процентах.
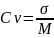 *
100=
*
100=
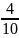 *
100= 40%
*
100= 40%
Для ориентировочной оценки степени разнообразия признака пользуются следующими критериями коэффициента вариации:
менее 10% - слабое разнообразие;
11-20% - среднее;
более 20% - сильное.
6. Проводим расчет средней ошибки средней арифметической величины (mM), которая является объективным показателем репрезентативности (представительности). Ошибка репрезентативности(mM) является важным статистическим показателем, который необходим для оценки достоверности результатов исследования.
mM=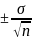 =
=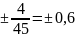 .
.
Необходимо
отметить, при проведении биомедицинских
исследований значение показателя
М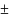 mMрассматривается
как показатель физиологической нормы.
mMрассматривается
как показатель физиологической нормы.
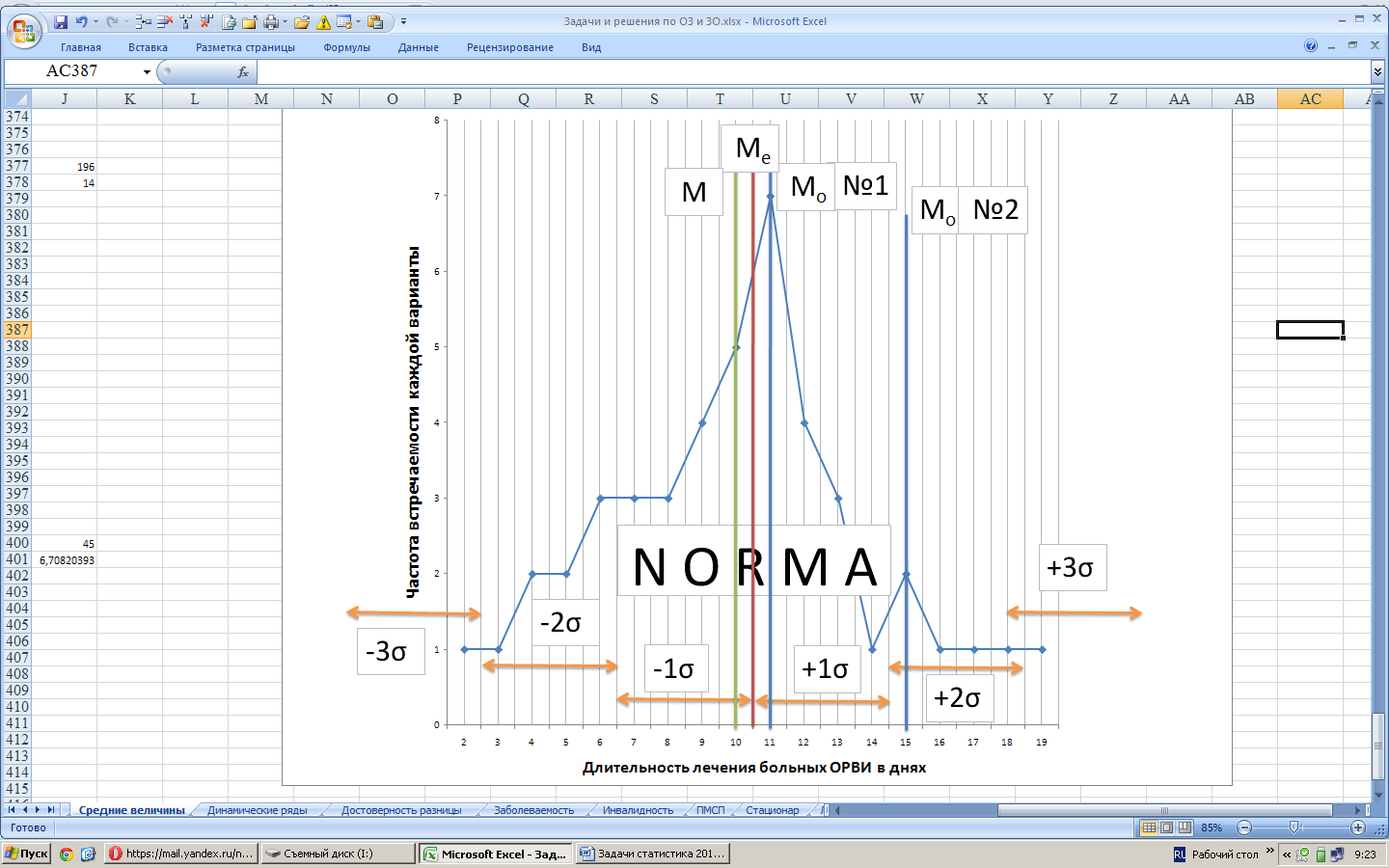
Рис.1.Распределение длительности лечения больных ОРВИ в поликлинике в днях
Выводы.
1.Распределение длительности лечения больных ОРВИ в поликлинике имеет ассиметричный характер, смещение влево.
2.Разнообразие признака сильное с учетом значения коэффициента вариации.
