
Решение эталонной задачи
Требуется:
1. Вычислить стандартизованные показатели, используя прямой метод стандартизации.
2. Сравнить:
Общие показатели, рассчитанные обычным способом;
Частные показатели в отдельных группах;
Стандартизованные и обычные показатели.
3. Сделать вывод, вытекающий из сопоставления обычных стандартизованных показателей в сравниваемых группах.
Распределение населения города А и Б по возрасту и числу умерших (в абсолютных числах)
Возраст в годах |
Город А |
Город Б |
1 этап |
2 этап |
3 этап |
|||||||
число жителей |
из них умерло |
число жителей |
из них умерло |
% умерших |
«ожидаемое число» |
|||||||
А |
Б |
стандарт |
А |
Б |
||||||||
0-14 |
3000 |
30 |
1000 |
10 |
1,0 |
1,0 |
4000 |
40 |
40 |
|||
15-49 |
5000 |
10 |
5000 |
10 |
0,2 |
0,2 |
10000 |
20 |
20 |
|||
50 и старше |
2000 |
60 |
4000 |
120 |
3,0 |
3,0 |
6000 |
180 |
180 |
|||
Всего |
10000 |
100 |
10000 |
140 |
1,0 |
1,4 |
20000 |
240 |
240 |
|||
4 этап |
|
|
|
|||||||||
На 1 этапе стандартизации требуется определить, в каких возрастных группах выше показатель смертности. Для этого вычисляют специальные интенсивные показатели, т.е. процент смертности отдельно для всех возрастных групп. Расчет ведется следующим образом:
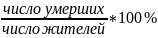
Получившиеся показатели записываем в таблицу. Следует проанализировать интенсивные показатели по городу А и Б. Из таблицы видно, что в целом (в строке «Всего») в городе Б показатель смертности выше, чем в городе А. Однако, показатели по всем выделенным возрастным группам на имеют отличий. Следовательно, в данном случае различие в общих итоговых интенсивных показателях, полученных по городам, может быть связано с неоднородностью возрастного состава населения в этих городах. Для элиминирования (устранения) косвенного влияния на показатели смертности разного состава жителей по возрасту необходимо провести стандартизацию.
2 этап. Выбор и расчет стандарта. За стандарт следует принимать тот состав совокупностей, в котором отразились бы все особенности состава сравниваемых групп. В нашем примере за такой стандарт принята суммарная численность жителей города А и Б. Стандартом для возрастной группы 0-14 лет – 4000 (3000+1000), для 15-49 лет – 10000 (5000+5000), для 50 и старше – 6000 (2000+4000). Общее число жителей в двух городах составит – 20000. Зная интенсивные показатели (1 этап) и стандарт (2 этап), можно перейти к 3 этапу.
3 этап. Определение «ожидаемых чисел» умерших в каждой группе стандарта. Порядок вычисления можно показать на следующем примере. В городе А, умерших в возрастной группе 0-14 лет - 1,0%. Сколько было бы умерших среди 4000 жителей? Составим пропорцию и произведем расчет:
100 – 1,0%
4000 - x
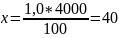
Таким образом, 40 – «ожидаемое число» умерших в возрастной группе 0-14, из 4000 жителей группы стандарта. Аналогичные расчеты проведем по другим возрастным группам городов А и Б. Данные запишем в таблицу.
4 этап. Определение стандартизованных показателей. Просуммировав абсолютные «ожидаемые» числа умерших в разных возрастных группах по каждому городу отдельно, полученные суммы относят к общей численности жителей, указанной в итоговой строке стандарта. Это отношение выражают в процентах и получают стандартизованные показатели. Так, в городе А сумма «ожидаемых» чисел, умерших составит: 40+20+180=240. Стандартизованный показатель умерших в городе А равен:
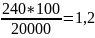
Для города Б сумма «ожидаемых» чисел умерших будет аналогична.
5 этап. Сравнение умерших в разных возрастных группах городов А и Б по стандартизованным и общим интенсивным показателям. Для этого следует выписать стандартизованные и интенсивные показатели в отдельную аналитическую таблицу, сопоставить эти данные и сделать общий вывод.
Сопоставление уровней смертности в городах А и Б
Показатели |
город А |
город Б |
Результаты сравнения |
Стандартизованные |
1,2 |
1,2 |
А=Б |
Общие интенсивные (грубые) |
1,0 |
1,4 |
А≥Б |
Вывод. Сравнение стандартизованных показателей, рассчитанных для жителей городов А и Б, позволяет сделать заключение, что при одинаковом составе жителей по возрасту в городах А и Б показатель смертности одинаковый. А при сравнении общих (грубых) интенсивных показателей результаты получились немного другие: в городе Б показатель смертности выше, чем в городе А, в связи с тем, что на общие (интенсивные) показатели оказал влияние разный состав жителей по возрасту в этих городах.
