лаб 4 / лаба 4

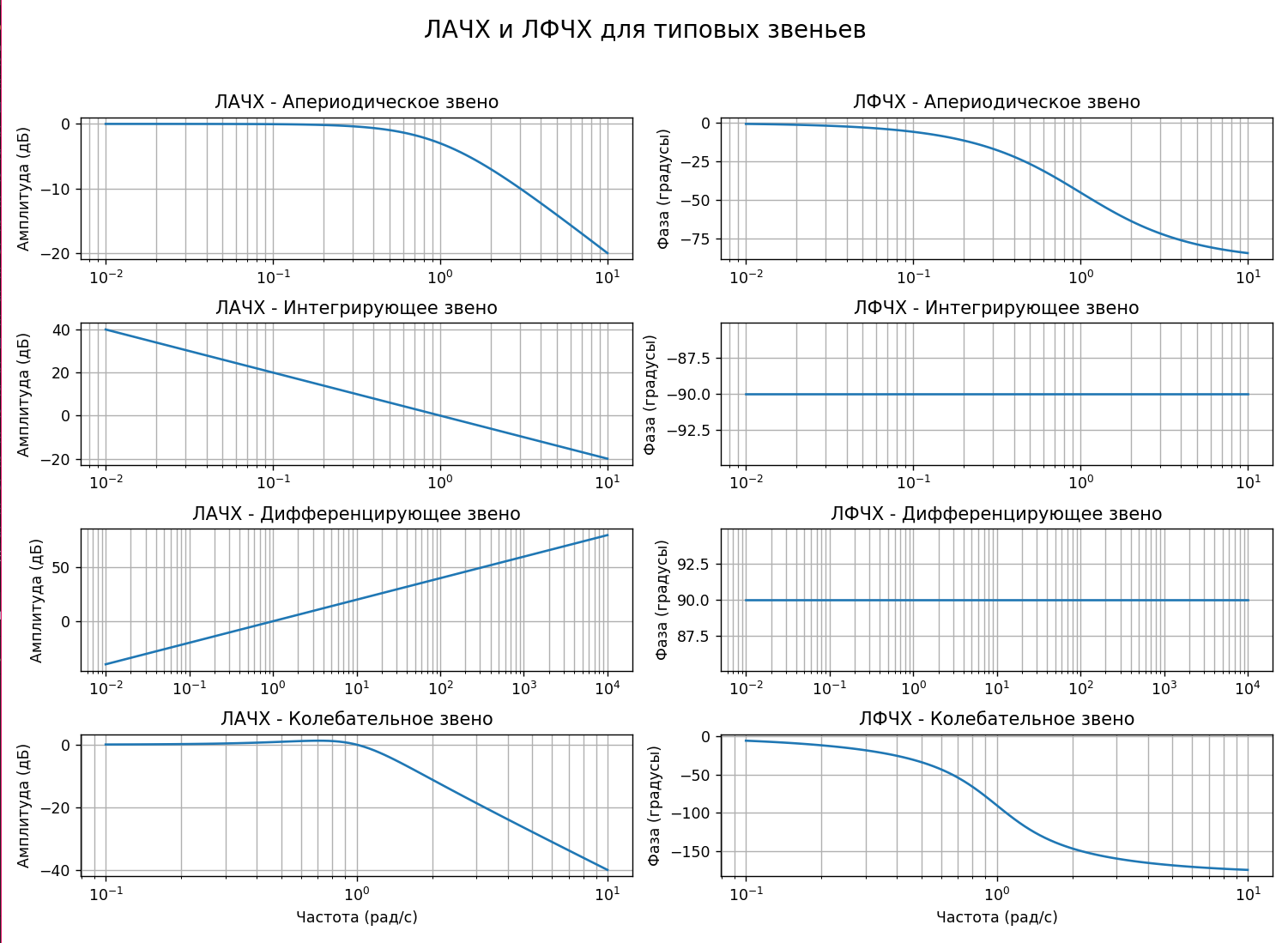
Апериодическое звено:

• ЛАЧХ: График амплитудно-частотной характеристики (ЛАЧХ) показывает спад амплитуды при увеличении частоты. Это поведение типично для апериодического звена, у которого амплитуда уменьшается с ростом частоты.

• ЛФЧХ: Фазово-частотная характеристика (ЛФЧХ) показывает, что фаза смещается от 0 градусов к -90 градусам по мере увеличения частоты.

Интегрирующее звено:

• ЛАЧХ: Амплитуда линейно уменьшается с ростом частоты на -20 дБ/декаду. Это связано с тем, что интегрирующее звено действует как фильтр нижних частот.

• ЛФЧХ: Фаза остаётся примерно на уровне -90 градусов на всём диапазоне частот, что соответствует постоянному фазовому сдвигу интегрирующего звена.

Дифференцирующее звено:

• ЛАЧХ: Амплитуда увеличивается на +20 дБ/декаду с ростом частоты, так как дифференцирующее звено усиливает высокочастотные составляющие.

• ЛФЧХ: Фаза сохраняется на уровне +90 градусов по всему диапазону частот, что характерно для дифференцирующего звена.

Колебательное звено:

• ЛАЧХ: График амплитудной характеристики имеет спад с ростом частоты после пика. Поведение напоминает колебательное звено второго порядка, где амплитуда сначала увеличивается, достигает пика и затем снижается.

• ЛФЧХ: Фазовая характеристика начинается с 0 градусов и постепенно снижается, достигая -180 градусов при более высоких частотах, что отражает фазовый сдвиг в колебательных системах.

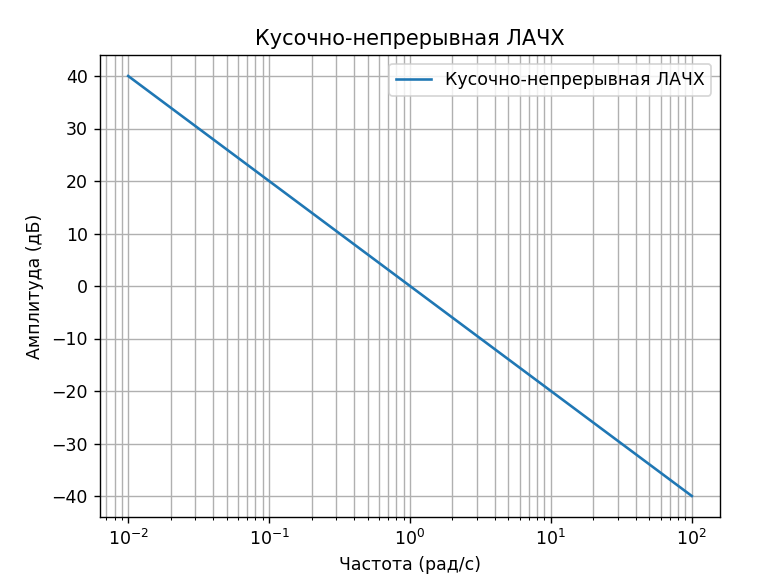
import numpy as np import matplotlib.pyplot as plt from scipy import signal # Функции для создания типовых звеньев def aperiodic_element(T): return signal.TransferFunction([1], [T, 1]) def integrator(): return signal.TransferFunction([1], [1, 0]) def differentiator(): return signal.TransferFunction([1, 0], [1]) def second_order_system(omega_n, zeta): return signal.TransferFunction([omega_n ** 2], [1, 2 * zeta * omega_n, omega_n ** 2]) # Функция для построения ЛАЧХ и ЛФЧХ для всех звеньев на одной странице def plot_all_bode(T_aperiodic, omega_n, zeta): # Задание параметров системы systems = [ (aperiodic_element(T_aperiodic), "Апериодическое звено"), (integrator(), "Интегрирующее звено"), (differentiator(), "Дифференцирующее звено"), (second_order_system(omega_n, zeta), "Колебательное звено") ] # Настройка графиков fig, axs = plt.subplots(len(systems), 2, figsize=(12, 10)) fig.suptitle('ЛАЧХ и ЛФЧХ для типовых звеньев', fontsize=16) # Построение ЛАЧХ и ЛФЧХ для каждого звена for i, (system, title) in enumerate(systems): w, mag, phase = signal.bode(system) # ЛАЧХ axs[i, 0].semilogx(w, mag) axs[i, 0].set_title(f'ЛАЧХ - {title}') axs[i, 0].set_ylabel('Амплитуда (дБ)') axs[i, 0].grid(True, which="both") # ЛФЧХ axs[i, 1].semilogx(w, phase) axs[i, 1].set_title(f'ЛФЧХ - {title}') axs[i, 1].set_ylabel('Фаза (градусы)') axs[i, 1].grid(True, which="both") for ax in axs[-1, :]: # Установить подпись оси X только для нижних графиков ax.set_xlabel('Частота (рад/с)') plt.tight_layout(rect=[0, 0.03, 1, 0.95]) plt.show() # Построение линейной кусочно-непрерывной ЛАЧХ frequencies = np.logspace(-2, 2, 100) linear_mag = -20 * np.log10(frequencies) # Пример линейного аппроксимированного ЛАЧХ plt.figure() plt.semilogx(frequencies, linear_mag, label="Кусочно-непрерывная ЛАЧХ") plt.xlabel("Частота (рад/с)") plt.ylabel("Амплитуда (дБ)") plt.title("Кусочно-непрерывная ЛАЧХ") plt.legend() plt.grid(True, which="both") plt.show() # Задание параметров системы T_aperiodic = 1.0 # Параметр апериодического звена omega_n = 1.0 # Собственная частота колебательного звена zeta = 0.5 # Коэффициент демпфирования # Построение всех графиков plot_all_bode(T_aperiodic, omega_n, zeta)