лаб 3 / Laboratornaya_rabota_3

Добавил:

vadikbee ИВТ (советую зайти в "Несортированное") Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

Основы Теории Управления

Файл:

мнимой полуосью. ЛФЧХ параллельна оси частот и проходит на уровне

т.е. сдвиг фазы не зависит от частоты и равен

. ЛАЧХ есть прямая,

т.е. сдвиг фазы не зависит от частоты и равен

. ЛАЧХ есть прямая,

.pdf

Скачиваний:

Добавлен:

13.11.2024

Размер:

853.21 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Национальный исследовательский университет «МИЭТ»

Лабораторная работа №3. Исследование элементарных звеньев и построение их

характеристик.

Москва 2024

Цель работы.

1.Ознакомиться с временными и частотными характеристиками типовых

звеньев.

2.Получить практические навыки построения характеристик в среде

MatLab.

Теоретическая часть

Звено – математическая модель элемента, соединения элементов или любой части системы. Звенья, как и системы, могут описываться дифференциальными уравнениями довольно высокого порядка, и в общем случае их передаточные функции могут быть записаны в виде:

m 1

... b

W (s)

n 1

... a



( 1 )

Их всегда можно представить как соединение типовых или элементарных звеньев, порядок дифференциальных уравнений которых не выше второго.

Из курса алгебры известно, что полином произвольного порядка можно разложить на простые множители – множители вида:

k	s; d	s d		; d	s	2	d		s d
						2
1	1		2	1				2		3

Следовательно, передаточную функцию (1) можно представить произведение простых множителей вида (2) и простых дробей вида:

;

s d

( 2 )

как

( 3)

Звенья, передаточные функции которых имеют вид простых множителей, называют типовыми или элементарными звеньями.

В дальнейшем будем рассматривать звенья соответственно обозначениям, указанным на рисунке:

Рисунок – Принятые обозначения

Пропорциональное звено

вида

Пропорциональным называют звено, которое описывается уравнением x t k u t или передаточной функцией W s k .

Частотные характеристики этого типового звена имеют вид:

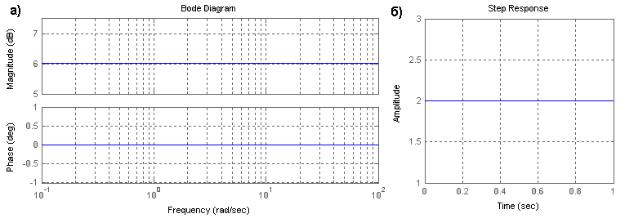
W jw k; U k; V 0; A k;0; L 20 lg k;

Временные характеристики этого типового звена имеют вид:

h t k 1 t ; w t t ;

Рисунок 1 – Характеристики пропорционального звена, при к=2 На рисунке 1 представлены логарифмические частотные и переходная

характеристики пропорционального звена при k=2.

Интегрирующее звено
Интегрирующим называют звено, которое				описывается уравнением
s x k u или передаточной функцией W s	k	.
s x k u или передаточной функцией W s		.
	s
Частотная передаточная функция W jw			k	jk	.
Частотная передаточная функция W jw			j		.
			j

Остальные характеристики имеют вид:

U 0;
V		k	;
V			;

A	k	;
A		;

			;
		2	;
		2
L 20 lg k 20 lg ;

Временные характеристики имею вид: h t k t; w t k;

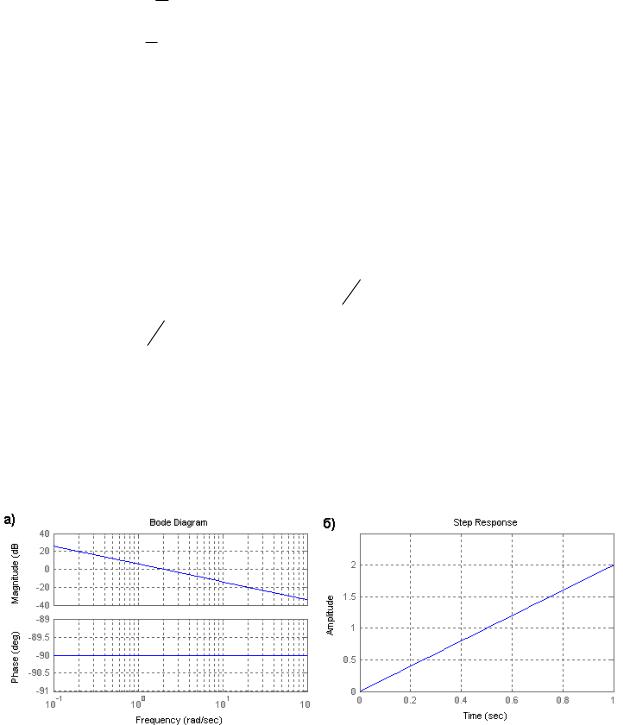
Амплитудно-фазовая частотная характеристика интегрирующего звена совпадает с отрицательной мнимой полуосью. ЛФЧХ (рисунок 2а) параллельна

оси частот	и проходит на			уровне	2	;	т.е. сдвиг фазы	не	зависит от


частоты и равен –			. ЛАЧХ (рисунок 2а) – наклонная прямая, проходящая через
		2

точку с	координатами			1; L 20 lg k .			Как видно	из	уравнения
L 20 lg k 20 lg ,			при увеличении частоты				на одну декаду ордината L

уменьшается на 20 дБ. Поэтому наклон ЛАЧХ равен –20 дБ/дек. Переходная характеристика представляет собой прямую, проходящую через начало координат с угловым коэффициентом наклона, равным k (рисунок 2б).

Рисунок 2 – Характеристики интегрирующего звена при k=2

Дифференцирующее звено

Дифференцирующим называют звено, которое описывается уравнением x k s u или передаточной функцией W s k s .

Частотные характеристики имеют вид:

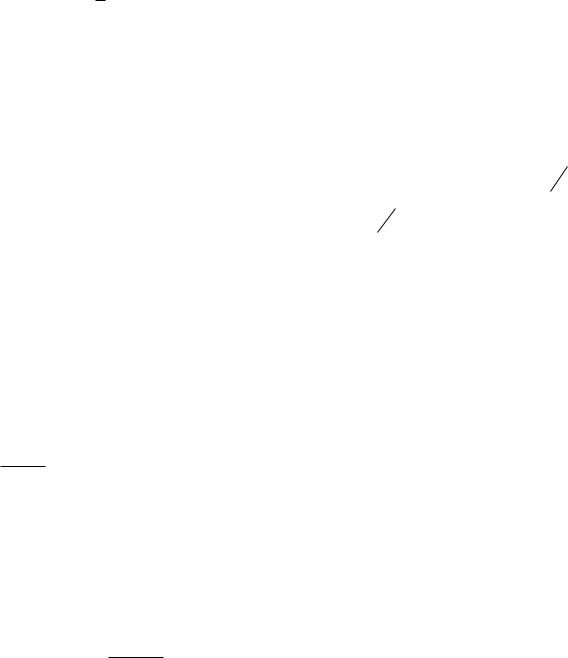
W j jk ;
U ω 0;
V k ;
A ω k ;
ω	π	;
	2

L ω 20lg k 20lg ;

Временные характеристики имеют вид:

h t δ t ;

ω t δ t ;

Амплитудно-фазовая частотная характеристика совпадает с положительной

проходящая через точку с координатами 1 и L 20 lg k и имеющая наклон

20 дБ/дек; L увеличивается на 20 дБ/дек при увеличении частоты на одну декаду.

Апериодическое звено

Апериодическим звеном первого порядка называют звено, которое описывается уравнением T s 1 y k u (4) или передаточной функцией

W s	k		.
W s	Ts 1		.
	Ts 1
	Это	звено также называют инерционным звеном

Апериодическое звено в отличие от рассмотренных

характеризуется двумя параметрами: постоянной времени	T
коэффициентом k .
Частотная передаточная функция:

первого порядка. выше звеньев и передаточным

W j	k	;
	Tj 1

Умножив числитель и знаменатель на комплексно-сопряженное знаменателю число, получим частотные характеристики:

U ω k ;

Tω 2 1

V ω kTω ;

Tω 2 1

Амплитудную и фазовую частотные функции можно определить,

воспользовавшись правилом модулей и аргументов.
Так как модуль числителя частотной передаточной функции равен	k , а

модуль знаменателя

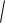T 2

1 , то
A	k
A	2
	2	1
	T	1

( 5 )

Аргумент числителя W j равен нулю, а аргумент знаменателя поэтому ω arg W jω arctg ωT .

arctg T

С учетом уравнения (5) получим:
		L ω 20 lg A ω 20 lg k 20 lg
		L ω 20 lg A ω 20 lg k 20 lg		Tω 2 1	( 6 )
При	1	в сумме	2
При	T	в сумме	Tω 1 первым слагаемым можем пренебречь и
	T
выражение (6) примет вид:			L 20 lg k , т.е. это прямая линия, параллельная

оси абсцисс.

При

		1
		T
		T

в сумме

Tω	1
2

можем пренебречь 1, тогда выражение (6)

примет вид:	2	20 lg k 20 lg T , как видно
	L ω 20 lg A ω 20 lg k 20 lg Tω
из этого уравнения, при увеличении частоты на		одну декаду ордината	L
уменьшается на 20 дБ. Поэтому наклон ЛАЧХ равен –20 дБ/дек.
Таким	образом, асимптотическую ЛАЧХ	можем представить в	виде

соединяющихся в точке

		1
		T
		T

двух линий: слева – параллельной оси абсцисс, а

справа – идущей с наклоном –20 дБ/дек.

Частоту, на которой ЛАЧХ меняет наклон, будем называть сопрягающей.

Вычислим истинное

значение ЛАЧХ

на сопрягающей

частоте:

L c

|k 1 20 lg 1 20 lg T

1 20 lg 2 3 дБ ,

т.е.

истинное

значение

характеристики меньше асимптотического на 3 дБ.

Решив дифференциальное уравнение (4) при

u 1 t

и нулевом начальном

t T

условии, получим h t k 1

. Весовая функция

t h t

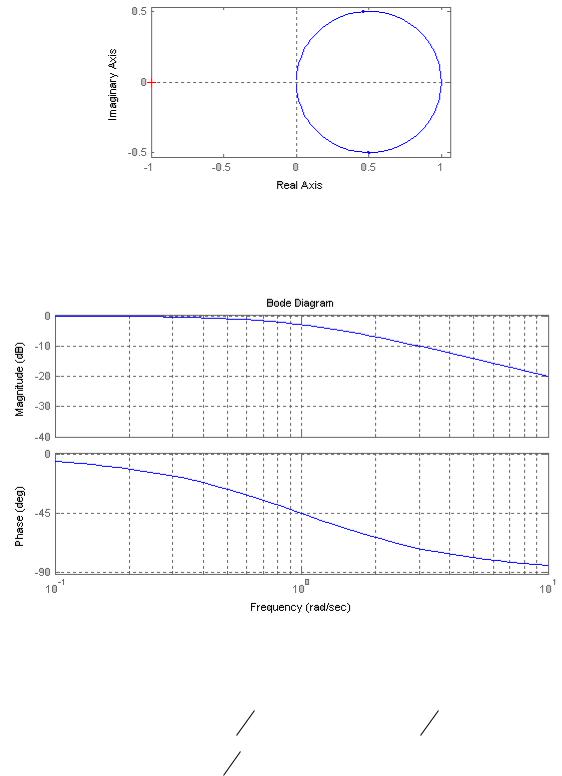
Рисунок 3 – АФЧХ апериодического звена, при Т=1, к=1 АФЧХ апериодического звена (рисунок 3) есть окружность, в чем нетрудно

убедиться, исключив из параметрических уравнений АФЧХ частоту.

Рисунок – 4 Логарифмические характеристики апериодического звена при Т=1, к=1 Логарифмические частотные характеристики представлены на рис. 4. Логарифмическая фазовая частотная характеристика асимптотически

стремится к нулю при

и к 2

при

. При 1T фазовая частотная

функция принимает значение

. ЛФЧХ всех апериодических звеньев имеют

одинаковую форму и могут быть получены по какой-либо одной характеристики параллельным сдвигом вдоль оси частот влево или вправо в зависимости от постоянной времени T .

Переходная характеристика апериодического звена (рисунок 5а) представляет собой экспоненциальную кривую. По ней можно определить

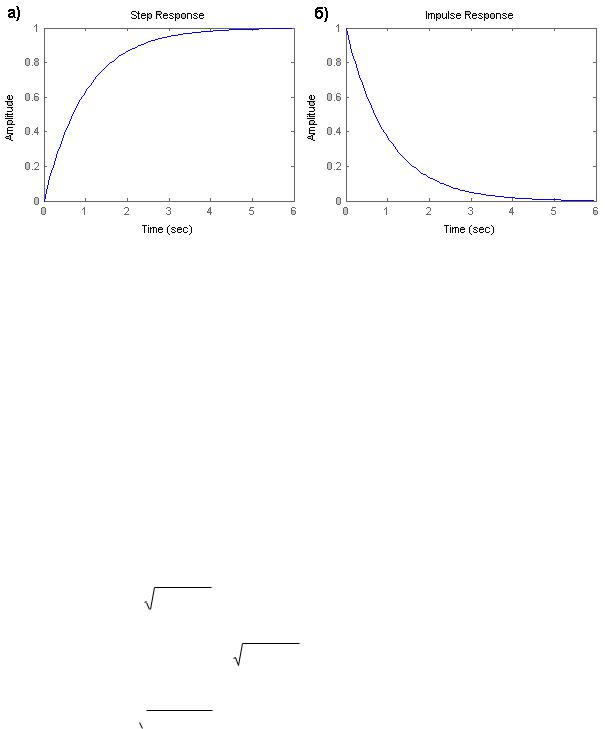
следующие параметры: передаточный коэффициент, равный установившемуся значению h ; постоянную времени Т и другие характеристики.

Импульсная переходная характеристика представлена на рисунке 5б.

Рисунок 5 – Временные характеристики апериодического звена

Форсирующее звено.

Форсирующим звеном, или форсирующим звеном первого порядка

называют звено, которое описывается уравнением

x k T s 1 u

или

передаточной функцией W s k T s 1 .

Это звено, как и апериодическое, характеризуется двумя параметрами: постоянной времени T и передаточным коэффициентом k .

Частотная передаточная функция:

W j

k Tj

;

Остальные частотные характеристики имеют вид:

U ω k, V ω kTω;
2
A ω k Tω 1;
ω arctg T ω ;
L ω 20 lg k 20 lg	2	1;
L ω 20 lg k 20 lg	Tω	1;

Временные характеристики имеют вид:

h t k 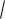Tδ t 1 t ; w t k Tδ t 1 t ;

АФЧХ есть прямая, параллельная мнимой оси и пересекающая действительную ось в точке U k . Как и в случае апериодического звена, на практике ограничиваются построением асимптотической ЛАЧХ.

Уравнение асимптотической ЛАЧХ форсирующего звена:

20 lg k	при ω 1		,

L ω	T
	T
20 lg k 20 lg T		при ω		1
				T
				T
ЛФЧХ форсирующего звена			можно	получить зеркальным отражением

относительно оси частот ЛФЧХ апериодического звена.

Колебательное, консервативное и апериодическое второго порядка звенья.

Звено, которое можно описать уравнением

T	2	s T s 1 x
	2
0		1

, или в другой

форме

T	2	s	2

2 Ts 1 x

, где

T T	,
0

		T
		1	2T
		1

, или передаточной функцией

W s	T				k	, называют колебательным при
		2	s	2	2 Ts 1


0 T1 0 , и апериодическим второго порядка

называют коэффициентом демпфирования.

0 1, консервативным при при 1. Коэффициент

Колебательное звено (

Частотная передаточная функция

W j			k
	T		j2 T
1		2
	2

Умножив числитель и знаменатель на комплексно-сопряженное знаменателю выражение, получим вещественную и мнимую частотные функции:

U		k 1 T					2	2

	1 T	2		2	2				2	;


							2 T
V	1 T		2k T							;
		2		2	2				2


							2 T
Фазовая частотная функция,
монотонно от 0 до						и выражается

как это видно из АФЧХ (рис. 6), изменяется формулой

	arctg		2T				, при			1
	arctg			2		2	, при			1
	1	T		2		2				T ,
	1	T								T ,		.
			2T									.
arctg			2T						, при		1
arctg			1 T						, при		1
			1 T		2			2			T.
					2			2

Логарифмическая фазовая частотная характеристика (рис. 6) при асимптотически стремится к оси частот, а при - к прямой .

Амплитудная частотная функция

A	k	,


	1 T 2 2 2 2 T 2

ЛАЧХ имеет вид:

		2	2	2		2
L 20 lg k 20 lg	1 T				2 T

Рисунок 6 – Частотные характеристики колебательного звена при Т=1; 2*ksi*T=0.3 Переходная функция:

Весовая функция:

sin βt

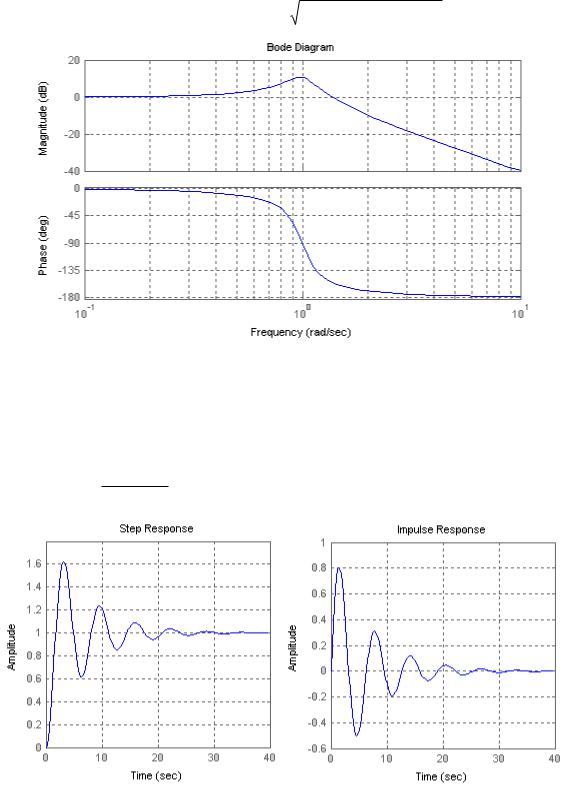
Рисунок 7 – Временные характеристики колебательного звена при Т=1; 2*ksi*T=0.3 По переходной характеристике (рисунок 7) можно определить параметры

колебательного звена следующим образом:

Консервативное звено ( 0 ).

Передаточная функция

1 / 21 2 > Следующая >>>

Соседние файлы в папке лаб 3

#
13.11.2024853.21 Кб14Laboratornaya_rabota_3.pdf
#
13.11.20241.76 Mб17лаба3.docx