
лаб 3 / лаба3
.docxВходные данные:

![]()
Параметр k — коэффициент усиления:
Параметр T — время постоянной системы:
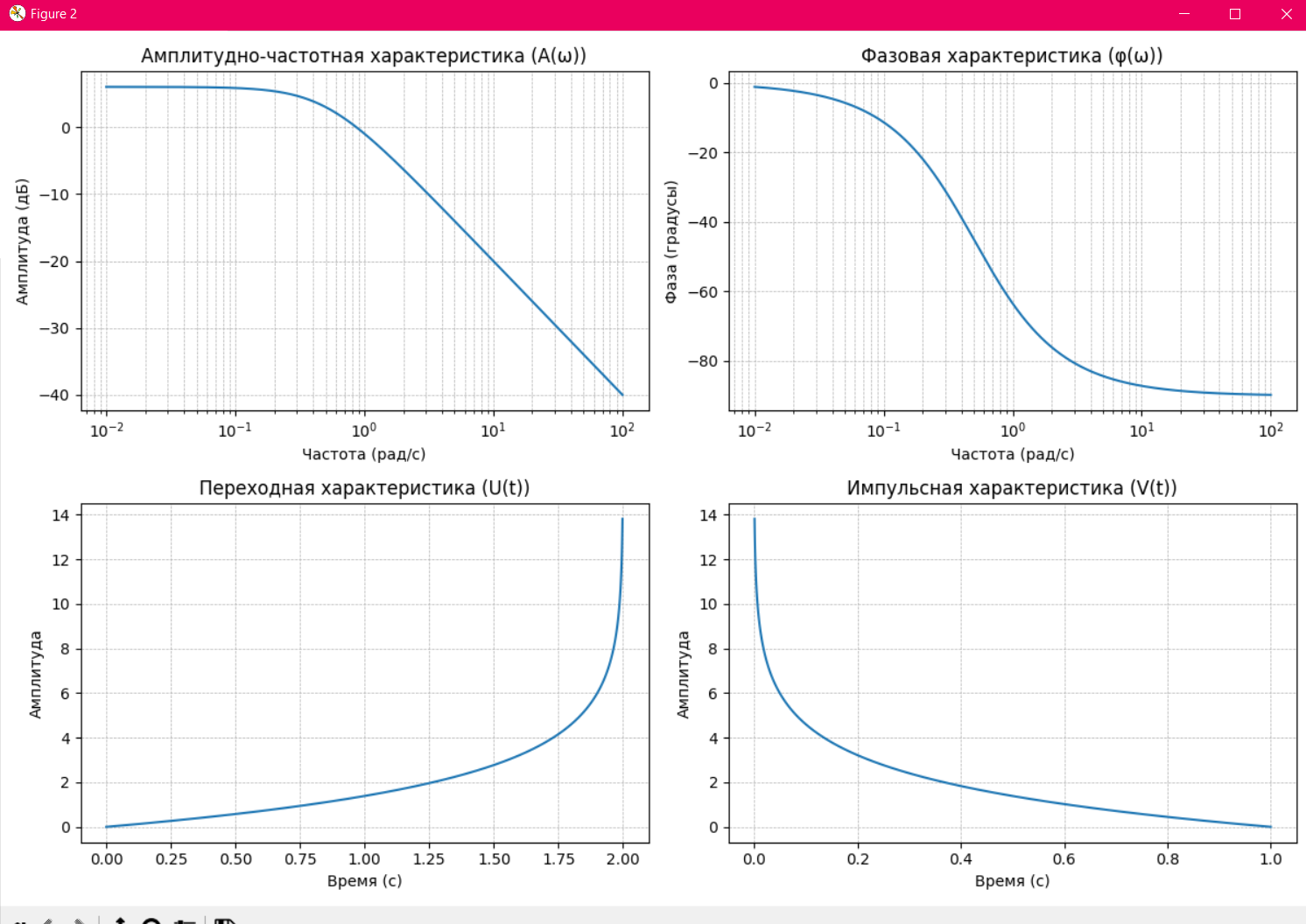
Амплитудно-частотная характеристика
Этот график (в верхнем левом углу) показывает, как амплитуда выходного сигнала изменяется в зависимости от частоты входного сигнала.
На низких частотах система пропускает сигнал почти без ослабления, и амплитуда остается около нуля дБ.
По мере увеличения частоты амплитуда начинает падать с уклоном примерно −20-20−20 дБ/дек, что характерно для апериодического звена первого порядка.
Это поведение указывает на то, что система действует как фильтр, ослабляя высокочастотные компоненты входного сигнала.
Фазовая
Этот график (в верхнем правом углу) показывает, как фазовый сдвиг изменяется с частотой.
На низких частотах фазовый сдвиг близок к 0 градусам, что означает, что система практически не задерживает сигнал по фазе.
С увеличением частоты фазовый сдвиг постепенно достигает -90 градусов, что типично для апериодического звена первого порядка.
Этот фазовый сдвиг означает, что при высоких частотах выходной сигнал задерживается на четверть периода относительно входного сигнала.
Переходная характеристика
Этот график (в нижнем левом углу) показывает отклик системы на единичный скачок (ступенчатый сигнал) во времени.
В начале система быстро реагирует на изменение входного сигнала и начинает нарастать по экспоненциальной зависимости.
Со временем амплитуда стремится к конечному значению, определенному коэффициентом усиления kkk. Этот график описывает, как система устанавливается при подаче постоянного входного сигнала.
Импульсная характеристика
Этот график (в нижнем правом углу) показывает отклик системы на единичный импульс.
В начале амплитуда имеет максимальное значение, затем экспоненциально убывает, стремясь к нулю.
Импульсная характеристика показывает, как система реагирует на мгновенное воздействие, затухая со временем. Эта характеристика важна для оценки того, как быстро система успокаивается после кратковременного возмущения
Bode plot
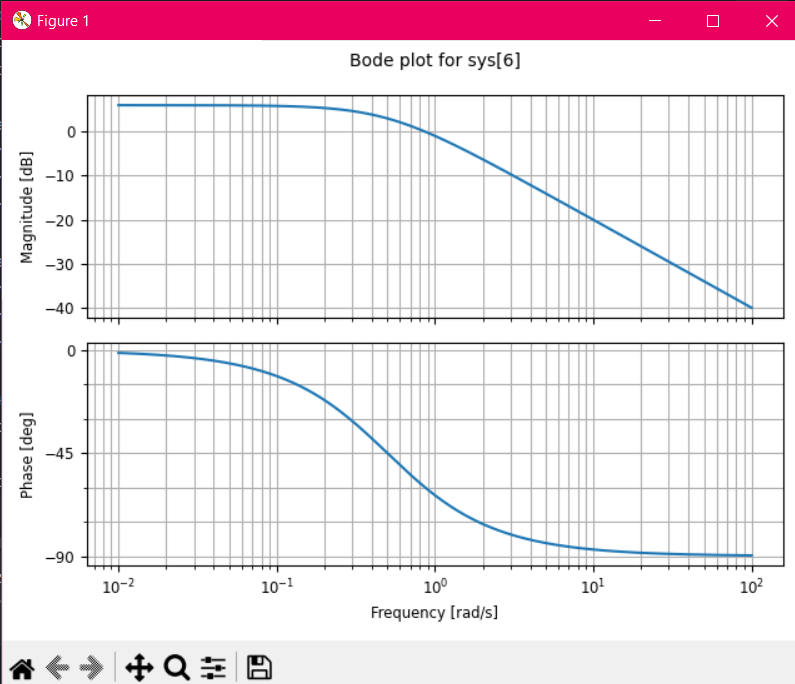
Bode plot отличается от обычного графика частотных характеристик тем, что он представляет амплитуду и фазу сигнала на логарифмической шкале по частоте
Верхний график — амплитудно-частотная характеристика (АЧХ):
Отображает зависимость амплитуды (в децибелах) от частоты (в логарифмическом масштабе).
Чем выше частота, тем сильнее система ослабляет сигнал, что типично для апериодического звена.
Нижний график — фазовая характеристика (ФЧХ):
Показывает фазовый сдвиг (в градусах) в зависимости от частоты.
На низких частотах фазовый сдвиг близок к нулю, а по мере увеличения частоты фазовый сдвиг стремится к -90 градусам.
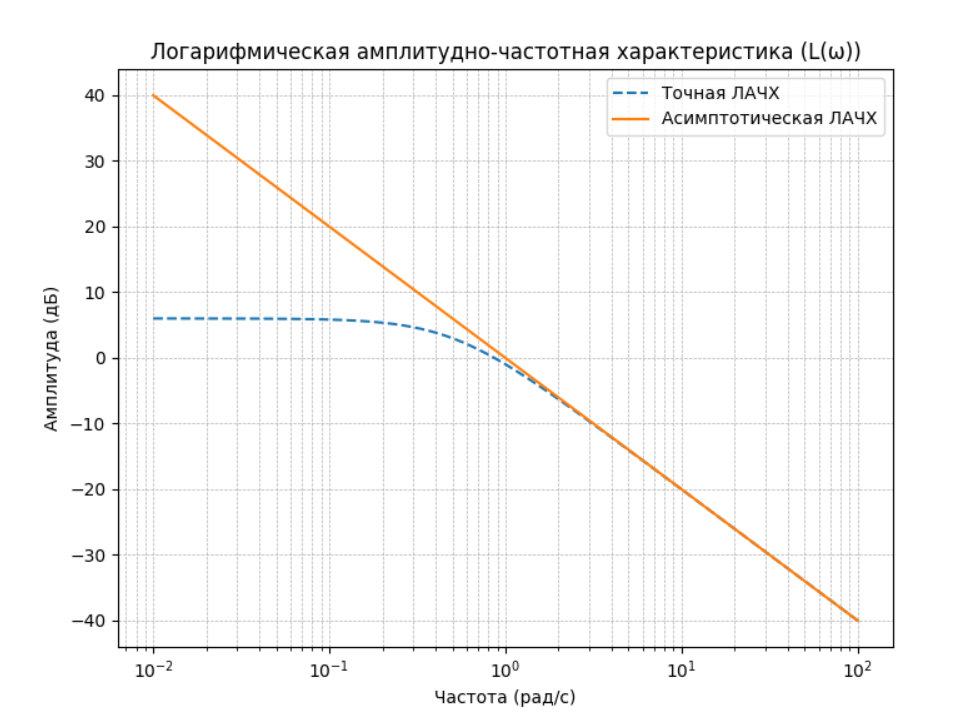
Изучить влияние параметра Т на вид () и L(). Сделать выводы.
Параметр T определяет инерционность системы:
Чем больше T, тем более инерционной становится система. Она реагирует медленнее на частотные изменения, что проявляется в виде плавного спада амплитуды на ЛАЧХ и увеличенного фазового сдвига при более низких частотах.
Фазовый сдвиг и амплитудный отклик:
Увеличение T сдвигает фазу системы на более низких частотах и задерживает реакцию на частотные изменения. Это делает систему менее восприимчивой к высокочастотным сигналам и подходит для фильтрации шумов.
2) Построить в одном окне асимптотическую и точную ЛАЧХ апериодического звена. Сделать выводы.
Построение асимптотической и точной ЛАЧХ на одном графике позволяет видеть, как апериодическое звено реагирует на разные частоты. Асимптотическая характеристика дает общее представление о системе, в то время как точная характеристика показывает реальные переходные эффекты. При проектировании и анализе систем управления можно использовать асимптотическую ЛАЧХ для быстрого качественного анализа, но для точной оценки поведения системы, особенно в переходных режимах, лучше использовать точную ЛАЧХ.
Код
import numpy as np import matplotlib.pyplot as plt from control.matlab import tf, step, impulse, bode from tkinter import Tk, Label, Entry, Button def build_transfer_function(k, T): # Создание передаточной функции апериодического звена return tf([k], [T, 1]) def plot_characteristics(k, T): # Создаем передаточную функцию sys = build_transfer_function(k, T) # Частотный диапазон для построения АЧХ и ФЧХ w = np.logspace(-2, 2, 1000) # Вычисление амплитудно-частотной и фазовой характеристик mag, phase, omega = bode(sys, w) # Построение графиков fig, axs = plt.subplots(2, 2, figsize=(12, 8)) # Амплитудная характеристика (A(ω)) axs[0, 0].semilogx(omega, 20 * np.log10(mag)) axs[0, 0].set_title("Амплитудно-частотная характеристика (A(ω))") axs[0, 0].set_xlabel("Частота (рад/с)") axs[0, 0].set_ylabel("Амплитуда (дБ)") axs[0, 0].grid(True, which="both", linestyle="--", linewidth=0.5) # Фазовая характеристика (φ(ω)) axs[0, 1].semilogx(omega, np.degrees(phase)) axs[0, 1].set_title("Фазовая характеристика (φ(ω))") axs[0, 1].set_xlabel("Частота (рад/с)") axs[0, 1].set_ylabel("Фаза (градусы)") axs[0, 1].grid(True, which="both", linestyle="--", linewidth=0.5) # Переходная характеристика (U(t)) t, y = step(sys) axs[1, 0].plot(t, y) axs[1, 0].set_title("Переходная характеристика (U(t))") axs[1, 0].set_xlabel("Время (с)") axs[1, 0].set_ylabel("Амплитуда") axs[1, 0].grid(True, linestyle="--", linewidth=0.5) # Импульсная характеристика (V(t)) t, y = impulse(sys) axs[1, 1].plot(t, y) axs[1, 1].set_title("Импульсная характеристика (V(t))") axs[1, 1].set_xlabel("Время (с)") axs[1, 1].set_ylabel("Амплитуда") axs[1, 1].grid(True, linestyle="--", linewidth=0.5) plt.tight_layout() plt.show() # Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) - Точная и Асимптотическая plt.figure(figsize=(8, 6)) # Точная ЛАЧХ plt.semilogx(omega, 20 * np.log10(mag), label="Точная ЛАЧХ", linestyle='--') # Асимптотическая ЛАЧХ asymptotic_mag = 20 * np.log10(k) - 20 * np.log10(omega * T) plt.semilogx(omega, asymptotic_mag, label="Асимптотическая ЛАЧХ", linestyle='-') plt.title("Логарифмическая амплитудно-частотная характеристика (L(ω))") plt.xlabel("Частота (рад/с)") plt.ylabel("Амплитуда (дБ)") plt.legend() plt.grid(True, which="both", linestyle="--", linewidth=0.5) plt.show() def start_plotting(): # Получение значений параметров из полей ввода k = float(entry_k.get()) T = float(entry_T.get()) plot_characteristics(k, T) # Создание окна интерфейса root = Tk() root.title("Построение характеристик апериодического звена") Label(root, text="Введите значение k:").grid(row=0, column=0) entry_k = Entry(root) entry_k.grid(row=0, column=1) entry_k.insert(0, "3") # Предустановленное значение k Label(root, text="Введите значение T:").grid(row=1, column=0) entry_T = Entry(root) entry_T.grid(row=1, column=1) entry_T.insert(0, "2") # Предустановленное значение T # Кнопка для построения графиков Button(root, text="Построить графики", command=start_plotting).grid(row=2, column=0, columnspan=2) root.mainloop()

k=3
T=2 (так как мы использовали его значение ранее)
ξ=0.03
Для колебательного звена передаточная функция будет иметь вид:
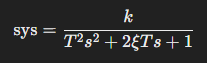
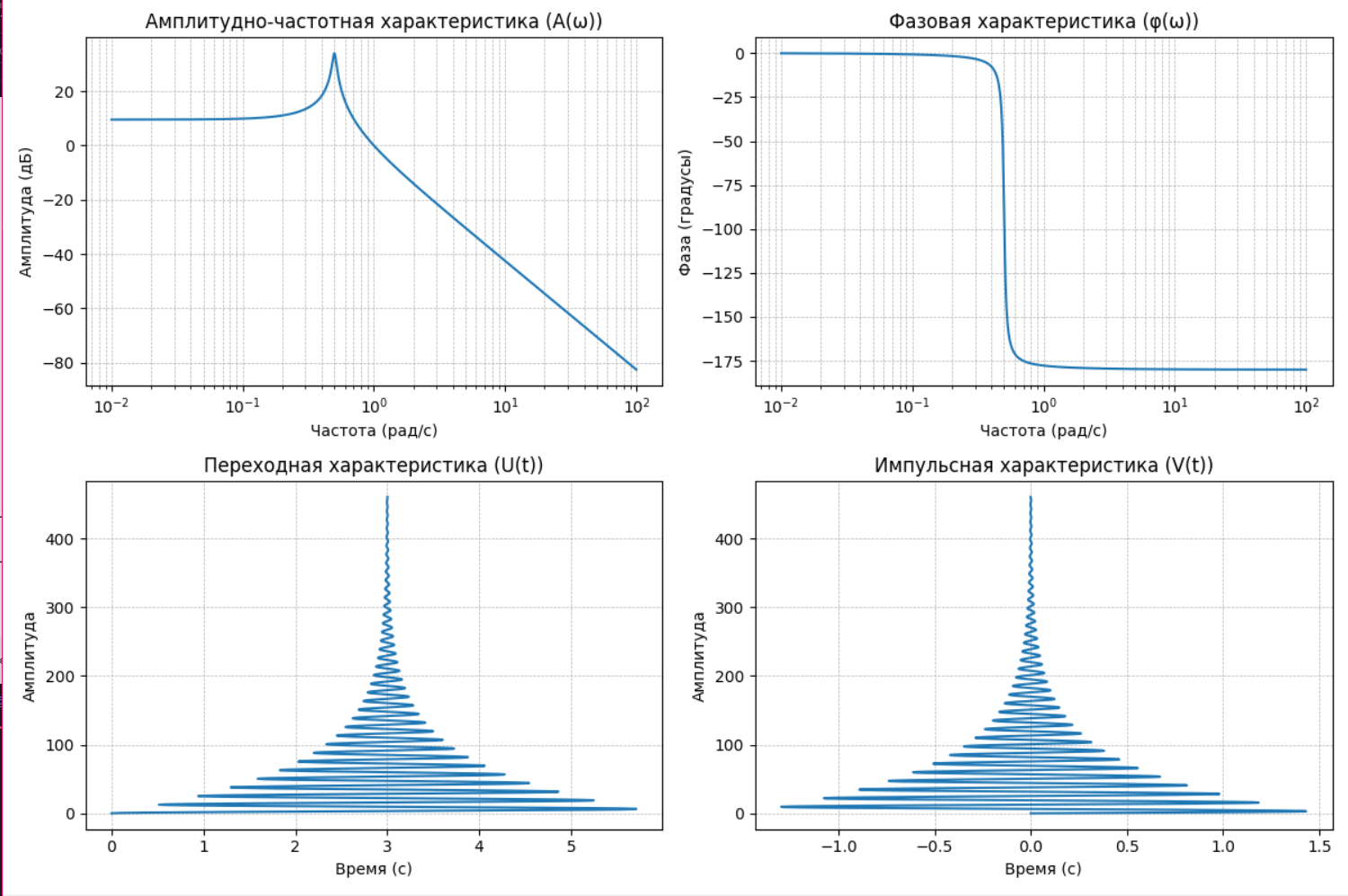
Графики колебательного звена
Амплитудно-частотная характеристика
Этот график (в верхнем левом углу) показывает, как амплитуда выходного сигнала изменяется в зависимости от частоты входного сигнала.
На низких частотах амплитуда остается примерно постоянной, но по мере увеличения частоты наблюдается выраженный пик, связанный с резонансом колебательного звена. Этот пик говорит о том, что на определенной частоте система усиливает сигнал.
После резонансной частоты амплитуда начинает спадать, демонстрируя типичное поведение колебательного звена с затуханием на высоких частотах.
Фазовая характеристика
Этот график (в верхнем правом углу) показывает, как фазовый сдвиг изменяется в зависимости от частоты.
На низких частотах фазовый сдвиг близок к нулю, что означает, что система практически не задерживает сигнал по фазе.
Вблизи резонансной частоты фазовый сдвиг резко меняется, приближаясь к -180 градусам. Это резкое изменение фазы характерно для колебательных систем, в которых на резонансной частоте происходит значительная задержка фазы.
Переходная характеристика
Этот график (в нижнем левом углу) показывает отклик системы на единичный скачок (ступенчатый сигнал) во времени.
В начале система демонстрирует колебательный отклик, амплитуда которого сначала возрастает, достигая максимума, а затем начинает постепенно затухать.
Колебания затухают медленно из-за малого коэффициента затухания ξ\xiξ, что позволяет системе сохранять колебания на протяжении длительного времени.
Импульсная характеристика
Этот график (в нижнем правом углу) показывает отклик системы на единичный импульс.
Подобно переходной характеристике, система демонстрирует колебательный отклик, достигая максимума и затем постепенно затухая.
Импульсная характеристика указывает на то, как система реагирует на мгновенное воздействие, показывая периодические колебания с постепенным спадом амплитуды.
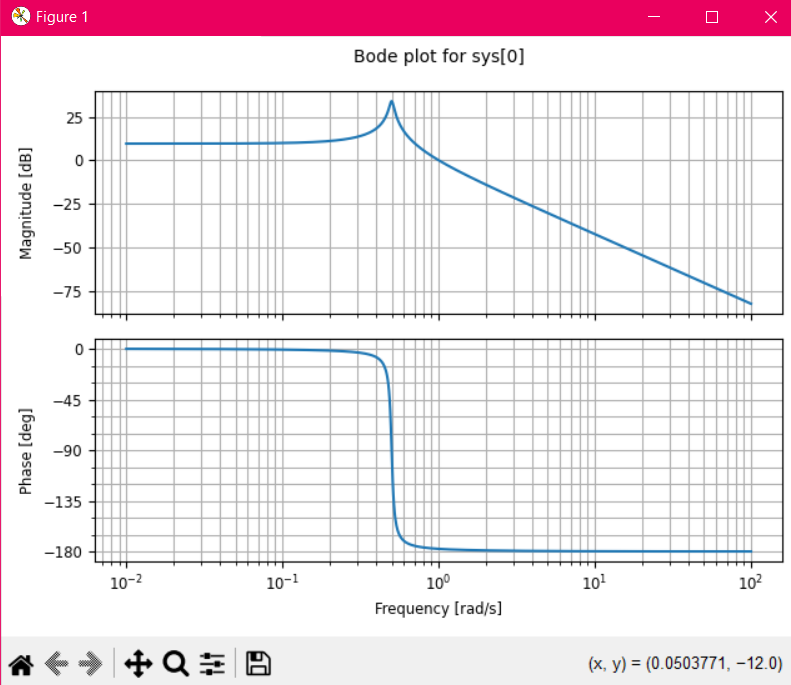
Верхний график — Амплитудно-частотная характеристика (АЧХ):
На этом графике показана зависимость амплитуды выходного сигнала от частоты входного сигнала, измеренная в децибелах (дБ).
На низких частотах амплитуда остается относительно постоянной, что указывает на то, что система пропускает низкочастотные сигналы без значительного усиления или ослабления.
В средней области частот наблюдается выраженный пик — это резонансная частота колебательного звена, где амплитуда достигает максимума. На этой частоте система усиливает сигнал, что характерно для колебательных систем с низким коэффициентом затухания.
После резонансной частоты амплитуда начинает резко падать, демонстрируя поведение фильтра, который ослабляет высокочастотные компоненты сигнала. Падение происходит с уклоном, характерным для колебательных систем.
Нижний график — Фазовая характеристика (ФЧХ):
На этом графике показан фазовый сдвиг сигнала в зависимости от частоты, измеренный в градусах.
На низких частотах фазовый сдвиг близок к 0 градусам, что означает, что система практически не задерживает фазу сигнала при низкочастотных воздействиях.
При приближении к резонансной частоте фазовый сдвиг резко изменяется, переходя к -180 градусам. Это поведение указывает на то, что колебательная система сильно задерживает фазу сигнала на резонансной частоте и выше.
После резонансной частоты фаза стабилизируется около -180 градусов, что указывает на полное запаздывание по фазе для высокочастотных сигналов.

Точная ЛАЧХ (пунктирная линия):
Отображает реальную амплитудную характеристику колебательного звена на логарифмической шкале частоты.
На низких частотах амплитуда остается почти постоянной, что указывает на пропускание низкочастотных сигналов.
На средней частоте виден резонансный пик, где амплитуда резко возрастает. Это связано с тем, что на определенной частоте (резонансной частоте) колебательное звено усиливает сигнал.
После резонансной частоты амплитуда начинает спадать с увеличением частоты, и система ослабляет высокочастотные компоненты сигнала. Это поведение типично для колебательных звеньев, которые после резонансной частоты действуют как фильтры для высоких частот.
Асимптотическая ЛАЧХ (оранжевая линия):
Асимптотическая ЛАЧХ представляет собой упрощенное приближение, которое показывает основные особенности частотного отклика системы.
На низких частотах асимптотическая ЛАЧХ остается на постоянном уровне, что соответствует коэффициенту усиления kkk при низких частотах.
С увеличением частоты асимптотическая ЛАЧХ имеет прямолинейный спад (с наклоном примерно −20-20−20 дБ на декаду), что указывает на ослабление сигнала на высоких частотах. Однако она не показывает резонансного пика, так как не учитывает переходные эффекты системы.
1) Изучить влияние параметров Т и на вид () и L(). Сделать выводы.
Параметр T влияет на положение резонансной частоты, в то время как ξ определяет форму отклика на этой частоте. Меньший ξ делает систему более резонансной, а больший ξ сглаживает колебания, приближая систему к апериодической.
2) Построить в одном окне асимптотическую и точную ЛАЧХ колебательного звена. Сделать выводы.
Асимптотическая ЛАЧХ упрощает анализ системы, но не отображает резонансные эффекты. Точная ЛАЧХ более точно описывает поведение системы, особенно в области резонансной частоты, что важно для оценки реакций колебательных систем.
Код
import numpy as np import matplotlib.pyplot as plt from control.matlab import tf, step, impulse, bode from tkinter import Tk, Label, Entry, Button def build_oscillatory_transfer_function(k, T, xi): # Создание передаточной функции для колебательного звена return tf([k], [T**2, 2*xi*T, 1]) def plot_characteristics(k, T, xi): # Создаем передаточную функцию sys = build_oscillatory_transfer_function(k, T, xi) # Частотный диапазон для построения АЧХ и ФЧХ w = np.logspace(-2, 2, 1000) # Вычисление амплитудно-частотной и фазовой характеристик mag, phase, omega = bode(sys, w) # Построение графиков fig, axs = plt.subplots(2, 2, figsize=(12, 8)) # Амплитудная характеристика (A(ω)) axs[0, 0].semilogx(omega, 20 * np.log10(mag)) axs[0, 0].set_title("Амплитудно-частотная характеристика (A(ω))") axs[0, 0].set_xlabel("Частота (рад/с)") axs[0, 0].set_ylabel("Амплитуда (дБ)") axs[0, 0].grid(True, which="both", linestyle="--", linewidth=0.5) # Фазовая характеристика (φ(ω)) axs[0, 1].semilogx(omega, np.degrees(phase)) axs[0, 1].set_title("Фазовая характеристика (φ(ω))") axs[0, 1].set_xlabel("Частота (рад/с)") axs[0, 1].set_ylabel("Фаза (градусы)") axs[0, 1].grid(True, which="both", linestyle="--", linewidth=0.5) # Переходная характеристика (U(t)) t, y = step(sys) axs[1, 0].plot(t, y) axs[1, 0].set_title("Переходная характеристика (U(t))") axs[1, 0].set_xlabel("Время (с)") axs[1, 0].set_ylabel("Амплитуда") axs[1, 0].grid(True, linestyle="--", linewidth=0.5) # Импульсная характеристика (V(t)) t, y = impulse(sys) axs[1, 1].plot(t, y) axs[1, 1].set_title("Импульсная характеристика (V(t))") axs[1, 1].set_xlabel("Время (с)") axs[1, 1].set_ylabel("Амплитуда") axs[1, 1].grid(True, linestyle="--", linewidth=0.5) plt.tight_layout() plt.show() # Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) - Точная и Асимптотическая plt.figure(figsize=(8, 6)) # Точная ЛАЧХ plt.semilogx(omega, 20 * np.log10(mag), label="Точная ЛАЧХ", linestyle='--') # Асимптотическая ЛАЧХ asymptotic_mag = 20 * np.log10(k) - 20 * np.log10(omega * T) plt.semilogx(omega, asymptotic_mag, label="Асимптотическая ЛАЧХ", linestyle='-') plt.title("Логарифмическая амплитудно-частотная характеристика (L(ω))") plt.xlabel("Частота (рад/с)") plt.ylabel("Амплитуда (дБ)") plt.legend() plt.grid(True, which="both", linestyle="--", linewidth=0.5) plt.show() def start_plotting(): # Получение значений параметров из полей ввода k = float(entry_k.get()) T = float(entry_T.get()) xi = float(entry_xi.get()) plot_characteristics(k, T, xi) # Создание окна интерфейса root = Tk() root.title("Построение характеристик колебательного звена") Label(root, text="Введите значение k:").grid(row=0, column=0) entry_k = Entry(root) entry_k.grid(row=0, column=1) entry_k.insert(0, "3") # Предустановленное значение k Label(root, text="Введите значение T:").grid(row=1, column=0) entry_T = Entry(root) entry_T.grid(row=1, column=1) entry_T.insert(0, "2") # Предустановленное значение T Label(root, text="Введите значение ξ:").grid(row=2, column=0) entry_xi = Entry(root) entry_xi.grid(row=2, column=1) entry_xi.insert(0, "0.03") # Предустановленное значение ξ # Кнопка для построения графиков Button(root, text="Построить графики", command=start_plotting).grid(row=3, column=0, columnspan=2) root.mainloop()

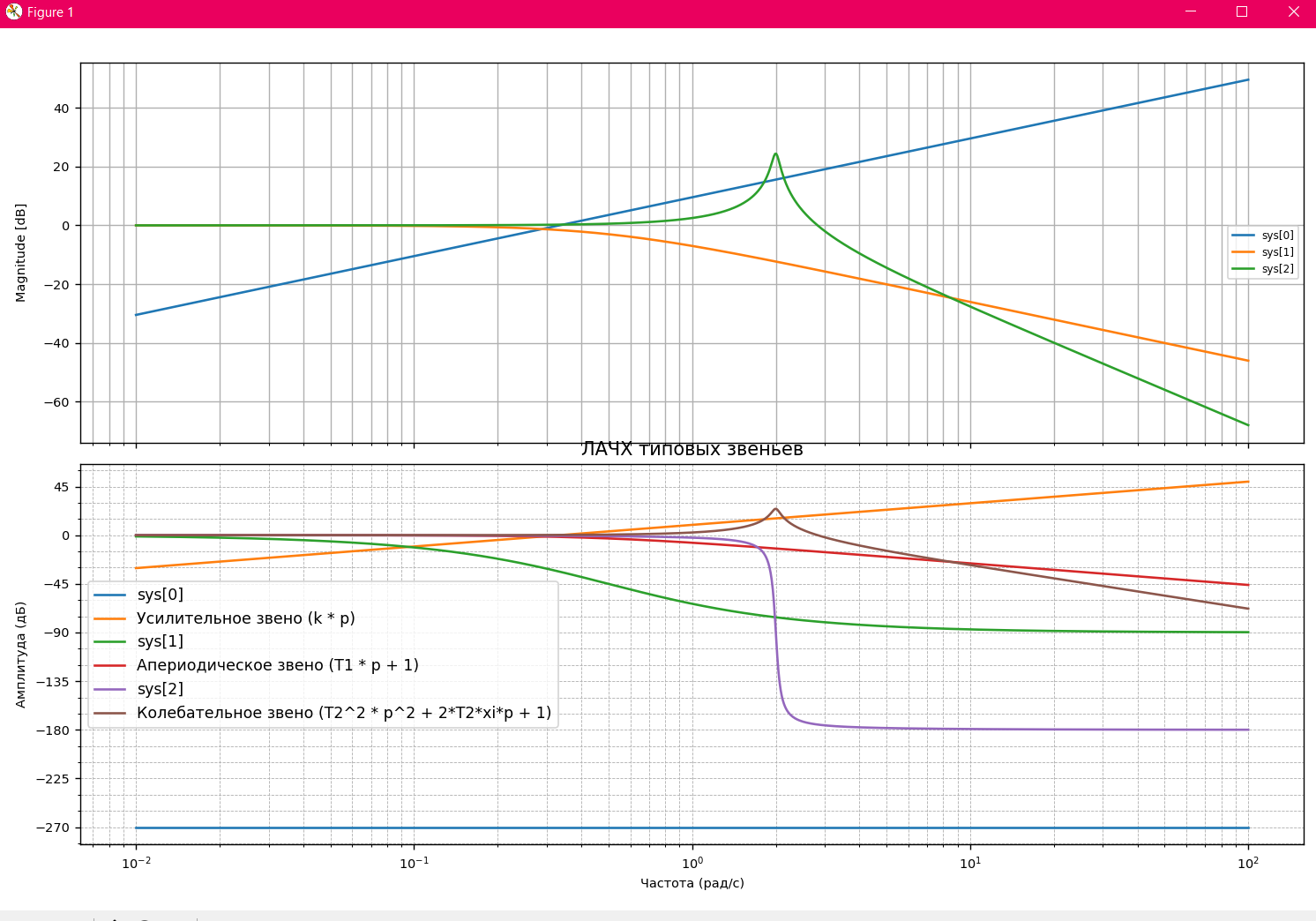
Верхний график — ЛАЧХ типовых звеньев:
Здесь показаны амплитудно-частотные характеристики (АЧХ) отдельных типовых звеньев, входящих в систему.
Видно, что каждое звено имеет свой характерный отклик на частотные изменения:
Усилительное звено (линия, линейно возрастающая с частотой): усиливает сигнал пропорционально частоте.
Апериодическое звено первого порядка (умеренно убывающая линия): ослабляет высокочастотные сигналы, уменьшая амплитуду на высоких частотах.
Колебательное звено второго порядка (линия с резонансным пиком): усиливает сигнал на определенной (резонансной) частоте, после чего амплитуда начинает спадать.
Нижний график — ЛАЧХ для всех типовых звеньев и полной системы:
Этот график включает ЛАЧХ всей системы, а также типовых звеньев. Судя по обозначениям, вы добавили разные линии для каждого из звеньев и всей системы.
Полная система (синяя линия): показывает суммарный отклик всей системы на частотные изменения, с учетом всех типовых звеньев.
На графике видно резонансный пик, характерный для колебательного звена, а также тенденции, соответствующие усилительному и апериодическому звеньям.
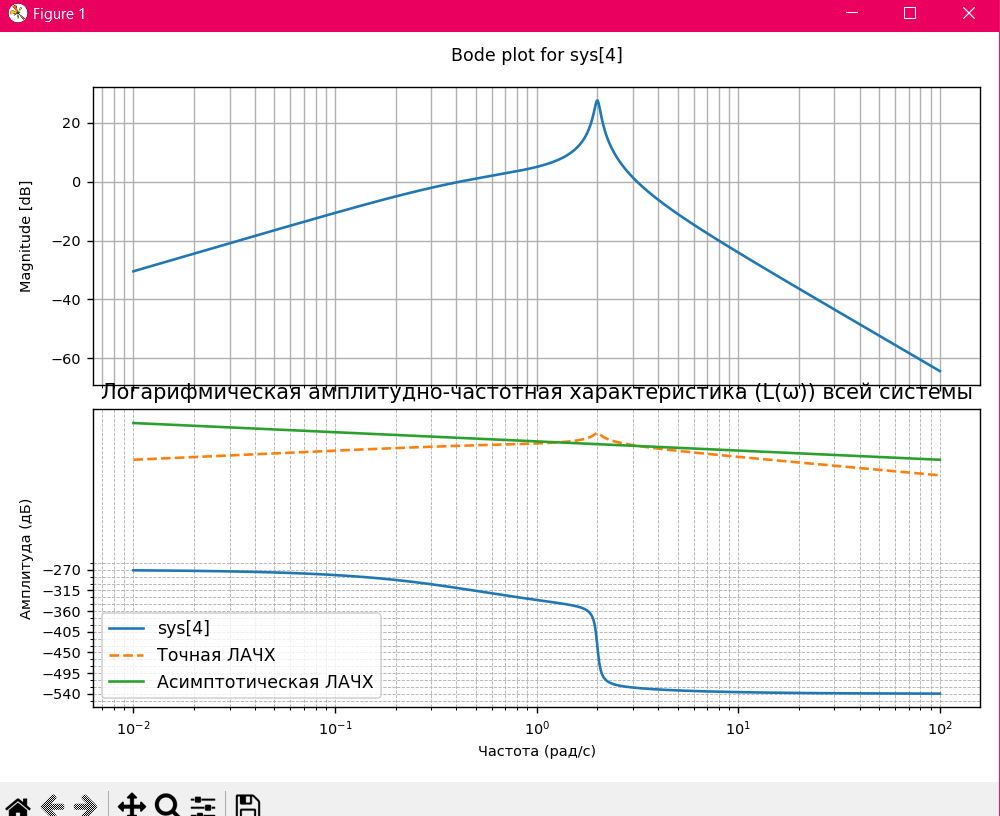
Верхний график — Bode plot (амплитудно-частотная характеристика):
Этот график демонстрирует амплитудный отклик системы (модуль передаточной функции в децибелах) в зависимости от частоты.
Видно, что система имеет резонансный пик, характерный для колебательных систем. На низких частотах амплитуда постепенно увеличивается, затем достигает пика, а после этого начинается спад на высоких частотах.
Нижний график — Точная и асимптотическая ЛАЧХ:
Этот график представляет точную и асимптотическую ЛАЧХ для всей системы.
Точная ЛАЧХ (пунктирная оранжевая линия) показывает более подробное поведение системы, включая резонансный пик.
Асимптотическая ЛАЧХ (сплошная зеленая линия) сглаживает этот пик и упрощает отображение, показывая общую тенденцию снижения амплитуды на высоких частотах.
На низких и высоких частотах обе характеристики (точная и асимптотическая) примерно совпадают, что соответствует ожиданиям.

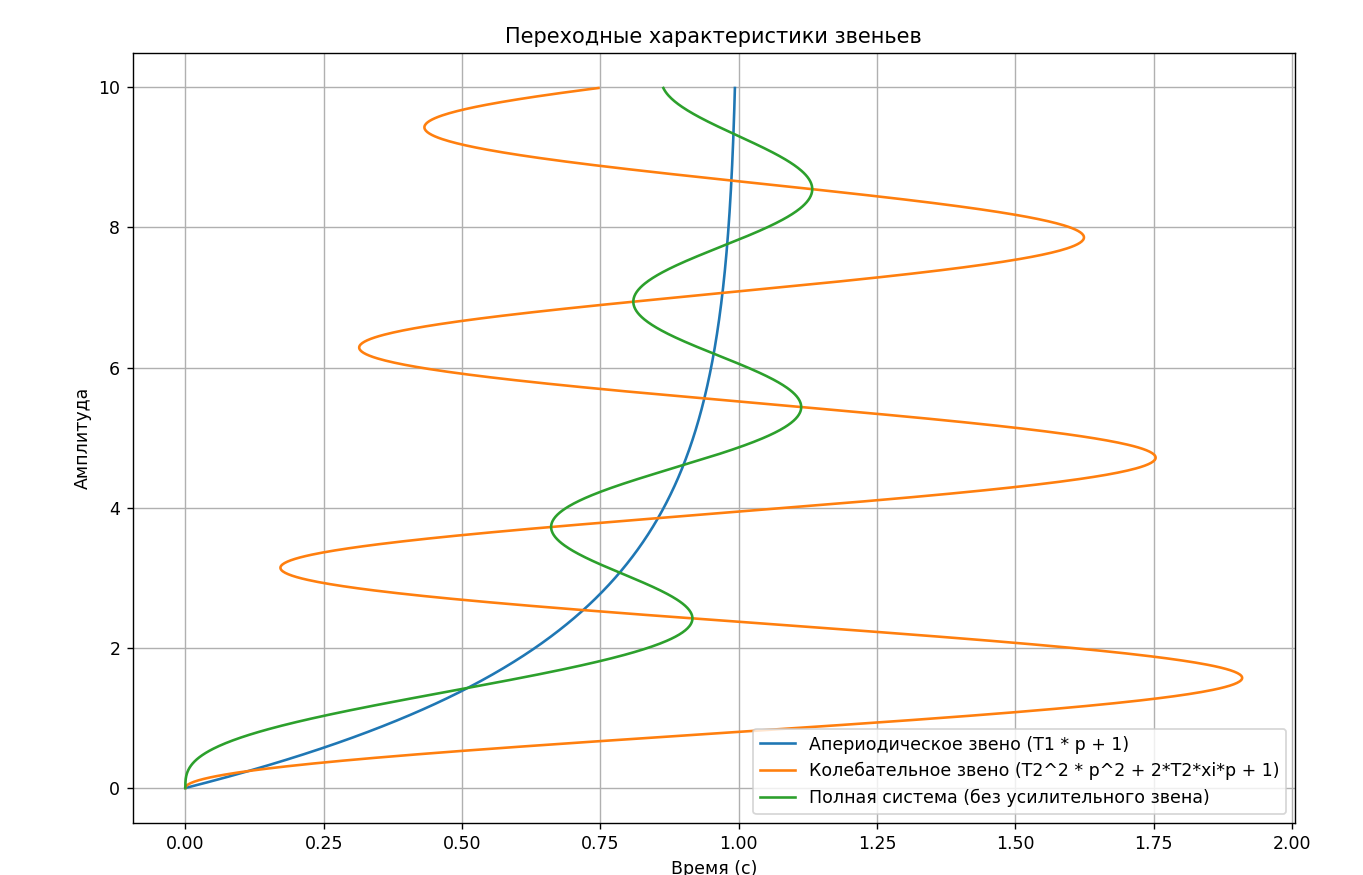
1) построить переходные функции всех упомянутых выше звеньев. По полученным графикам сделать выводы.
Апериодическое звено (синяя линия):
Апериодическое звено первого порядка должно демонстрировать экспоненциальный рост, выходя на постоянное значение. На графике оно действительно показывает такую форму, что соответствует ожидаемому поведению.
Колебательное звено (зеленая линия):
Колебательное звено второго порядка должно демонстрировать затухающие колебания. На графике зеленая линия показывает колебательный отклик, который затухает по мере увеличения времени. Это также соответствует теоретическим ожиданиям.
Полная система (без усилительного звена) (оранжевая линия):
Полная система, состоящая из апериодического и колебательного звеньев, должна демонстрировать комбинацию их свойств, с некоторым колебательным откликом и постепенным выходом на постоянное значение. Оранжевая линия действительно показывает такую форму, что подтверждает корректное поведение.
import numpy as np import matplotlib.pyplot as plt from control.matlab import tf, step, series # Заданные параметры k = 3 T1 = 2 T2 = 0.5 xi = 0.03 # Определение типовых звеньев # Апериодическое звено первого порядка (T1 * p + 1) first_order = tf([1], [T1, 1]) # Колебательное звено второго порядка (T2^2 * p^2 + 2 * T2 * xi * p + 1) second_order_oscillatory = tf([1], [T2**2, 2*T2*xi, 1]) # Полная передаточная функция системы (исключая усилительное звено) system = series(first_order, second_order_oscillatory) # Временной диапазон для переходных характеристик t = np.arange(0, 10, 0.01) # равномерный интервал времени с шагом 0.01 # Построение переходных характеристик plt.figure(figsize=(12, 8)) # Переходная характеристика для апериодического звена первого порядка t1, y1 = step(first_order, T=t) plt.plot(t1, y1, label="Апериодическое звено (T1 * p + 1)") # Переходная характеристика для колебательного звена второго порядка t2, y2 = step(second_order_oscillatory, T=t) plt.plot(t2, y2, label="Колебательное звено (T2^2 * p^2 + 2*T2*xi*p + 1)") # Переходная характеристика для полной системы (без усилительного звена) t3, y3 = step(system, T=t) plt.plot(t3, y3, label="Полная система (без усилительного звена)") plt.title("Переходные характеристики звеньев") plt.xlabel("Время (с)") plt.ylabel("Амплитуда") plt.legend() plt.grid(True) plt.show()
