Z9411_Чурилов_ММ_ЛР3

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КАФЕДРА № 41

ЛАБОРАТОРНАЯ РАБОТА

ЗАЩИЩЕНА С ОЦЕНКОЙ

РУКОВОДИТЕЛЬ

доц., канд. техн. наук, доц.				О. О. Жаринов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЁТ О ЛАБОРАТОРНОЙ РАБОТЕ №3

Изучение методов фильтрации аудиосигналов в MATLAB. Применение рекурсивных фильтров.

по курсу: Мультимедиа технологии

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	Z9411				А. С. Чурилов
			подпись, дата		инициалы, фамилия

Санкт-Петербург

2024

Цель работы

Получить навыки обработки аудиосигналов на примере методов фильтрации сигналов во временной области с использованием рекурсивных цифровых фильтров.

Краткие теоретические сведения

РЦФ (IIR-фильтры) являются эффективным инструментом цифровой обработки сигналов. В отличие от нерекурсивных фильтров с конечной импульсной характеристикой (КИХ, FIR), РЦФ имеют бесконечную импульсную характеристику за счет обратных связей [1].

РЦФ описываются разностным уравнением:

y[n] = a₁y[n-1] + ... + aᵣy[n-R] + b₀x[n] + b₁x[n-1] + ... + bᵣx[n-R],

где x[n] - входной сигнал, y[n] - выходной сигнал, R - порядок фильтра, {aᵢ} и {bᵢ} - коэффициенты фильтра.

РЦФ могут иметь лучшие характеристики по сравнению с КИХ-фильтрами того же порядка - более крутые склоны АЧХ, меньшие искажения фазы. Но они потенциально неустойчивы и чувствительны к эффектам квантования коэффициентов.

Расчет коэффициентов РЦФ по заданным требованиям производится на основе аналоговых фильтров-прототипов (Баттерворта, Чебышева и др.) c применением билинейного преобразования.

Вариант задания с ЛР2:

Вариант №19.

Подавить уровень сигнала в диапазоне 45…55 Гц в 100 раз.

Для большей наглядности изменил диапазон на 45…450 Гц.

Ход работы:

Напишем, программу, которая реализует метод фильтрации на основе рекурсивного цифрового фильтра и выполним ту же последовательность действий, что и в предыдущей лабораторной работе (листинг 1).

Листинг 1 –Метод фильтрации на основе рекурсивного цифрового фильтра

clc, clear, close all % Очистка памяти [input_signal,Fd] = audioread('lr2_output.wav'); N = length(input_signal);% Получить длину данных аудиофайла % Параметры фильтра IIR_Ord=4; % порядок фильтра Rp = 0.5; % неравномерность АЧХ в полосе пропускания, дБ low_freq = 45; % нижняя граничная частота полосы пропускания, Гц up_freq = 450; % верхняя граничная частота полосы пропускания, Гц % Расчет коэффициентов рекурсивного фильтра [b, a] = cheby1(IIR_Ord, Rp, [2*low_freq/Fd 2*up_freq/Fd], 'bandpass'); % Фильтрация сигнала output_signal(:,1) = filter(b, a, input_signal(:,1)); % output_signal(:,2) = filter(b, a, input_signal(:,2)); % Расчет и построение спектров сигналов до и после фильтрации Spectr_input=fft(input_signal(:,1)); Spectr_output=fft(output_signal(:,1)); figure(1) subplot(2,1,1) X=20*log10(abs(Spectr_input)); %Преобразовать в дБ f=[0:(Fd/N):Fd/2]; %Перевести Абсциссу в Гц X=X(1:length(f)); semilogx(f,X); grid; xlabel('Частота, Гц'); ylabel('Уровень, дБ'); title('Амплитудный спектр исходного сигнала') subplot(2,1,2) Y=20*log10(abs(Spectr_output)); %Преобразовать в дБ Y=Y(1:length(f)); semilogx(f,Y); grid; xlabel('Частота, Гц'); ylabel('Уровень, дБ'); title('Амплитудный спектр после фильтрации') % Расчет и построение графика АЧХ фильтра [H, F] = freqz(b,a, N,'whole',Fd); f=0:(Fd/N):Fd/2; A_dB = 20*log10(abs(H(1:length(f)))); figure(2), semilogx(f, A_dB), grid xlabel('Частота, Гц'); ylabel('Коэффициент передачи, дБ'); title('АЧХ рекурсивного фильтра') % Построение графиков сигналов во временной области figure(3) subplot(2,1,1) plot((1:N)/Fd,input_signal(:,1)); xlabel('Время, с'); ylabel('Амплитуда'); title('Исходный сигнал') subplot(2,1,2) plot((1:N)/Fd,output_signal(:,1)); xlabel('Время, с'); ylabel('Амплитуда'); title('Сигнал после фильтрации') % Запись выходного аудиофайла audiowrite('talk_filtered.wav', output_signal, Fd)

График исходного сигнала показан на рисунке 1.

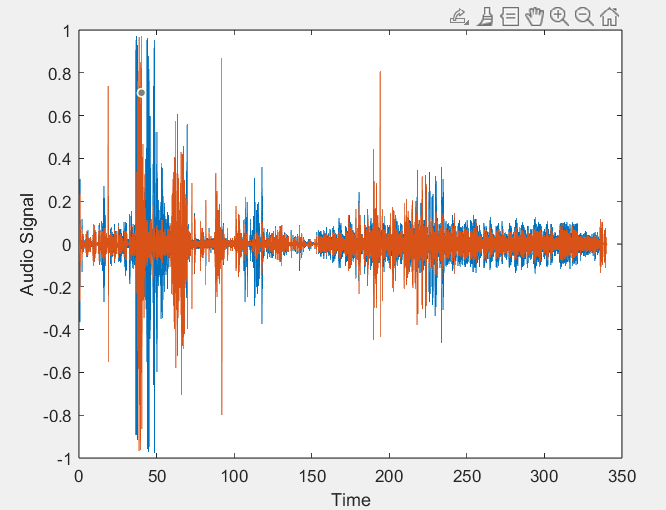
Рисунок 1. График исходного сигнала

Амплитудный спектр исходного сигнала показан на рисунке 2.

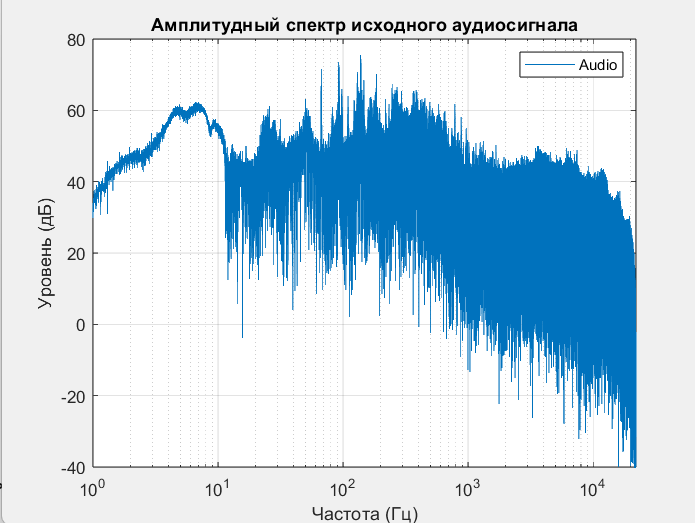
Рисунок 2. Амплитудный спектр исходного сигнала

График изменённого сигнала показан на рисунке 3.

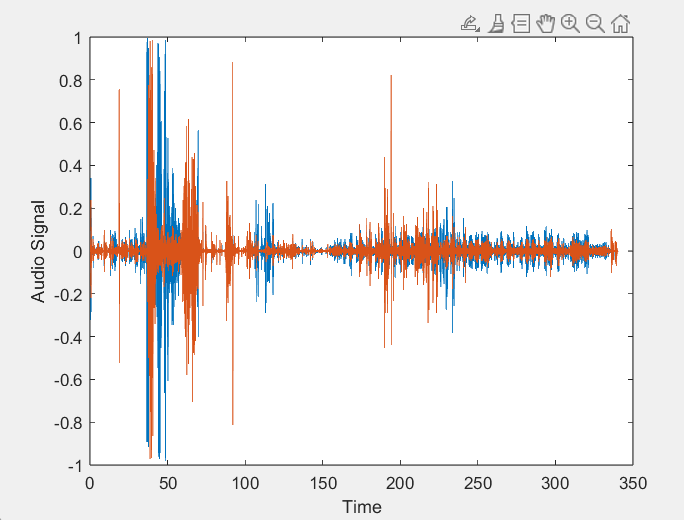
Рисунок 3. График изменённого сигнала

Амплитудный спектр изменённого сигнала показан на рисунке 4.

Рисунок 4. Амплитудный спектр изменённого сигнала

Графики исходного и изменённого сигналов для удобства показаны вместе на рисунке 5.

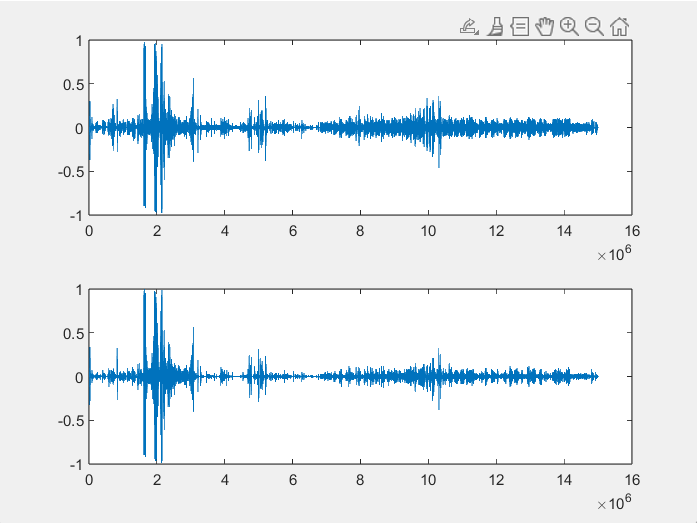
Рисунок 5. Графики сигналов

Как видно из графиков, сигнал действительно изменился. Если прослушать изменённую аудиозапись, то можно услышать, что человеческий голос стал тише и человек как будто говорит «в нос», а вот звук гитары особо не изменился в отличии от исходной аудиозаписи.

ВЫВОД

В данной лабораторной работе я ознакомился с применением рекурсивных цифровых фильтров, которые позволяют эффективно выделять заданные полосы частот в аудиосигнале. По сравнению с Фурье-фильтрацией РЦФ обеспечивают лучшее разделение полос пропускания и подавления при том же порядке фильтра.

Мной была выполнена программа, которая реализует метод фильтрации на основе рекурсивного цифрового фильтра, а также были сравнено звучание аудиозаписей, полученных при выполнении данной и предыдущей лабораторной работы.

Выполнение данной лабораторной работы помогло мне закрепить методы фильтрации аудиосигналов в MATLAB.

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1. Сергиенко А.Б. Цифровая обработка сигналов. 3-е изд. — СПб.: БХВ-Петербург, 2011. — 768 с.

2. Антонью А. Цифровые фильтры: анализ и проектирование. Пер. с англ. — М.: Радио и связь, 1983. — 320 с.

3. Купер Дж., Макгиллем А. Вероятностные методы анализа сигналов и систем: Пер. с англ. — М.: Мир, 1989. — 376 с.