
Z9411_Чурилов_МСРР_ЛР1
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
КАФЕДРА № 41
ЛАБОРАТОРНАЯ РАБОТА
ЗАЩИЩЕНА С ОЦЕНКОЙ
РУКОВОДИТЕЛЬ
старший преподаватель |
|
|
|
И. И. Спиндзак |
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
ОТЧЁТ О ЛАБОРАТОРНОЙ РАБОТЕ №1 |
Механизмы распределения ресурсов нисходящего кадра в телекоммуникационных сетях |
по курсу: Моделирование систем распределения ресурсов |
|
|
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ ГР. № |
Z9411 |
|
|
|
А. С. Чурилов |
|
|
|
подпись, дата |
|
инициалы, фамилия |
Санкт-Петербург
2024
Цель работы:
Получение навыков моделирования стандартных сценариев работы телекоммуникационных систем с топологией типа «звезда». Изучение свойств алгоритмов планирования ресурсов нисходящего кадра в подобных системах.
Вариант задания:
Вариант №19.
№ |
Модель распространения |
R, км |
PTX, Вт |
f0, МГц |
|
kN |
919 |
Окумура-Хата, large city |
3,5 |
160 |
1800 |
5 |
2 |
Расчётные формулы для заданного варианта:
Абсолютную температуру T пример равную 295К, что равняется примерно 21,8С и является допустимой температурой для города.
Рассчитаем мощность шума:
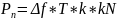
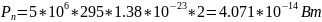
Рассчитаем a(hRX):
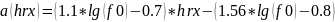
Высоту точки приёма hRX берём равную ср. росту человека – 1.65м
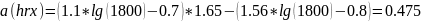
Рассчитаем потери L:
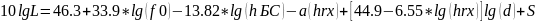
Высоту базовой станции hБС берём равной 40м, S = 3 (большой город)
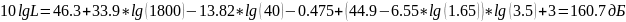
Переведем из «дБ» в «разы»:
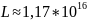
Рассчитаем мощность, принятую АБ:
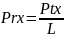
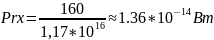
Рассчитаем отношение сигнал/шум:
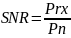
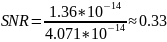
Рассчитаем пропускную способность канала связи:
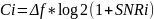
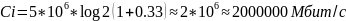
Для проверки был создан программный код, выполняющий эти же расчёты (рисунки 1, 2):
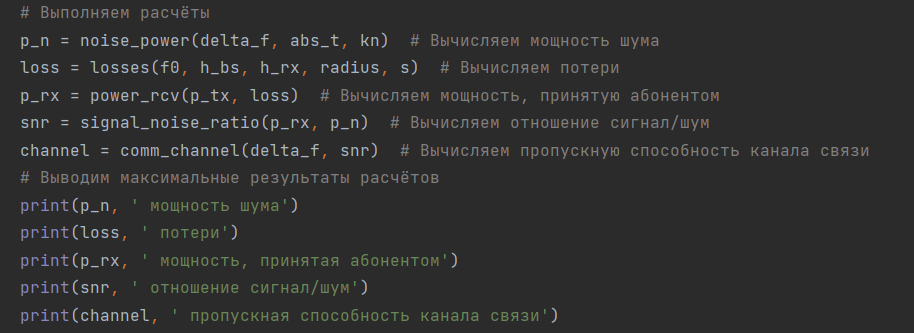
Рисунок 1. Расчёт по заданию
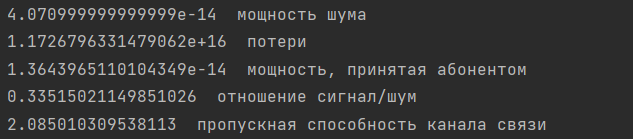
Рисунок 2. Полученные программным путём значения
Значения сходятся с расчётными, поэтому можно сделать вывод, что всё было посчитано правильно.
Полный код программы приведён в Приложении А.
Построение примера расположения абонентов:
Мной было выбрано 8 абонентов, программный код в Приложении А.
Результат выполнения программного кода показан на рисунках 3, 4

Рисунок 3. Максимально достижимые скорости для абонентов
Рисунок 4. График распределения абонентов.
Алгоритмы распределения ресурсов:
Алгоритм Equal Blind
Этот алгоритм дает равные скорости между всеми абонентами.
Доля ресурса времени, выделяемая каждому абоненту, вычисляется по формуле:
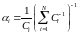
Скорость для абонента i:
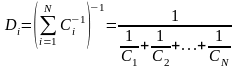
Maximum Throughput:
Это алгоритм применяется для максимизации пропускной способности сети. Формула:
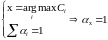
Proportion Fair:
Этот алгоритм выделяет равные ресурсы всем абонентам. Формула:
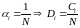
Суммарная скорость:
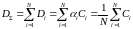
Моделирование алгоритмов распределения ресурсов:
Все построенные далее графики сделаны на основе 100 агрегированных измерений, полученных на основе данных, сгенерированных написанной нами программой.
Построили график зависимости матожидания минимальной скорости передачи от количества абонентов в соответствии с рисунком 5.
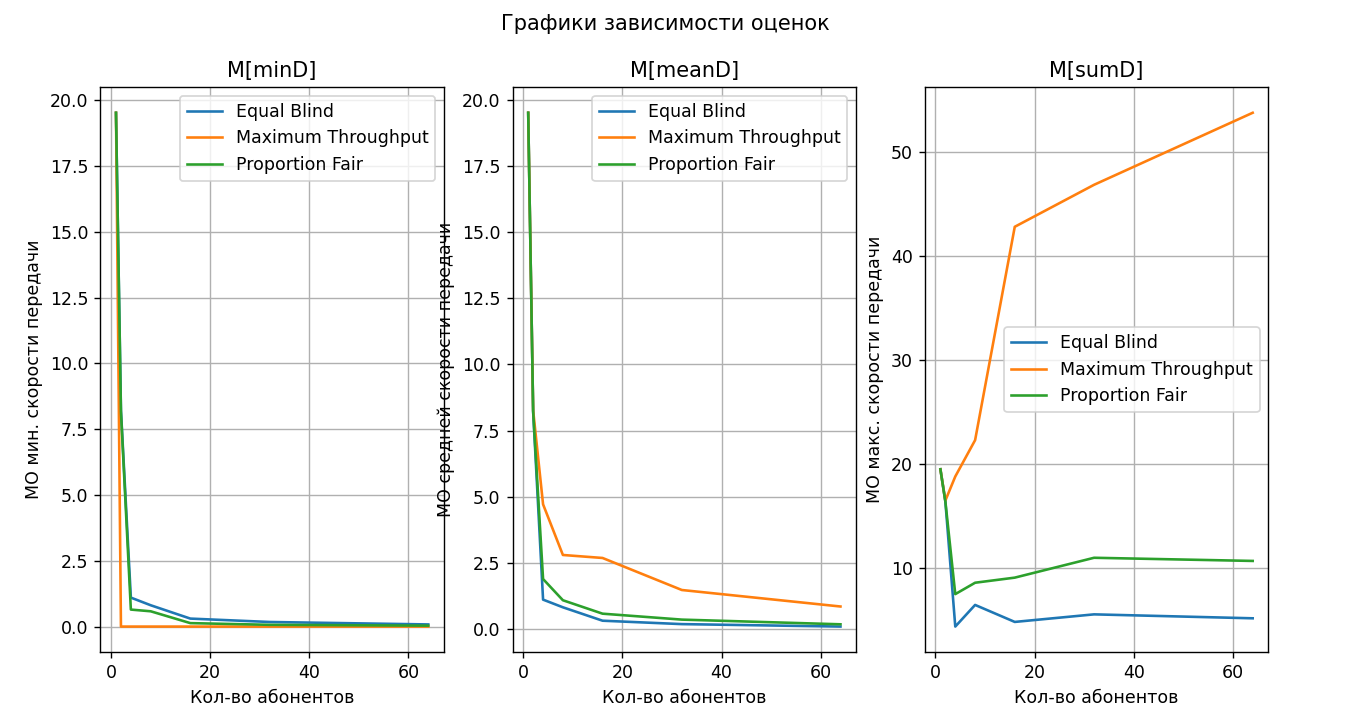
Рисунок 5. Матожидание минимальной скорости передачи в зависимости от количества абонентов
На графики явно выделяется оценка для алгоритма Maximum Throughput. Такой результат связан с тем, что 100% доли ресурса времени, выделяется абоненту с максимальной скоростью передачи, вследствие чего для остальных абонентов скорость равна 0 при количестве абонентов больше 1. Другие два алгоритма показывают примерно одинаковый характер оценки минимальной скорости передачи. Так как алгоритмы Proportion Fair и Equal blind делят ресурсы на всех абонентов, то с ростом их количества абонентов минимальная скорость заметно падает.
Построили график зависимости матожидания средней скорости передачи от количества абонентов в соответствии с рисунком 6.
Рисунок 6. Матожидание средней скорости передачи в зависимости от количества абонентов
Графики для всех алгоритмов схожи, однако алгоритма Maximum Throughput показывает лучшие результаты. Такой результат оценки связан с тем, что с ростом количества абонентов вырастает шанс того, что абонент окажется ближе с базовой станции в следствии чего его скорость передачи заметно вырастет, а так как алгоритм отдает предпочтение абоненту с максимальной скоростью то это значительно влияет на среднюю скорость передачи.
Построили график зависимости матожидания средней скорости передачи от количества абонентов в соответствии с рисунком 7.
Рисунок 7. Матожидание максимальной скорости передачи в зависимости от количества абонентов
На этом графике особенно заметны результаты тех процессов, которые были описаны для алгоритма Maximum Throughput под прошлым графиком, вследствие чего мы получаем заметный рост максимальной скорости передачи с ростом количества абонентов.
Алгоритм Proportion Fair показывает стабильную максимальную скорость передачи, которая практически не изменяется с простом количества абонентов, это связанно с тем, что алгоритм разделяет временной ресурс поровну между всеми абонентами, что в среднем сглаживает оценку скорости передачи.
Алгоритм Equal blind показал самый худший результат так как подбирает равные скорости для всех абонентов, вследствие чего с ростом количества абонентов растет и шанс того, что появятся абоненты с низкой скоростью передачи который понизит общую скорость передачи до своего уровня. Выход на некоторое стабильное плато, когда количество абонентов становится больше 8 свидетельствует о том, что практически каждый раз в зоне действия базовой станции оказывался абонент на максимально возможном удалении с минимальной скоростью передачи.
Данные графиков приведены на рисунке 8.
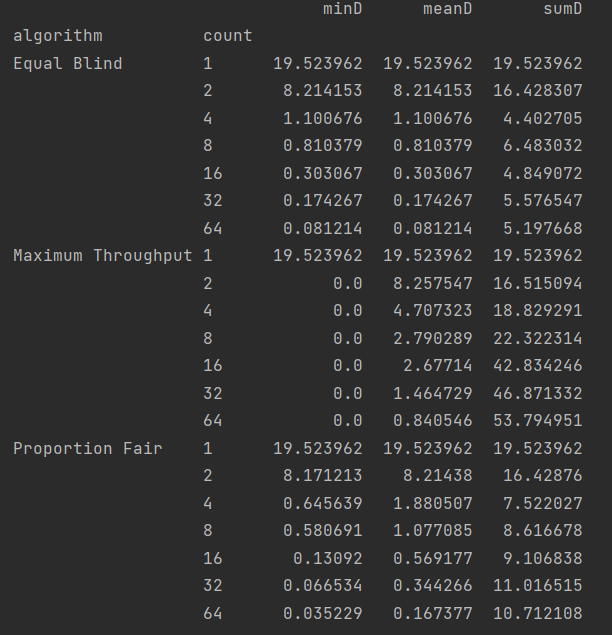
Рисунок 8. Данные графиков зависимостей оценок
Приложение А – Код программы
import numpy as np import pandas as pd from matplotlib import pyplot as plt import math def noise_power(f, t, k): """ Функция расчёта мощности шума :param f: Полоса пропускания канала связи, МгЦ :param t: Абсолютная температура, К :param k: Коэффициент теплового шума приёмника :return: Мощность теплового шума, Вт """ return f * 10 ** 6 * t * 1.38 * 10 ** -23 * k def losses(f0, h_bs, h_rx, d, s): """ Функция расчёта потерь для модели "Окамура-Хаты" :param f0: Частота БС, МгЦ :param h_bs: Высота БС, м :param h_rx: Высота точки приема, м :param d: Расстояние от абонента до башни связи, км :param s: 3 для большого города, 0 для маленького :return: Потери, "разы" """ const1 = math.log10(f0) a_h_rx = (1.1 * const1 - 0.7) * h_rx - (1.56 * const1 - 0.8) loss = 46.3 + 33.9 * const1 - 13.82 * math.log10(h_bs) - a_h_rx + (44.9 - 6.55 * math.log10(h_rx)) * math.log10(d) + s loss = 10 ** (loss / 10) return loss def power_rcv(p_tx, loss): """ Функция расчёта мощности, принятой абонентом :param p_tx: Мощность излучения башни связи, Вт :param loss: Потери, "разы" :return: Мощность, принятая абонентом, Вт """ return p_tx / loss def signal_noise_ratio(p_rx, p_n): """ Функция расчёта отношения сигнал/шум :param p_rx: Мощность, принятая абонентом, Вт :param p_n: Мощность теплового шума, Вт :return: Отношение сигнал/шум """ return p_rx / p_n def comm_channel(delta_f, snr): """ Функция расчёта пропускной способности канала связи :param delta_f: Полоса пропускания канала связи, МгЦ :param snr: Отношение сигнал/шум :return: Пропускная способность канала связи """ return delta_f * math.log2(1 + snr) def graph_location_subs_stations(subs, radius): """Построение графика расположения абонентов""" fig, ax = plt.subplots(subplot_kw={'projection': 'polar'}) ax.scatter(subs['angle'], subs['distance']) ax.set_rmax(radius) if len(subs) == 1: plt.title(f'Распределение {len(subs)} абонента', ) else: plt.title(f'Распределение {len(subs)} абонентов', ) plt.show() return 0 def subs_creation(radius, n, p_n, f0, h_bs, h_rx, s, p_tx, delta_f): """Генерация списка расположения абоненских станций""" subs = pd.DataFrame(columns=['distance', 'angle', 'x', 'y', 'channel']) for i in range(n): distance = np.sqrt(radius ** 2 * np.random.random()) # Дистанция от абонента до башни связи angle = 2 * np.pi * np.random.random() # Угол координат x = distance * np.cos(angle) y = distance * np.sin(angle) loss = losses(f0, h_bs, h_rx, distance, s) # Вычисляем потери p_rx = power_rcv(p_tx, loss) # Вычисляем мощность, принятую абонентом snr = signal_noise_ratio(p_rx, p_n) # Вычисляем отношение сигнал/шум sub_channel = comm_channel(delta_f, snr) # Вычисляем пропускную способность канала связи print(f'Максимально достижимая скорость для абонента №{i + 1}' f' x({x}):y({y}):angle({angle}) - {sub_channel} мбит/сек') subs = pd.concat( [ subs, pd.Series({'distance': distance, 'angle': angle, 'x': x, 'y': y, 'channel': sub_channel} ).to_frame().T ], ignore_index=True) return subs def equal_blind(channel): """Алгоритм ПРС - Равные скорости абонентам""" d = sum([c ** -1 for c in channel]) ** -1 return pd.Series({'algorithm': 'Equal Blind', 'count': len(channel), 'minD': d, 'meanD': d, 'sumD': d * len(channel)}).to_frame().T def maximum_throughput(channel): """Алгоритм ПСС - Максимальная суммарная скорость передачи данных""" equal_max = np.array(channel) == max(channel) d = [1 / sum(equal_max) * v * equal_max[i] for i, v in enumerate(channel)] return pd.Series({'algorithm': 'Maximum Throughput', 'count': len(channel), 'minD': min(d), 'meanD': np.mean(d), 'sumD': sum(d)}).to_frame().T def proportion_fair(channel): """Алгоритм ПРД - Равные доли выделенных ресурсов""" d = [cc / len(channel) for cc in channel] return pd.Series({'algorithm': 'Proportion Fair', 'count': len(channel), 'minD': min(d), 'meanD': np.mean(d), 'sumD': sum(d)}).to_frame().T def plot_grade(grade): """Построение графиков измеренных величин""" fig, axs = plt.subplots(1, 3) fig.suptitle('Графики зависимости оценок') x_axis = 'count' y_axis = ['minD', 'meanD', 'sumD'] x_lable = 'Кол-во абонентов' y_lable = ['МО мин. скорости передачи', 'МО средней скорости передачи', 'МО макс. скорости передачи'] grade = grade.reset_index(level=['algorithm', 'count']) groups = grade.groupby('algorithm') for idx in range(3): for n, g in groups: axs[idx].plot(g[x_axis], g[y_axis[idx]], label=n) axs[idx].set_xlabel(x_lable) axs[idx].set_ylabel(y_lable[idx]) axs[idx].set_title(f'M[{y_axis[idx]}]') axs[idx].legend() axs[idx].grid(True) plt.show() return 0 def get_grade(radius, subs, channel, quantity_measurement, p_n, f0, h_bs, h_rx, s, p_tx, delta_f): """Определение мат ожидания для суммарной скорости передачи""" grade = pd.DataFrame(columns=['algorithm', 'count', 'minD', 'meanD', 'sumD']) for i in subs: subs_created = subs_creation(radius, i, p_n, f0, h_bs, h_rx, s, p_tx, delta_f) graph_location_subs_stations(subs_created, radius) for x in range(quantity_measurement): grade = pd.concat([grade, equal_blind(subs_created['channel'])], ignore_index=True) grade = pd.concat([grade, maximum_throughput(subs_created['channel'])], ignore_index=True) grade = pd.concat([grade, proportion_fair(subs_created['channel'])], ignore_index=True) grade.set_index(['algorithm', 'count'], inplace=True) grade = grade.groupby(level=['algorithm', 'count']).mean() plot_grade(grade) return grade def main(radius, p_tx, f0, delta_f, kn, abs_t, h_bs, h_rx, s, subs, quantity_measurement): """ :param radius: Радиус окружности, км :param p_tx: Мощность излучения башни связи, Вт :param f0: Частота башни связи, МгЦ :param delta_f: Полоса пропускания канала связи, МгЦ :param kn: Коэффициент теплового шума приёмника :param abs_t: Абсолютная температура, К :param h_bs: Высота башни связи, м :param h_rx: Высота точки приема, м :param s: 3 для большого города, 0 для маленького :param subs: количество абонентов в виде списка :param quantity_measurement: количество изменений """ # Выполняем расчёты p_n = noise_power(delta_f, abs_t, kn) # Вычисляем мощность шума loss = losses(f0, h_bs, h_rx, radius, s) # Вычисляем потери p_rx = power_rcv(p_tx, loss) # Вычисляем мощность, принятую абонентом snr = signal_noise_ratio(p_rx, p_n) # Вычисляем отношение сигнал/шум channel = comm_channel(delta_f, snr) # Вычисляем пропускную способность канала связи # Выводим максимальные результаты расчётов print(p_n, ' мощность шума') print(loss, ' потери') print(p_rx, ' мощность, принятая абонентом') print(snr, ' отношение сигнал/шум') print(channel, ' пропускная способность канала связи') grade = get_grade(radius, subs, quantity_measurement, p_n, f0, h_bs, h_rx, s, p_tx, delta_f) print(grade) if __name__ == "__main__": test_radius = 3.5 # Радиус окружности, км test_p_tx = 160 # Мощность излучения БС, Вт test_f0 = 1800 # Частота БС, МгЦ test_delta_f = 5 # Полоса пропускания канала связи, МгЦ test_kn = 2 # Коэффициент теплового шума приёмника test_abs_t = 295 # Абсолютная температура, К test_h_bs = 40 # Высота БС, м test_h_rx = 1.65 # Высота точки приема, м test_s = 3 # 3 для большого города, 0 для маленького test_subs = [1, 2, 4, 8, 16, 32, 64] # Количество абонентов test_quantity_measurement = 100 main(test_radius, test_p_tx, test_f0, test_delta_f, test_kn, test_abs_t, test_h_bs, test_h_rx, test_s, test_subs, test_quantity_measurement)
Выводы:
В ходе данной лабораторной работы мы освоили моделирование стандартных сценариев работы телекоммуникационных систем с топологией типа «звезда» и изучены свойства алгоритмов планирования ресурсов нисходящего кадра в подобных системах.
Также было замечено что алгоритмы, не отдающие приоритет какому-то одному абоненту, показывают очень близкие результаты оцениваемых параметров. К таким алгоритмам можно отнести Equal Blind и Proportion Fair они разделяют ресурсы между всеми абонентами. Но даже среди них можно выделить аутсайдера по максимальной скорости для нашей дальности действия базовой станции в 2 км и количестве абонентов больше 8, им оказался алгоритм Equal Blind из-за того, что он выравнивает скорости между всеми абонентами.
Отдельно стоит отметить алгоритм Maximum Throughput так как он благодаря механике своей работы разительно отличится от двух других с которым мы его сравнивали.
Так как данный алгоритм отдает приоритет абоненту с максимальной скоростью передачи минимальная скорость для него равна 0 при количестве абонентов больше 1, а максимальная скорость заметно растет с ростом количества абонентов, хотя в среднем оказывается не сильно выше остальных.

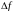 ,
МГц
,
МГц