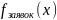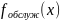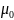МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

КАФЕДРА 41

ОЦЕНКА

ПРЕПОДАВАТЕЛЬ

старший преподаватель				М. Н. Шелест
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ПРАКТИЧЕСКОЙ РАБОТЕ №1

МОДЕЛИРОВАНИЕ ЭЛЕМЕНТАРНОЙ СМО С БЕСКОНЕЧНЫМ БУФЕРОМ

по дисциплине: Имитационное моделирование

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	Z9411				А. С. Чурилов
	номер группы		подпись, дата		инициалы, фамилия
Студенческий билет №	2019/3684

Санкт-Петербург 2024

Цель работы

Нахождение экспериментальной зависимости 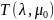для элементарной системы массового обслуживания с бесконечным буфером.

Ход работы

Вариант №18: Порядок эрланговского потока – 2; параметр  – 18.

№ варианта	Закон распределения входного потока заявок	Закон распределения времени обслуживания заявок
8	Экспоненциальный	равномерный	3

Правило поступления потока заявок в систему:

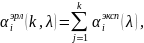
где

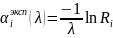
Графики законов распределения вероятностей представлены на рисунках 1-2.

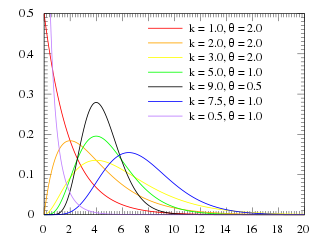Рисунок 1 – Плотность вероятности

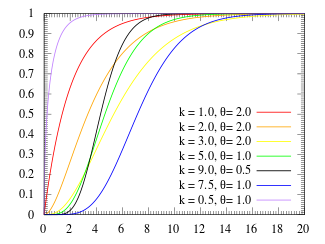Рисунок 2 – Функция распределения

Распределение времени обслуживания заявок: 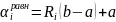, где Ri – случайное число в диапазоне [0,1]

График равномерного распределения вероятностей закона распределения времени обслуживания заявок 𝑓обслуж(𝑥) для времени обслуживания заявок представлен на рисунке 3.

Рисунок 3 – График закона распределения вероятностей для времени обслуживания заявок

Описание разработанной программы

В таблице 1 приведён список переменных для используемых функций в программе.

Таблица 1. Список используемых переменных

Имя переменной	Описание переменной
Функция plot_expon_distribution
lambda_
figure	Атрибут для создания фигуры
Функция plot_uniform_distribution
a	Данные для определения границ
b	Данные для определения границ
figure	Атрибут для создания фигуры
Функция model_of_queuing_system
mu
l	Значение интенсивности входного потока
is_test	Статус тестовый или экспериментальный запуск программы
Функция some_experiments
mu
is_test	Статус тестовый или экспериментальный запуск программы
figure	Атрибут для создания фигуры

Код листинга представлен на рисунках 3-8

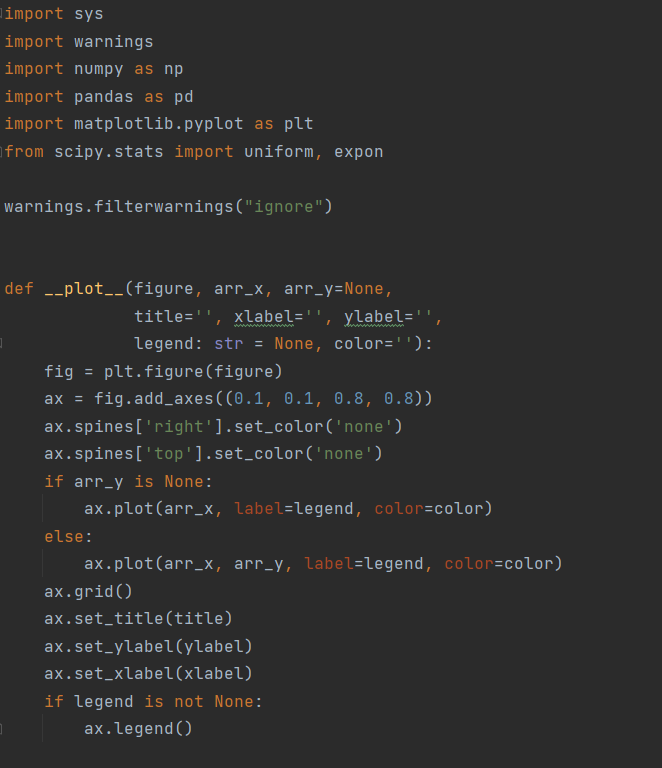
Рисунок 3 – Код программы

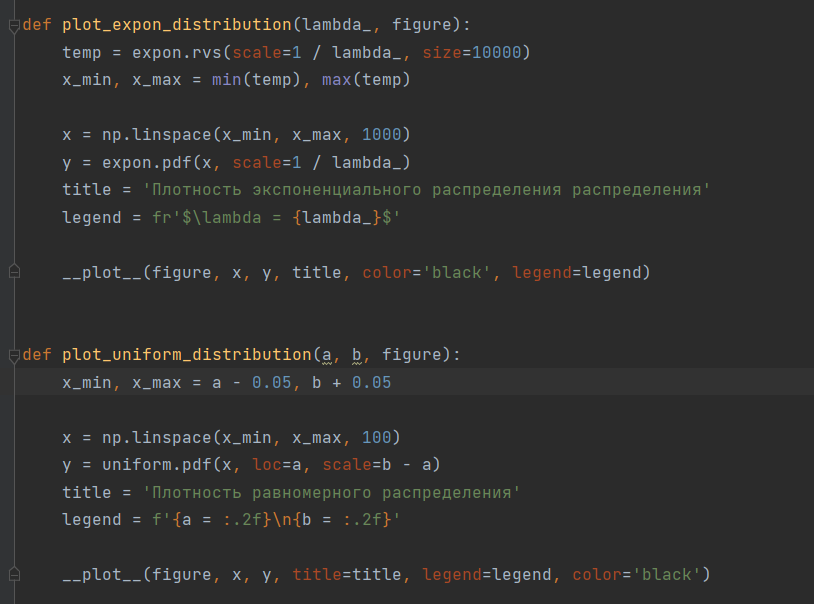
Рисунок 4 – Код программы

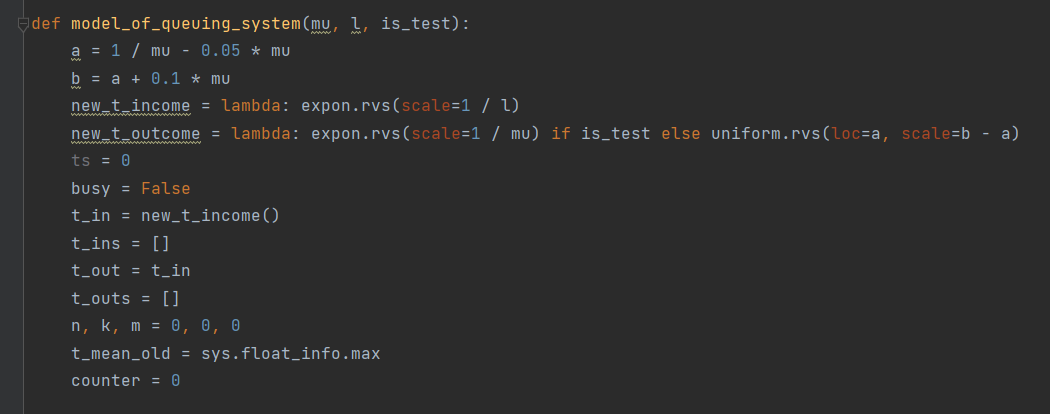
Рисунок 5 – Код программы

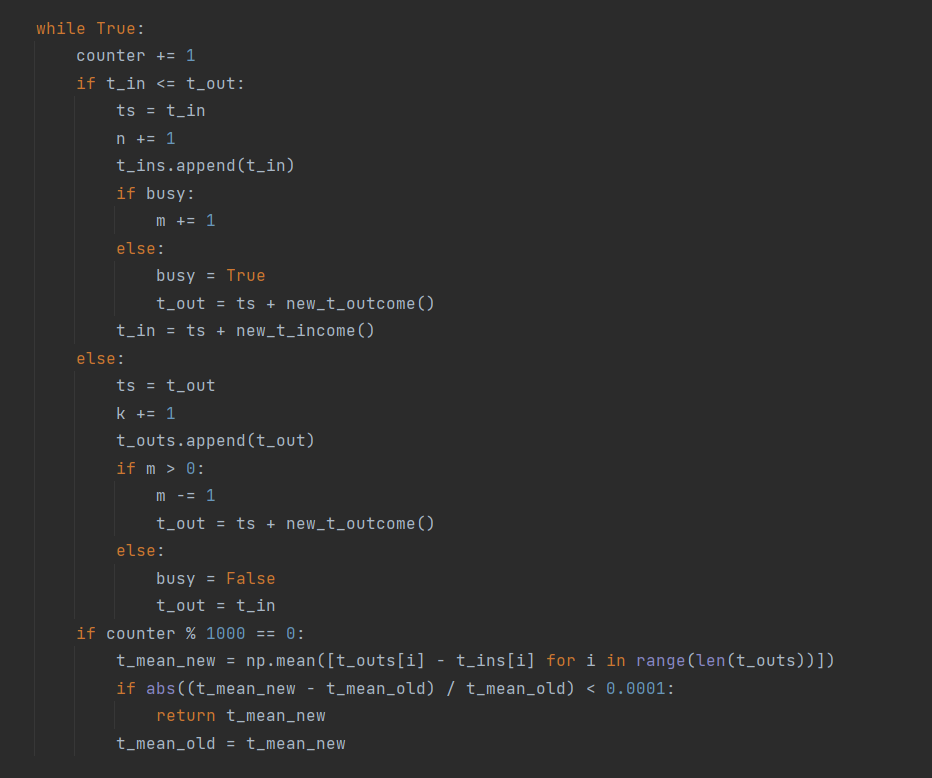
Рисунок 6 – Код программы

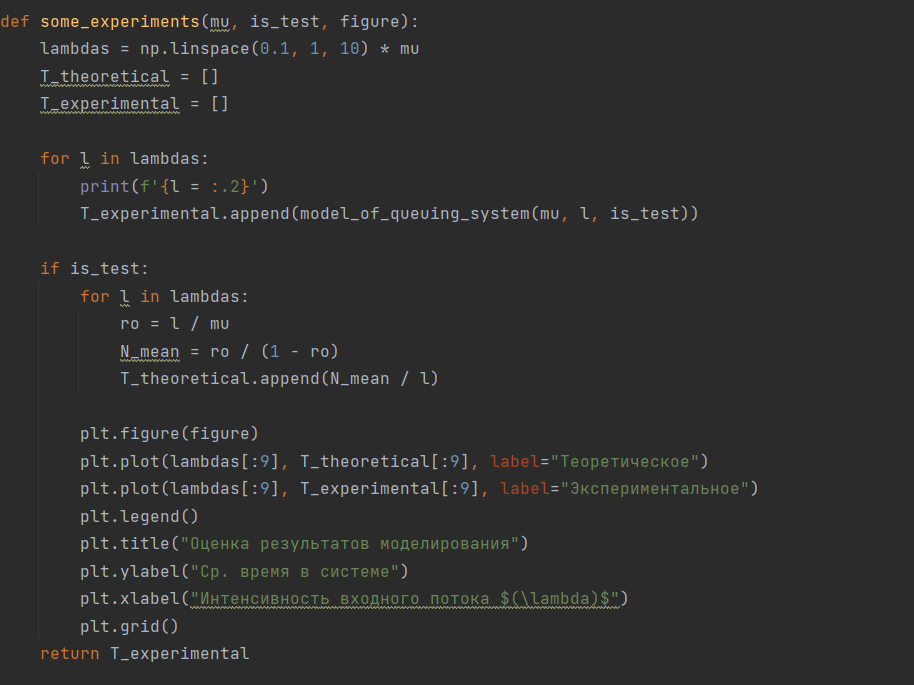
Рисунок 7 – Код программы

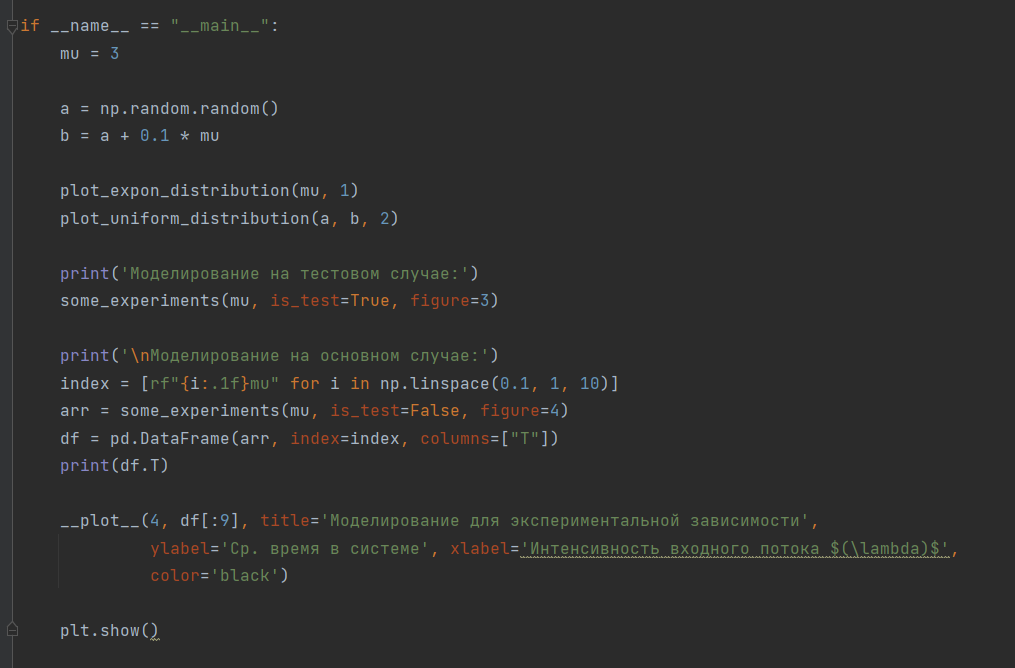
Рисунок 8 – Код программы

Полученные графики показаны на рисунках 9-11.

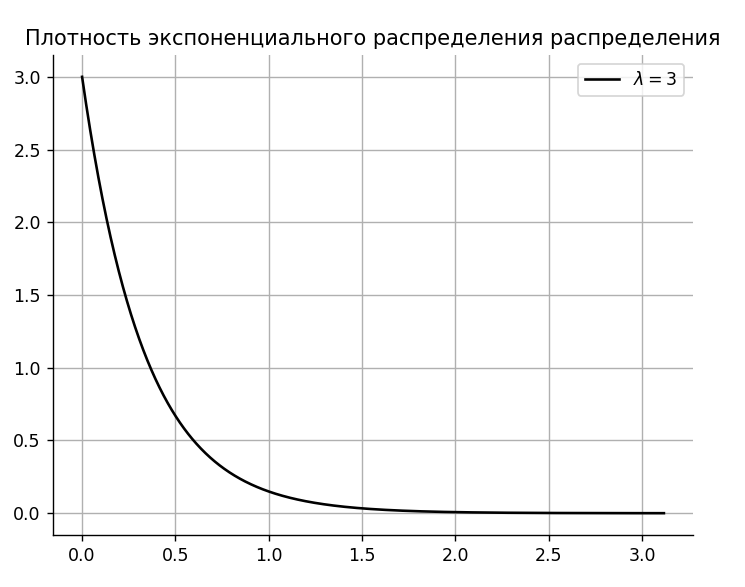
Рисунок 9 – Плотность экспоненциального распределения

Рисунок 10 – Плотность равномерного распределения

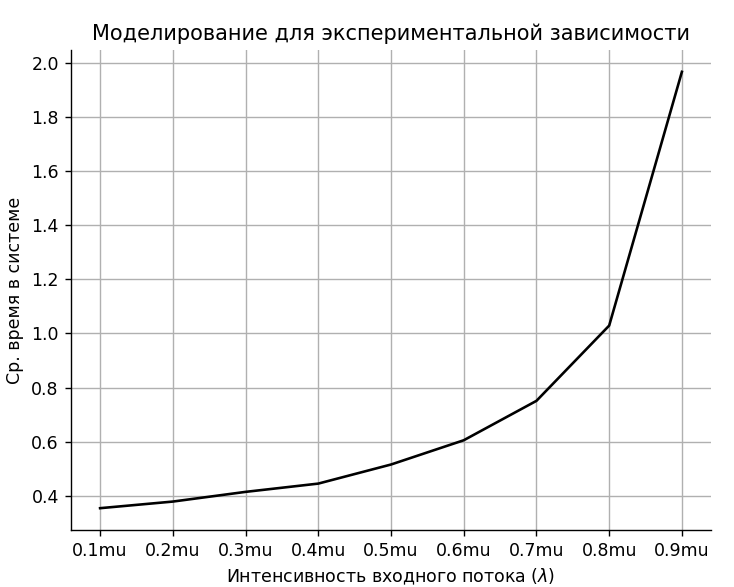
Рисунок 11 – Моделирование для экспериментальной зависимости

График плотности вероятности, построенный по смоделированному экспоненциальному потоку представлен на рисунке 8.

Теоретический и экспериментальный графики зависимости среднего времени пребывания заявки в системе от интенсивности входного потока для тестового примера представлен на рисунке 9.

Провёл моделирование для получения требуемой экспериментальной зависимости. Полученные данные внёс в таблицу 2.

Таблица 2

Параметр	Значение
λ	0.3	0.6	0.9	1.2	1.5	1.8	2.1	2.4	2.7	3
T	0.3	0.4	0.45	0.6	0.75	0.9	1.15	1.7	3.1	4

График зависимости показан на рисунке 12.

Рисунок 12 – График зависимости

Вывод

В ходе моделирования был реализован экспоненциальный равномерный закон распределения 3 порядка для входного потока заявок и равномерный закон распределения времени обслуживания заявок. Разработанная программа моделировала случайное время появления заявок и время их обслуживания. В зависимости от параметров времени и заполненности буфера она принимала решения об обработках заявок, а мы фиксировали время поступления и обслуживания заявок, по которым потом определяли среднее время нахождения заявки в системе. Расчет средних значений позволил нам построить график зависимости среднего времени пребывания запроса от интенсивности входного потока. Расчеты были проведены при разных значениях интенсивности в диапазоне значений λ = 0.1µ0, 0.2µ0, …, 1µ0, поэтому на графике явно видно, что чем больше интенсивность тем больше среднее время обслуживания. Полученный результат согласуется с нашими представлениями об ЭСМО с постоянным входным потоком и временем обслуживания заявок.