
Z9411_Чурилов_ИМ_ЛР
.docxМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
КАФЕДРА 41 |
ОЦЕНКА
ПРЕПОДАВАТЕЛЬ
старший преподаватель |
|
|
|
М. Н. Шелест |
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1
|
МОДЕЛИРОВАНИЕ ВХОДНОГО ПОТОКА ЗАПРОСОВ |
по дисциплине: Имитационное моделирование |
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ гр. № |
Z9411 |
|
|
|
А. С. Чурилов |
|
номер группы |
|
подпись, дата |
|
инициалы, фамилия |
Студенческий билет № |
2019/3684 |
|
|
|
|
Санкт-Петербург 2024
Цель работы
Исследование основных характеристик входных потоков заявок, а также базовых принципов моделирования СМО по событиям.
Ход работы
Вариант №18: Порядок эрланговского потока – 2; параметр – 18.
В начале выполнения данной лабораторной работы необходимо выяснить, как выглядит моделируемый закон распределения. Формула моделируемого закона показана на рисунке 1.

Рисунок 1 – Формула моделируемого закона
Далее, на рисунке 2 показана функция распределения моделируемого закона.
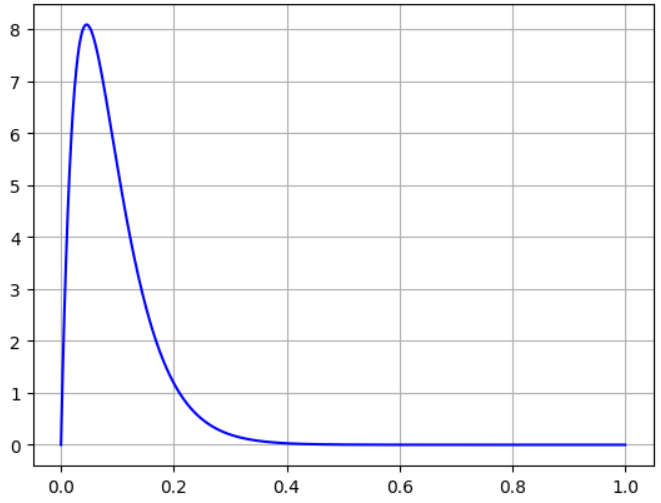
Рисунок 2 – Функция распределения закона
Также, в качестве ознакомительной части определим теоретические значения интенсивности и коэффициента вариации исходного потока.
Оценку интенсивности вычислил по формуле:
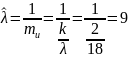
Формула для показателя вариации:
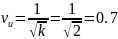
Описание разработанной программы
В таблице 1 приведён список переменных для используемых функций в программе.
Таблица 1. Список используемых переменных
Имя переменной |
Описание переменной |
Функция ploting_erlang_distribution |
|
k |
Порядок эрланговского потока |
lamda |
Параметр потока λ |
data |
Список чисел для построения гистограммы. Если список пуст, генерируются новые данные. |
n |
Количество случайных чисел для генерации, если data пуст |
iner_cnt |
Количество интервалов для гистограммы. |
add_hist |
Флаг, указывающий, следует ли добавить гистограмму на график. |
weights |
Веса столбцов гистограммы. |
intervals, entries, x_min, x_max, delta |
Результаты функции slicearray |
f |
Функция плотности вероятности Эрланговского распределения. |
x |
Список значений x для построения графика. |
Функция random_erlang_val |
|
k |
Параметр формы для Эрланговского распределения. |
lamda |
Параметр масштаба для Эрланговского распределения. |
N |
Количество случайных чисел для генерации. |
f |
Вспомогательная функция для генерации случайного числа, распределенного по закону Эрланга. |
Функция slice_array |
|
array |
Список чисел для разбиения на интервалы. |
intervals_cnt |
Количество интервалов для разбиения списка. |
interval |
Список интервалов. |
entries |
Список количества попаданий в каждый интервал. |
x_min, x_max |
Минимальное и максимальное значения в списке. |
delta |
Длина каждого интервала. |
x, i |
Вспомогательные переменные для циклов. |
Функция ploting_lambda_nu |
|
k |
Порядок эрланговского потока |
lamda |
Параметр потока λ |
lmbda_list, nu_list |
Списки оценок интенсивности и коэффициента вариации. |
n_array |
Список значений объема выборки. |
lambda_t, nu_t |
Теоретические значения интенсивности и коэффициента вариации. |
fig, axis |
Объекты графиков. |
Функция erlang_model |
|
k |
Порядок эрланговского потока |
lamda |
Параметр потока λ |
n |
Начальный объем выборки. |
lmbda_old, nu_old |
Старые оценки интенсивности и коэффициента вариации. |
lmbda_list, nu_list |
Списки для хранения оценок интенсивности и коэффициента вариации. |
u_list |
Список значений выборки Эрланговского распределения. |
loop_cnt |
Счетчик цикла. |
n_array |
Список значений объема выборки. |
me, sigma |
Оценки математического ожидания и дисперсии |
lmbda_new, nu_new |
Новые оценки интенсивности и коэффициента вариации. |
Код листинга представлен на рисунках 3-7
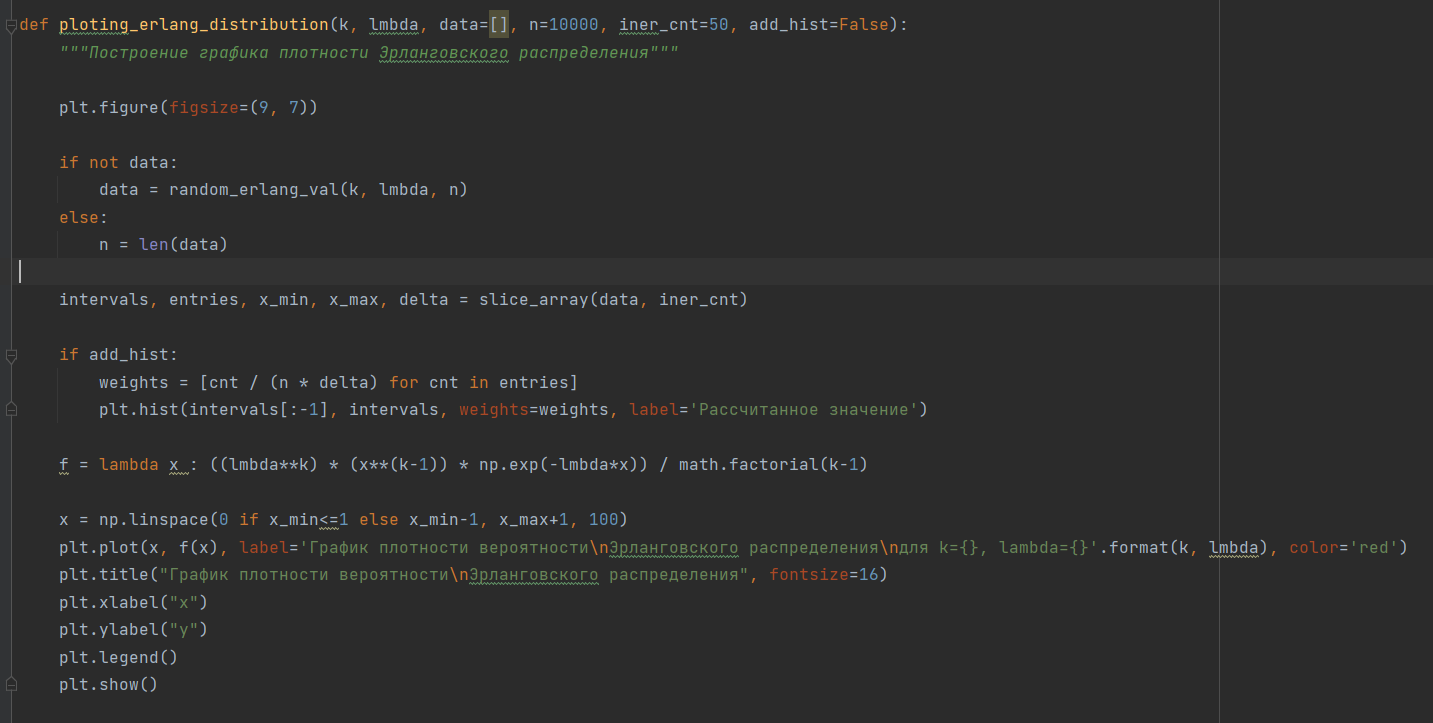
Рисунок 3 – Код программы
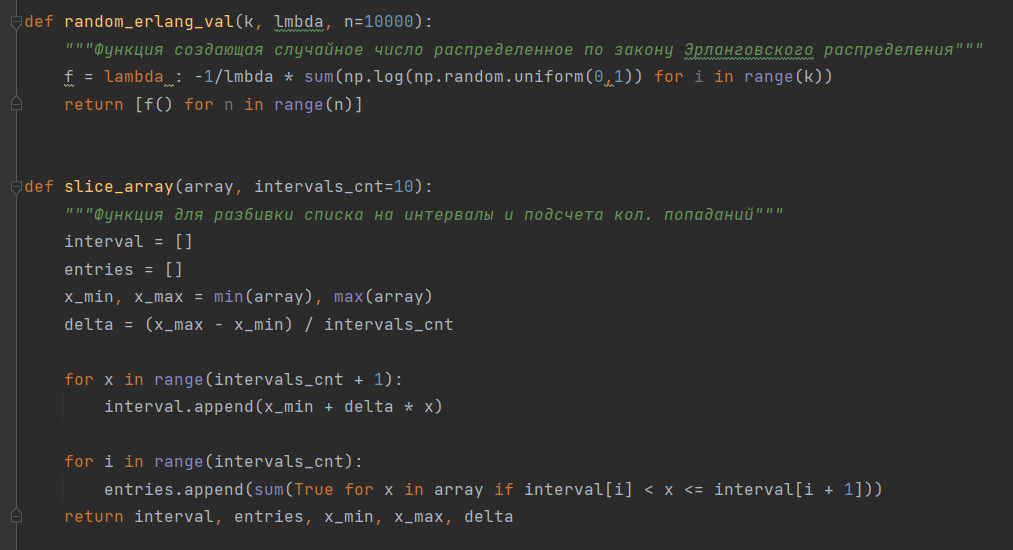
Рисунок 4 – Код программы
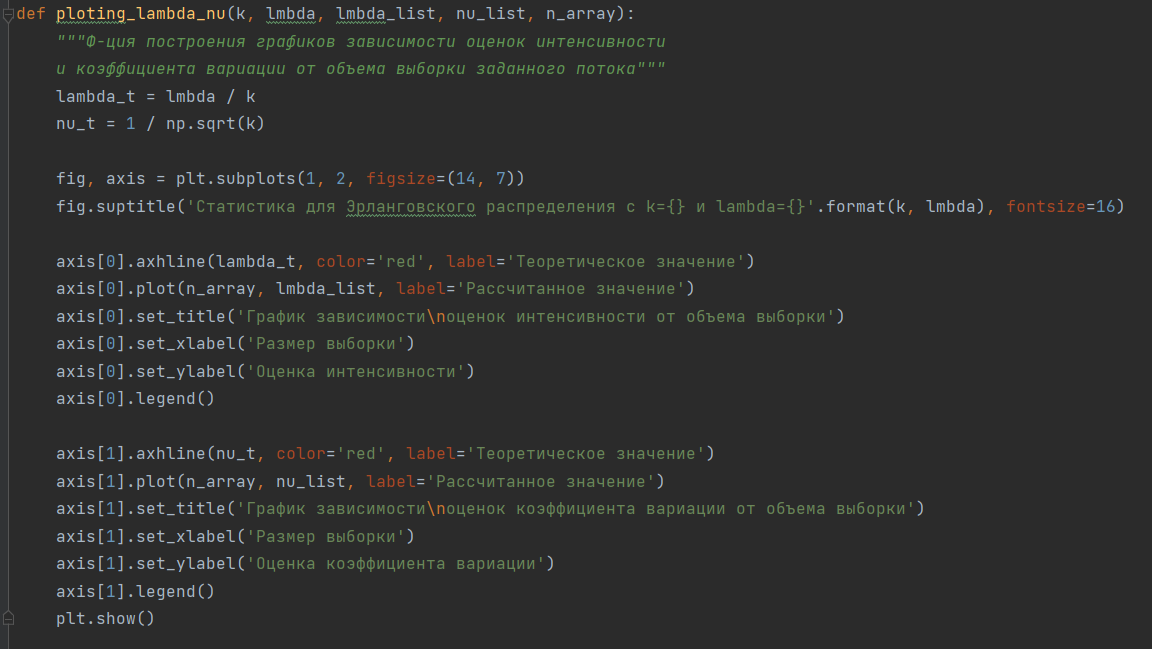
Рисунок 5 – Код программы
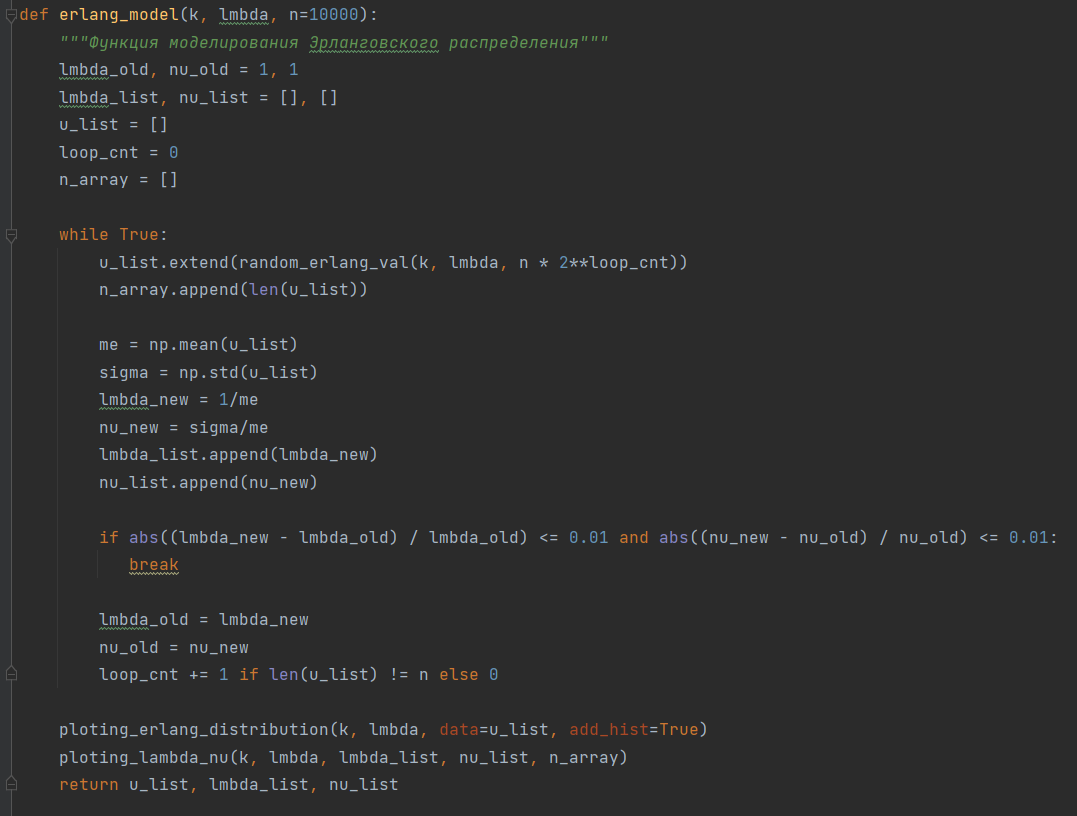
Рисунок 6 – Код программы
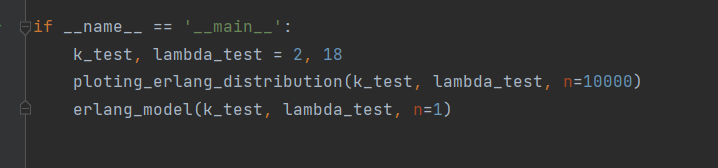
Рисунок 7 – Код программы
График плотности вероятности, построенный по смоделированному Эрлановскому потоку представлен на рисунке 8.
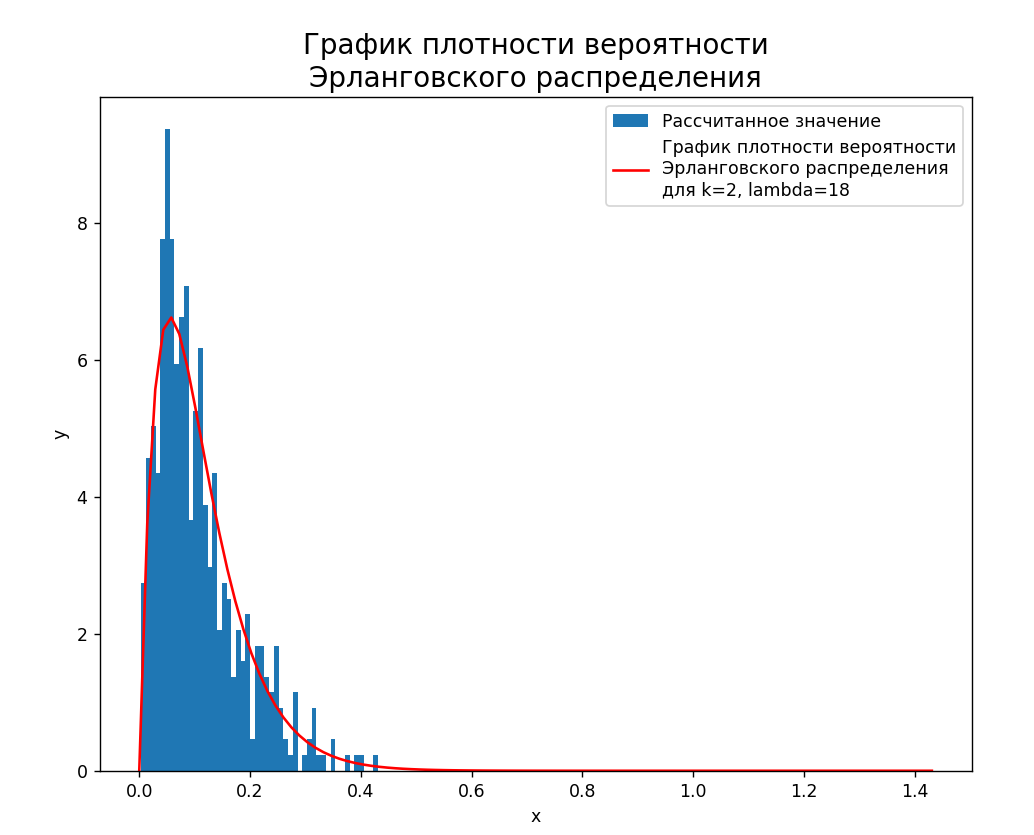
Рисунок 8 – График плотности вероятности
Графики зависимости оценок интенсивности и коэффициента вариации от объема выборки представлены на рисунке 9. Уровнем отмечены теоретические значения эти величин.
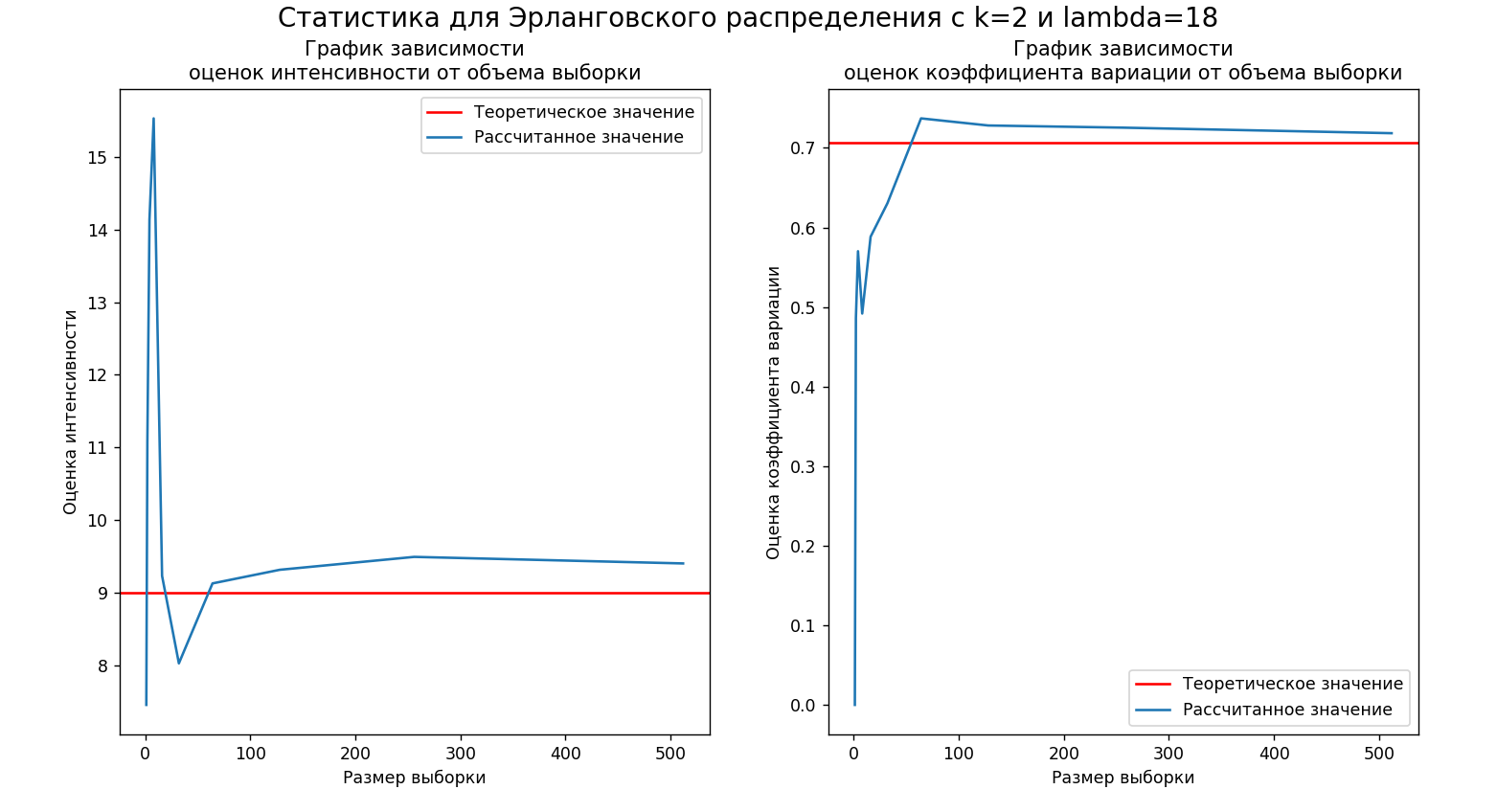 Рисунок
9 – Графики зависимости оценок
интенсивности и коэффициента вариации
Рисунок
9 – Графики зависимости оценок
интенсивности и коэффициента вариации
Вывод
Таким образом, подводя итог ко всем выше проделанным операциям, можно сделать вывод о том, что в ходе выполнения данной лабораторной работы было моделирование стохастического стационарного потока, с эрланговским распределением времени между заявками. Было получено, что экспериментальное значение интенсивности и коэффициента вариации потока с увеличением количества заявок будет стремиться к теоретическим значениям, которые можно рассчитать по соответствующим формулам.
