МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

КАФЕДРА 82

ОЦЕНКА

ПРЕПОДАВАТЕЛЬ

доцент				В. С. Блюм
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ЛАБОРАТОРНАЯ РАБОТА №5

ИНТЕЛЛЕКТУАЛЬНЫЙ АНАЛИЗ ДАННЫХ. МЕТОД ДЕРЕВЬЕВ ПРИНЯТИЯ РЕШЕНИЙ

по дисциплине: Интеллектуальные информационные системы

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	Z9411				А. С. Чурилов
	номер группы		подпись, дата		инициалы, фамилия
Студенческий билет №	2019/3684

Санкт-Петербург 2024

Цель работы: разобрать применения метода принятия решений к заданному набору данных.

Ход работы:

1. Запускаем программу RapidMiner.

2. Открываем во вкладке Repository папку Samples. В Samples откроем папку processes и затем откроем папку 01_Learner (рисунок 1).

Рисунок 1 – Папка 01_Learner

3. Затем в папке 01_Learner откроем файл 01_DecisionTree (рисунок 2).

Рисунок 2 – Файл 01_DecisionTree

Результат приведён на рисунке 3.

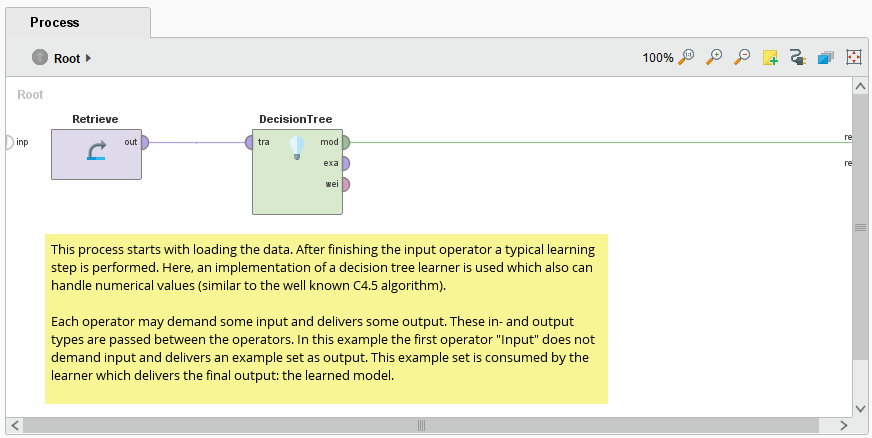
Рисунок 3 – Результат

4. Нажмём кнопку Start и посмотрим результаты (рисунок 4)

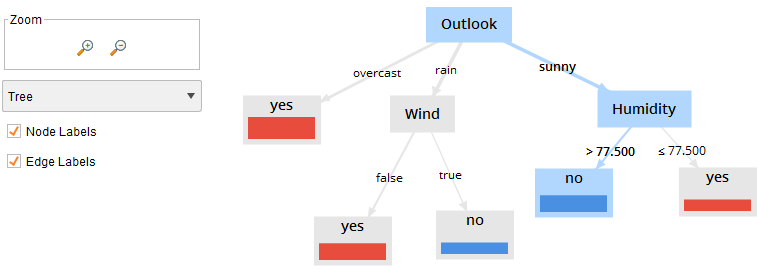
Рисунок 4 – Выполнение процесса

5. Перейдём во вкладку Description (рисунок 5).

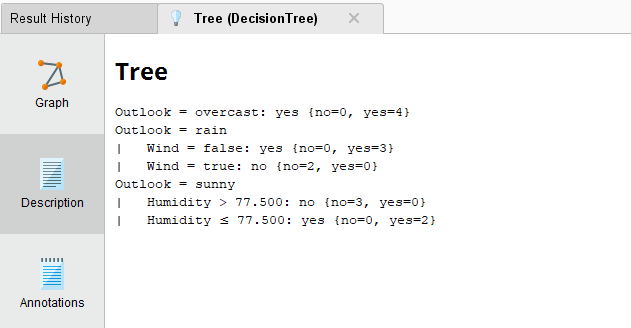
Рисунок 5 – Вкладка Description

6. Вернёмся в вид Design, нажмём на процесс Retrieve ЛКП и увидим список хранилищей (рисунок 6).

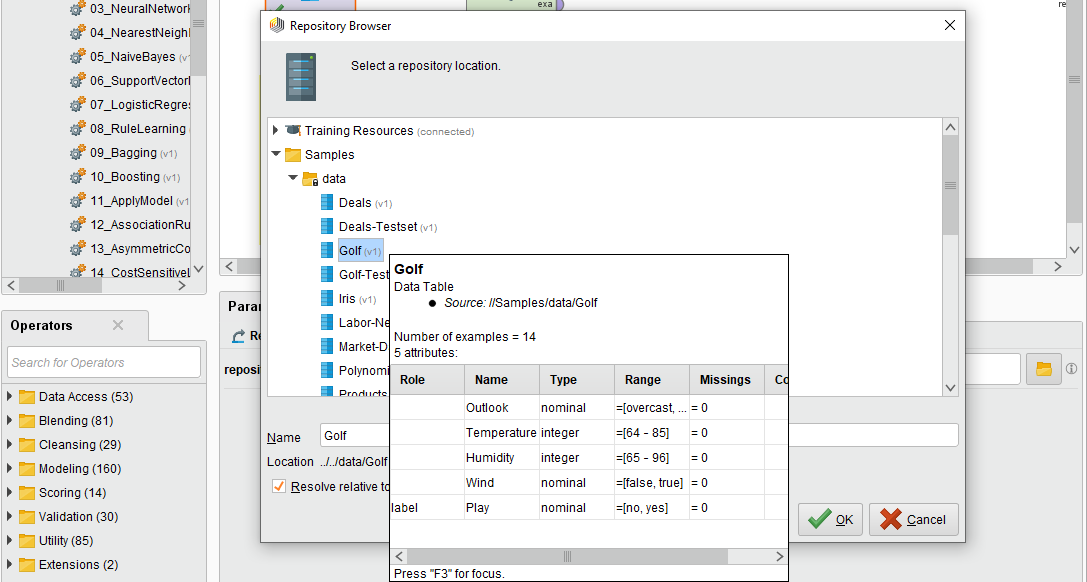
Рисунок 6 - Список хранилищей

7. Откроем Golf (рисунок 7).

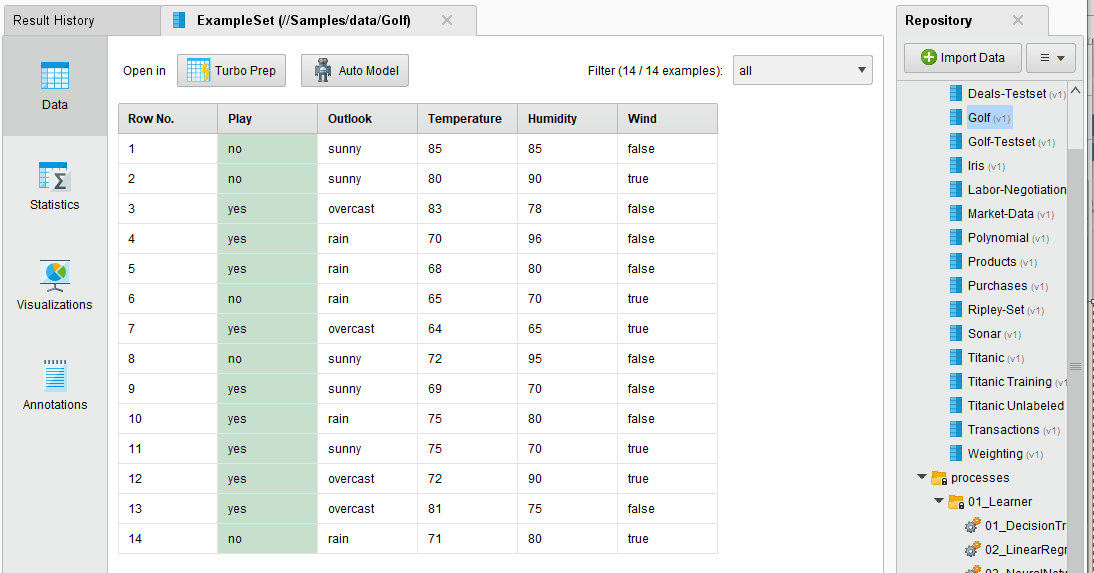
Рисунок 7 - Golf

8. Откроем статистику (рисунок 8).

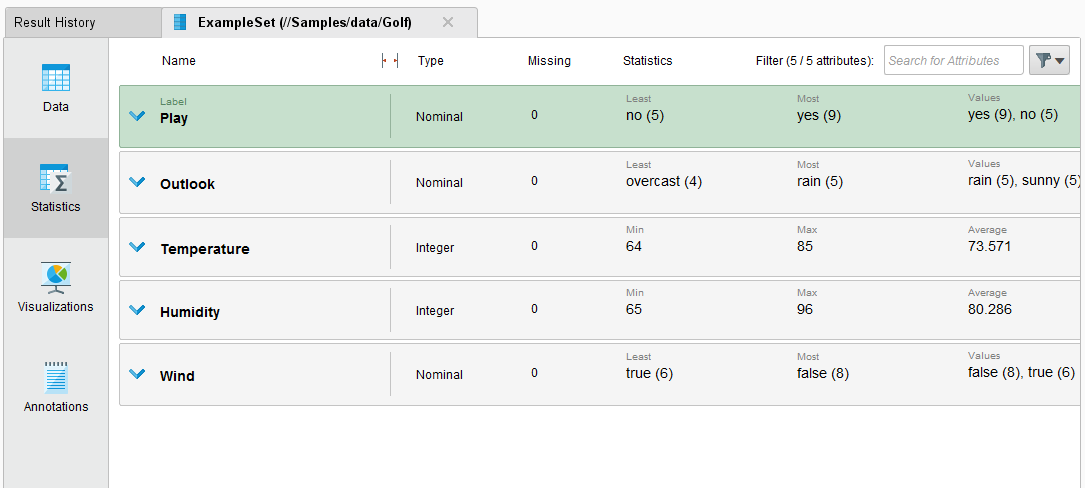
Рисунок 8 - Статистика

9. Добавим модификацию метода принятия решений Decision Stump к Продаже игр.

10. Соединим out с tra и mod c res (рисунок 9).

Рисунок 9 – Соединение с Decision Stump

11. Запустим процесс (рисунок 10).

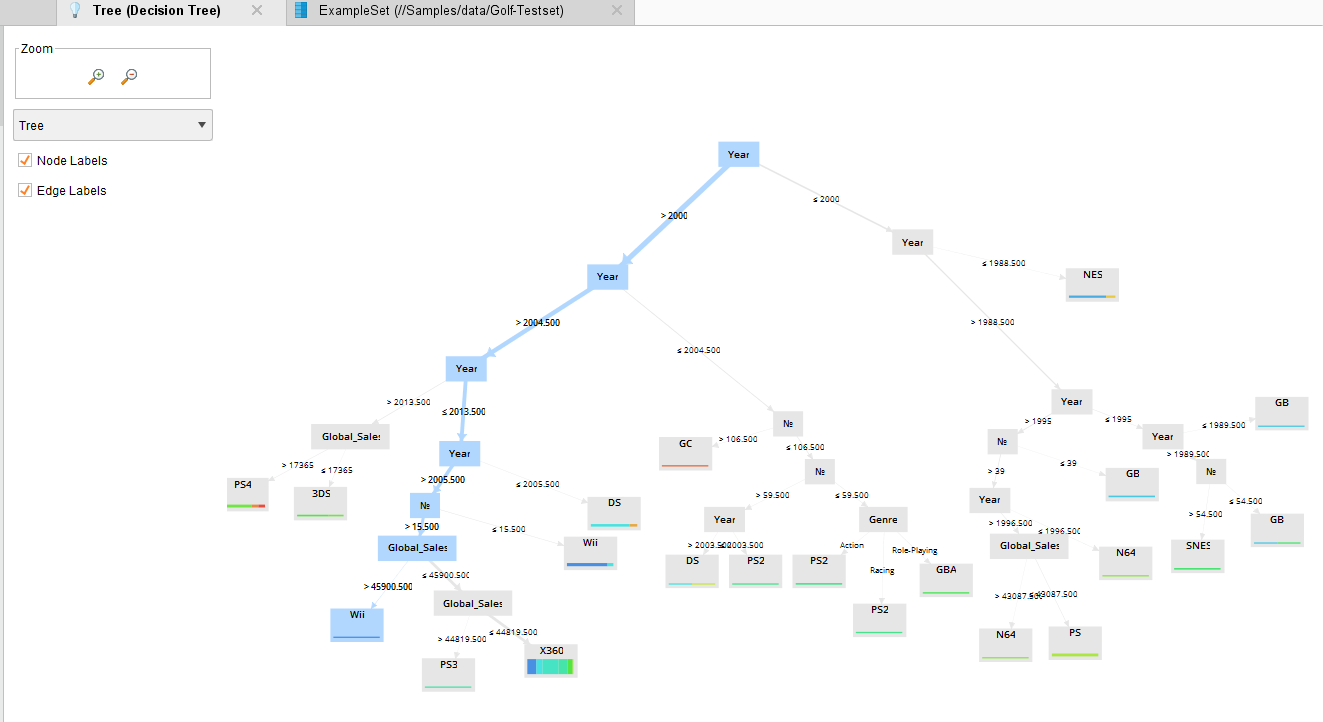
Рисунок 10 – Graph

На примере рисунка 11 видно, что благодаря такому представлению данных моего набора можно легко проследить до нижних уровней соотношение каждого элемента. Например, в промежуток с середины 2013 года по середину 2014 продажи игр на платформе PS4 превысило 17365 тысяч экземпляров (рисунок 11)

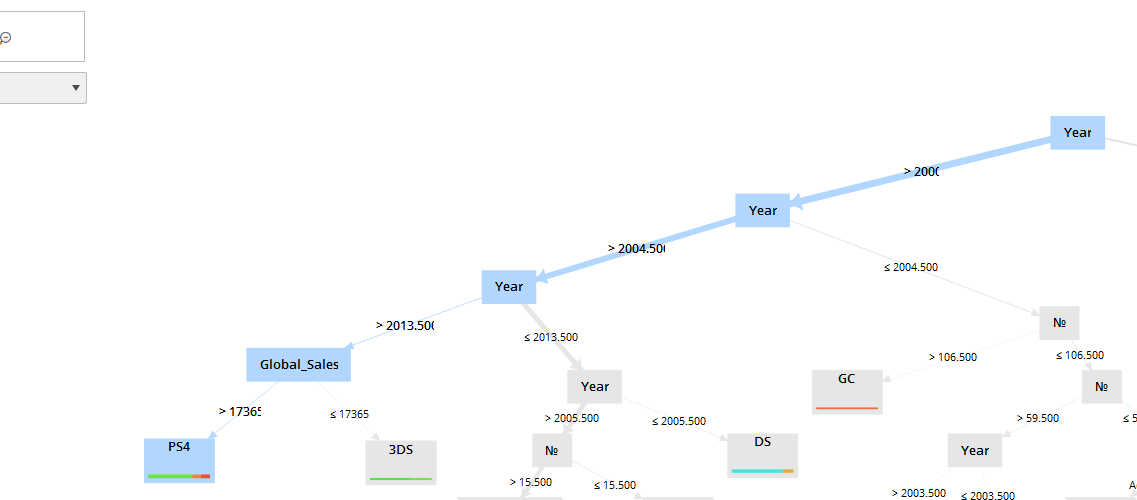
Рисунок 11 – ветвь построенное дерева

12. Перейдём в Description (рисунок 12).

Рисунок 22 – Description

13. Откроем Golf-Testset (рисунок 13).

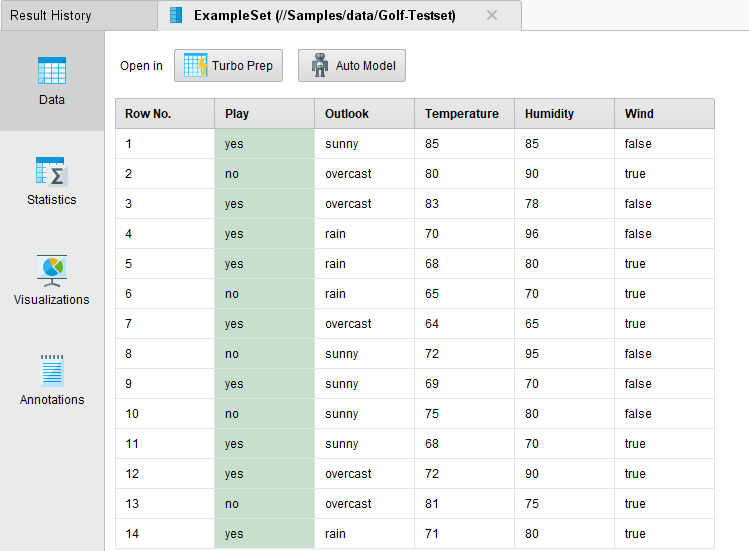
Рисунок 33 – Testset

14. Перейдём в Статистику (рисунок 14).

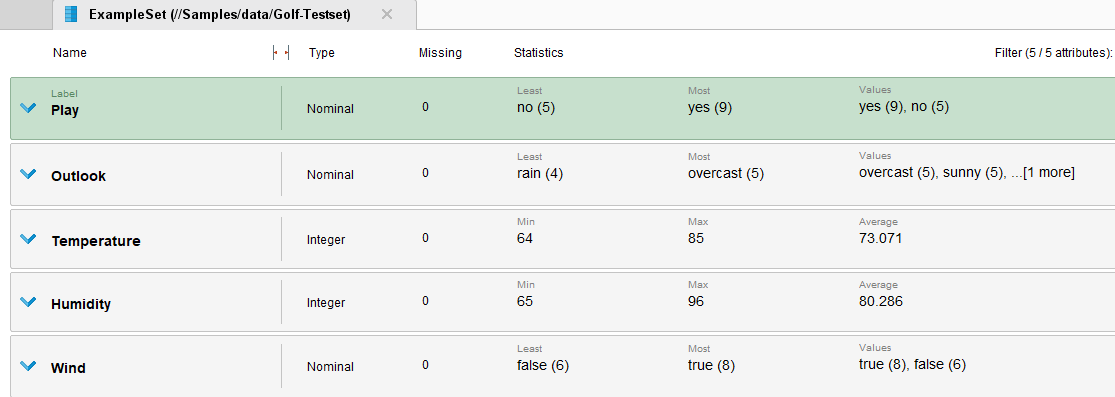
Рисунок 44 – Статистика

Контрольные вопросы

Что такое дерево решений?

Деревья решений – это способ представления правил в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение (рис.15).

Под правилом понимается логическая конструкция, представленная в виде "если ... то ...".

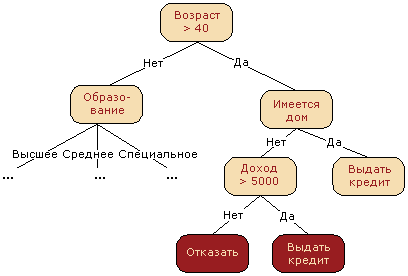
Рисунок 15 – Пример дерева решений

Какие три типа задач решаются методом деревьев решений?

Область применения деревья решений в настоящее время широка, но все задачи, решаемые этим аппаратом, могут быть объединены в следующие три класса:

1. Описание данных: Деревья решений позволяют хранить информацию о данных в компактной форме, вместо них мы можем хранить дерево решений, которое содержит точное описание объектов.

2. Классификация: Деревья решений отлично справляются с задачами классификации, т.е. отнесения объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные значения.

3. Регрессия: если целевая переменная имеет непрерывные значения, деревья решений позволяют установить зависимость целевой переменной от независимых(входных) переменных. Например, к этому классу относятся задачи численного прогнозирования (предсказания значений целевой переменной).

Какие существуют алгоритмы, реализующие деревья решений?

На сегодняшний день существует значительное число алгоритмов, реализующих деревья решений CART, C4.5, NewId, ITrule, CHAID, CN2 и т.д. Но наибольшее распространение и популярность получили следующие два:

CART (Classification and Regression Tree) – это алгоритм построения бинарного дерева решений – дихотомической классификационной модели. Каждый узел дерева при разбиении имеет только двух потомков. Как видно из названия алгоритма, решает задачи классификации и регрессии.

C4.5 – алгоритм построения дерева решений, количество потомков у узла не ограничено. Не умеет работать с непрерывным целевым полем, поэтому решает только задачи классификации.

Большинство из известных алгоритмов являются "жадными алгоритмами". Если один раз был выбран атрибут, и по нему было произведено разбиение на подмножества, то алгоритм не может вернуться назад и выбрать другой атрибут, который дал бы лучшее разбиение. И поэтому на этапе построения нельзя сказать даст ли выбранный атрибут, в конечном итоге, оптимальное разбиение.

Какие критерии разбиения узлов дерева вам известны?

1. Теоретико-информационный критерий

Алгоритм C4.5, усовершенствованная версия алгоритма ID3 (Iterative Dichotomizer), использует теоретико-информационный подход. Для выбора наиболее подходящего атрибута, предлагается следующий критерий:

Gain(X) = Info(T) − Info_z(X) (1)

где Info(T) – энтропия множества T, а

Info_z(T) = 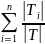* Info(T_i) , (2)

Множества T1, T2, ... Tn получены при разбиении исходного множества T по проверке X. Выбирается атрибут, дающий максимальное значение по критерию (1).

Впервые эта мера была предложена Р. Куинленом в разработанном им алгоритме ID3. Кроме вышеупомянутого алгоритма C4.5, есть еще целый класс алгоритмов, которые используют этот критерий выбора атрибута.

2. Статистический критерий

Алгоритм CART использует так называемый индекс Gini (в честь итальянского экономиста Corrado Gini), который оценивает "расстояние" между распределениями классов.

Gini(c) = 1− 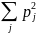, (3)

Где c – текущий узел, а p_j – вероятность класса j в узле c.

CART был предложен Л.Брейманом (L.Breiman) и др.

Преимущества использования деревьев решений?

1. Быстрый процесс обучения;

2. генерация правил в областях, где эксперту трудно формализовать свои знания;

3. извлечение правил на естественном языке;

4. интуитивно понятная классификационная модель;

5. высокая точность прогноза, сопоставимая с другими методами (статистика, нейронные сети);

6. построение непараметрических моделей.

Вывод

В ходе лабораторной работы были изучены основные понятия и принципы работы деревьев решений.

Был проведен анализ данных с использованием метода деревьев решений.

Метод деревьев решений является мощным инструментом для интеллектуального анализа данных. Он предлагает простой и эффективный способ принятия решений, основанный на данных, и может быть применен в широком диапазоне областей, от маркетинга до медицины. Однако, как и любой метод, он имеет свои ограничения и должен использоваться с осторожностью, учитывая возможность переобучения и необходимость правильного подбора параметров.