МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

ПРЕПОДАВАТЕЛЬ

ассистент		Н. В. Апанасенко
должность, уч. степень, звание	подпись, дата	инициалы, фамилия
Лабораторная работа
Анализ элементарной системы множественного доступа
на предмету: Вычислительные системы, сети и телекоммуникации

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	Z9411		А. С. Чурилов
		подпись, дата	инициалы, фамилия

Санкт-Петербург 2023

Цель работы: Получение навыков моделирования алгоритмов случайного множественного доступа в системах передачи данных.

Краткие теоретические сведения:

В данной работе необходимо создать элементарную модель системы множественного доступа, где под множественным доступом подразумевается использование общего канала связи всеми абонентами. Количество абонентов в слоте и количество абонентов, передающих сообщения выбирается случайно. Если передачу проводит один пользователь, то она проходит успешно, если больше одного, то происходит конфликт, и сообщения не пе- редаются, а пользователи осуществляют попытки передать сообщения в следующих слотах, если никто не отправляет сообщение, то система работает в стандартном режиме.

Количество абонентов на слоте k+1:

N_k — количетсво пользователей на слоте,

Р_к — количество пользователей, подключившихся к сети, в данном слоте,

I - индикаторная функция, принимающая значение 1, если R_k = 1, в остальных случаях передает значение 0,

R_k — количество абонентов, передающих сообщений в слоте.

Количество абонентов, передающих значение в слоте k, определяется по биномиальному ₁

закону

(количество пользователей, подключившихся к сети, в данном слоте) распределено по закону Пуассона с параметром Я, находящимся в диапазоне [0.05, 0.5] с шагом 0.05:

Результаты моделирования:

Для данной сети была построена модель Маркова, изображенная на рисунке

1.

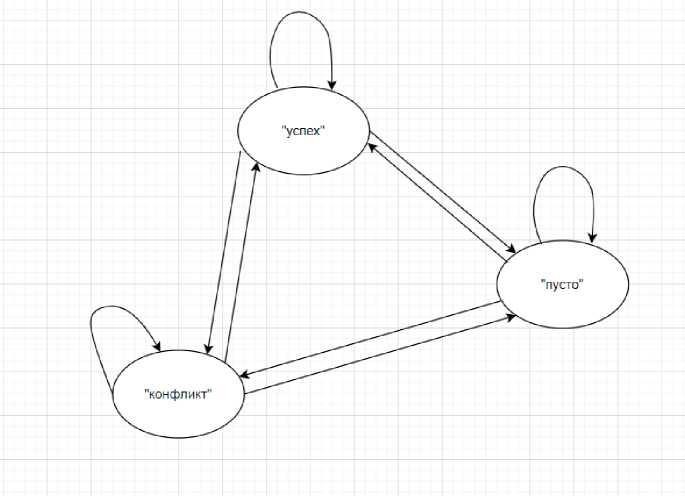
Рисунок 1 - модель Маркова

Из цепи Маркова видно, что прямые переходы можно производить в любое состояние, в обратную же сторону только на одно состояние.

Описание программы:

Создается отдельная функция для биномиального распределения, чтобы находить количество пользователей, передающих сообщения. Если поступающее на вход значение равно 0, то кол-во абонентов, передающих сообщения, равно 0. Если поступающее значение равно 1, то кол-во абонентов, передающих сообщения, равно 1. Если поступающее значение больше 1, то кол-во абонентов, передающих сообщения, будет равно 0, так как произойдет конфликт (сообщения не будут доставлены).

Далее обходятся все значения лямбды с шагом 0,05. Для каждой лямбды получаем количество пользователей, распределённое по закону Пуассона. Затем обходим слоты, чтобы вычислить количество пользователей в слоте. Для первого слота количество пользователей равно первому значению из распределения Пуассона, для остальных слотов, с помощью функции биномиального распределения, находится количество пользователей, пе- редающих сообщение. Затем, основываясь на количестве пользователей, передающих сообщение, вычисляется количество пользователей на слоте. Если сообщение передаёт 1 пользователь, то количество пользователей

определяется как Nk+1 = Nk + Pk - I {Rk = 1}, в остальных случаях как Nk+1

ей в слоте сум

= Nk + Pk. Для каждой лямбды вычисляется сумма пользователей на каждом слоте. Для получения среднего количества пользовател ма

абонентов на каждом слоте делится на количество слотов а среднее количество слотов, необходимых для передачи сообщения одним абонентом находится путём деления среднего количества пользователей на лямбда (T = N/X). По полученным значениям N и T строится графики N от X, T от X.

Были построены графики N от Я (синяя линия), T от Я (бирюзовая линия).

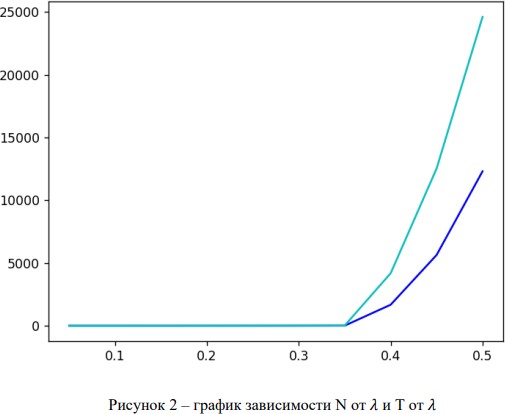
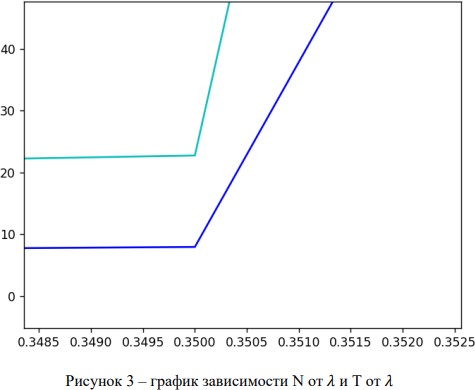
Из рисунка 2 видно, что рост среднего количества абонентов начинает резко увеличиваться c X = 0,35. Такое поведение графика можно объяснить высокой нагрузкой на систему. При большем значении Я возрастает количество пользователей в системе, а вместе с ними и увеличивается количество слотов, необходимых для приема и обработки сообщений от пользователей. На рисунке можно заметить, что с увеличением Я увеличивается разница между средним количеством слотов и средним количеством пользователей в слоте. Значит данная система не выдерживает большого количества пользователей. Из рисунка 3 видно, что для данной генерации чисел, до лямбды = 0,35 , значения N и T остаются неизменными, а именно 8 и 22,8. При таких значениях система справляется с нагрузкой и может стабильно работать только при N = 8 и Т = 22,8. С увеличением значения Я система не справляется с нагрузкой, отчего приходящие пользователи дольше остаются в сети для успешной отправки сообщений, а значит и среднее количество слотов для одного абонента будет расти гораздо быстрее среднего количества абонентов в слоте (разница между линейными графиками на рисунке). На основе графиков можно сделать вывод, что система рассчитана на ограниченное число пользователей.

Вывод:

В результате выполнения лабораторной работы была смоделирована сеть, которая принимает и обрабатывает сообщения пользователей с одним условием, что в определенный момент времени (слот) только один абонент передает сообщение, иначе возникает конфликт в системе. По построенным графикам можно сделать вывод, что система работает стабильно при значении лямбды = 0,35. При возрастании параметра система не справляется с большим количеством пользователей, возрастает время ожидания, чтобы отправить сообщение.

Листинг программы:

from numpy import random, arange import matplotlib.pyplot as plt

# Кол-во слотов в сети S = 100000

# Список значений лямбды lambds = arange(0.05,0.51,0.05)

# Суммарное значение кол-ва пользователей в каждом слоте sum = 0

# Кол-во пользователей в слоте Nk = 0

# Список для среднего кол-ва абонентов n = [ ]

# Список для среднего количества слотов, для передачи сообщения одним абонентом t = [ ]

#создаем функцию для биномиального распределения def binom(x):

try:

# Вычисляем кол-во пользователей, собирающихся передать сообщение Bin=random.binomial(n=x, p=1/x)

except:

# если х = 0, то никто не передаёт сообщения Bin=0

return Bin

def algorithm(S,lambds,sum):

# обходим все значения лямбд for l in lambds:

# получаем Пуассоновское распределение пользователей на каждом слоте Pk=random.poisson(l,S)

# Обходим слоты for i in range(S):

# Описание работы в первом слоте if i==0:

Nk = Pk[0]

sum += Nk

# Описания работы в остальных слотах else:

#получаем кол-во абонентов, собирающихся передать сообщение Rk = binom(Nk)

if Rk==1:

# кол-во абонентов при передаче одним пользователем сообщения Nk=Nk+Pk[i]-1

sum+=Nk

else:

#кол-во абонентов в слоте при кол-ве пользователей, передающих сообщения, не равной 1 Nk=Nk+Pk[i]

# Считаем сумму количества пользователей в каждом слоте sum+=Nk

# Сохраняем N и T n.append((1 / S) * sum) t.append(n[-1] / l)

# Рисуем графики plt.plot(lambds, n, color="b") plt.plot(lambds, t, color="c") plt.show()

algorithm(S, lambds,sum)