
Z9411_Чурилов_ПМО_ЛР
.pdf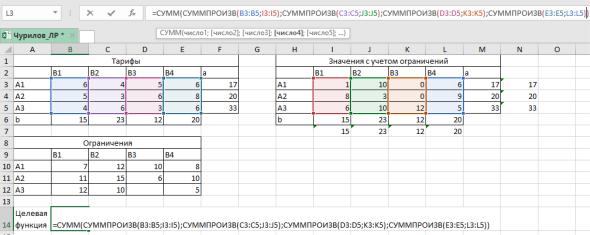
|
|
|
1 |
|
|
10 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2 |
11 |
|
5 |
15 |
|
3 |
6 |
|
6 |
10 |
|
8 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
3 (-) |
|
|
(+) |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А3 |
12 |
|
4 |
10 |
|
6 |
inf |
|
3 |
5 |
|
6 |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
10 |
|
|
12 |
|
|
5 |
|
|
|
|
|
|
|
(+) |
|
|
(-) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bj |
|
15 |
|
23 |
|
12 |
|
20 |
70 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценка свободной клетки равна Δa23 = 6 - 3 + 6 - 3 = 6.
Сформированный опорный план является оптимальным, поскольку отрицательные оценки свободных клеток отсутствуют.
3) Проверим выдвинутое предположение с помощью функции «Поиск решения» приложения MS Excel.
Для этого создадим три таблицы: в одной укажем значения тарифов, во второй – параметры нашего опорного плана с учетом ограничений, в третьей
– сами значения ограничений. Запишем формулу для вычисления целевой функции.
Рисунок 6 – Исходные данные для оптимизации транспортной задачи с ограничениями
Применим функцию «Поиск решения». В открывшемся окне
«Параметры поиска решения» отметим ячейку с целевой функцией, выберем оптимизацию до минимума, укажем клетки для изменения и пропишем
ограничения.
11

Рисунок 7 – Параметры оптимизации опорного плана с ограничениями
Алгоритм функции «Поиск решения» не смог добиться большей оптимизации опорного плана, о чем свидетельствует возникшая ошибка «В
ходе поиска не удалось найти допустимого решения».
Рисунок 8 – Ошибка поиска решения
Соответственно, опорный план, представленный в таблице 9, является оптимальным при заданных ограничениях.
Вывод.
В ходе выполнения работы был закреплен навык построения опорного плана классической транспортной задачи и его оптимизации, а также получен опыт построения и оптимизации опорного плана транспортной задачи с ограничениями на пропускную способность.
12
