
Z9411_Чурилов_ПМО_ЛР
.pdf
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
Кафедра прикладной информатики
ОЦЕНКА
ПРЕПОДАВАТЕЛЬ
ассистент |
_________________ |
Б.К. Акопян |
подпись, дата
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1
Исследование методов решения транспортных задач с
ограничениями
по дисциплине «Прикладные методы оптимизации» Вариант №17
РАБОТУ ВЫПОЛНИЛ |
|
|
|
СТУДЕНТ ГР. |
Z9411 |
________________ |
А.С. Чурилов |
|
|
подпись, дата |
|
Санкт-Петербург 2023г.
Цель работы.
Изучение методов составления опорных планов и оптимизации
решения транспортной задачи с ограничениями на пропускную способность.
Порядок выполнения работы.
1.Построить опорный план исходной задачи БЕЗ учета ограничений любым известным способом и определить его стоимость.
2.Оптимизировать опорный план ТЗ без ограничений; возможно применение инструментария MS Excel.
3.Составить математическую модель задачи с учетом ограничений.
4.Составить опорный план задачи с ограничениями, показывая процесс удаления фиктивных клеток таблицы.
5.Оценить оптимальность полученного опорного плана, используя метод потенциалов.
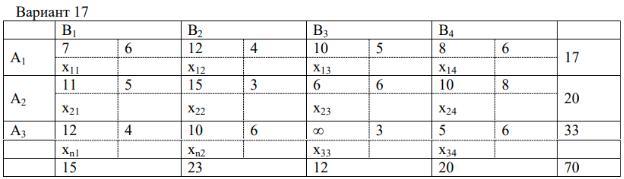
Исходные данные.
Рисунок 1 – Матрица транспортной задачи
Выполнение лабораторной работы.
1. Построить опорный план исходной задачи БЕЗ учета ограничений любым известным способом и определить его стоимость.
Составим исходную таблицу для построения опорного плана без учета ограничений на пропускную способность.
Таблица 1 – Тарифы транспортной задачи без ограничений
|
В1 |
|
В2 |
|
В3 |
В4 |
ai |
||||
|
|
|
|
|
|
|
|
|
|
|
|
А1 |
|
|
6 |
|
4 |
|
|
5 |
|
6 |
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2 |
|
5 |
|
3 |
|
|
6 |
|
|
8 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А3 |
|
4 |
|
6 |
|
|
3 |
|
|
6 |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bj |
15 |
23 |
12 |
|
20 |
|
70 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
Начнём поиск опорного плана методом северо-западного угла (клетка
А1-В1).
1)Сравниваем a1 и b1: a1 = 17, b1 = 15. Значение b1 меньше a1,
записываем в ячейку А1-В1 15; из клетки b1 всё распределили. Для клеток А2-В1 и А3-В1 ничего не осталось, поэтому А2-В1 = 0 и А3-
В1 = 0.
2)Вычитаем a1 – b1 = 17 – 15 = 2. Распределяем остаток в А1-В2. Для клеток А1-В3 и А1-В4 ничего не осталось, так как из а1 всё разместили. Поэтому А1-В3 = 0 и А1-В4 = 0.
3)Так как из а1 и b1 всё распределили, то первую строку и первый
столбец больше не трогаем. Зануляем их.
Таблица 2 – Заполнение первой клетки опорного плана
|
В1 |
В2 |
В3 |
В4 |
ai |
||||
|
|
|
|
|
|
|
|
|
|
А1 |
|
6 |
|
4 |
|
5 |
|
6 |
0 |
|
|
|
|
|
|
|
|
|
|
|
15 |
|
2 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
А2 |
|
5 |
|
3 |
|
6 |
|
8 |
20 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А3 |
|
4 |
|
6 |
|
3 |
|
6 |
33 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bj |
0 |
23 |
12 |
20 |
70 |
||||
|
|
|
|
|
|
|
|
|
|
Таким образом заполняем все клетки в оставшихся строках и столбцах,
пока не распределим все значения ai и bj.
Получили опорный план без учета ограничений. Базисные клетки
3
выделены серым цветом.
Таблица 3 – Опорный план транспортной задачи без ограничений
|
В1 |
В2 |
В3 |
В4 |
ai |
||||
|
|
|
|
|
|
|
|
|
|
А1 |
|
6 |
|
4 |
|
5 |
|
6 |
17 |
|
|
|
|
|
|
|
|
|
|
|
15 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2 |
|
5 |
|
3 |
|
6 |
|
8 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А3 |
|
4 |
|
6 |
|
3 |
|
6 |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
12 |
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
bj |
15 |
23 |
12 |
20 |
70 |
||||
|
|
|
|
|
|
|
|
|
|
Методом северо-западного угла получен план стоимостью: F = 6*15 + 4*2 + 3*20 + 6*1 + 3*12 + 6*20 = 320.
2. Оптимизировать опорный план ТЗ без ограничений; возможно применение инструментария MS Excel.
Используем программу Excel для оптимизации опорного плана.
Для этого создадим две таблицы: в одной укажем значения тарифов, в
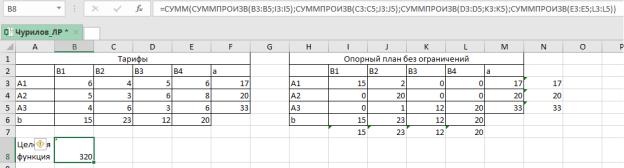
другой – параметры нашего опорного плана. Запишем формулу для вычисления целевой функции.
Рисунок 2 – Исходные данные для оптимизации транспортной задачи без ограничений
Применим функцию «Поиск решения». В открывшемся окне
«Параметры поиска решения» отметим ячейку с целевой функцией, выберем оптимизацию до минимума, укажем клетки для изменения и пропишем
ограничения.
4
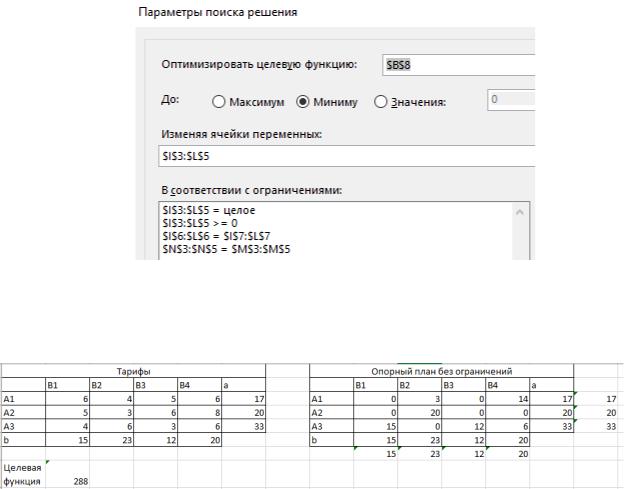
Рисунок 3 – Параметры оптимизации опорного плана без ограничений
В результате оптимизации алгоритм опции «Поиск решения» смог снизить стоимость транспортировки до 288.
Рисунок 4 – Оптимальный план транспортной задачи без ограничений
3. Составить математическую модель задачи с учетом ограничений.
1) Сформулируем математическую модель задачи с ограничениями на
пропускную способность коммуникации. |
|
|
|
|
|
|||||||||
В общем виде: |
|
|
|
|
|
|
|
|
|
|
||||
а) ∑ |
|
= ; |
|
|
|
|
|
|
|
|
|
|||
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) ∑ |
|
= ; |
|
|
|
|
|
|
|
|
|
|||
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) ∑ |
= |
∑ |
; |
|
|
|
|
|
|
|
|
|||
=1 |
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
г) = |
∑ |
|
∑ |
|
|
→ ; |
|
|
|
|
|
|||
|
=1 |
|
=1 |
|
|
|
|
|
|
|
|
|
||
д) 0 ≤ ≤ |
|
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В нашем случае: |
|
|
|
|
|
|
|
|
|
|||||
а) ∑4 |
|
= 17; |
∑4 |
|
= 20; |
∑4 |
|
|
= 33. |
|
||||
=1 |
1 |
|
|
|
|
=1 2 |
|
=1 3 |
|
|
|
|||
б) ∑3 |
|
= 15; |
∑3 |
|
= 23; |
∑3 |
|
= 12; |
∑3 |
= 20. |
||||
=1 |
1 |
|
|
|
|
=1 2 |
|
=1 |
3 |
|
|
=1 |
4 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
в) ∑3=1 = ∑4=1 = 70.
г) = ∑3=1 ∑4=1 → .
д) d11 = 7, d12 = 12, d13 = 10, d14 = 8 и т.д.
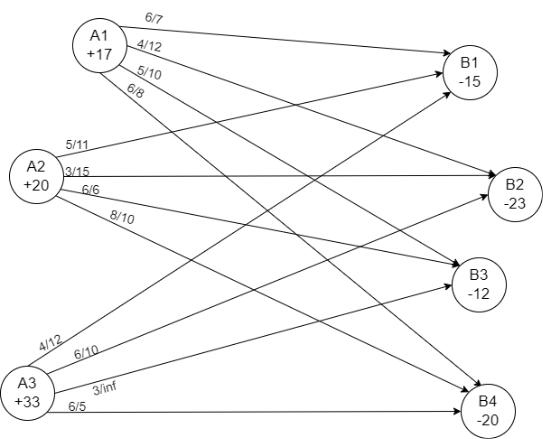
2) Представим исходную транспортную задачу в сетевой форме.
Рисунок 5 – Сетевая форма транспортной задачи с ограничениями
3) Составим опорный план исходной задачи с учетом ограничений.
Построим исходную таблицу для формирования опорного плана с учетом ограничений на пропускную способность.
Таблица 4 – Тарифы транспортной задачи с ограничениями
|
В1 |
|
|
В2 |
|
|
В3 |
|
В4 |
ai |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А1 |
7 |
|
6 |
12 |
|
4 |
|
10 |
|
5 |
8 |
|
6 |
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2 |
11 |
|
5 |
15 |
|
3 |
|
6 |
|
6 |
10 |
|
8 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А3 |
12 |
|
4 |
10 |
|
6 |
|
inf |
|
3 |
5 |
|
6 |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bj |
15 |
23 |
12 |
20 |
70 |
||||
|
|
|
|
|
|
|
|
|
|
Начнём поиск опорного плана методом северо-западного угла (клетка
А1-В1).
1)Сравниваем a1, b1 и d11: a1 = 17, b1 = 15, d11 = 7. Значение d11
наименьшее, записываем в ячейку А1-В1 7.
2)Корректируем клетки a1 и b1. Вычитаем a1 – d11 = 17 – 7 = 10.
Вычитаем b1 – d11 = 15 – 7 = 8.
3)Распределяем остаток в А1-В2. Сравниваем a1, b2 и d12: a1 = 10, b1 = 23, d12 = 12. Значение a1 наименьшее, записываем в ячейку А1-В2
10. Для клеток А1-В3 и А1-В4 ничего не осталось, так как из а1 всё разместили. Поэтому А1-В3 = 0 и А1-В4 = 0. Вычисляем b2 = 23 –
10 = 13.
4)Распределяем остаток в А2-В1. Сравниваем a2, b1 и d21: a2 = 20, b1 = 8, d21 = 11. Значение b1 наименьшее, записываем в ячейку А2-В1
8. Для клетки А3-B1 ничего не осталось, так как из b1 всё
разместили. Поэтому А3-В1 = 0. Вычисляем a2 = 20 – 8 = 12.
Таблица 5 – Заполнение первой клетки опорного плана с учетом ограничения
|
|
В1 |
|
В2 |
|
В3 |
|
В4 |
ai |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А1 |
7 |
|
6 |
12 |
|
4 |
10 |
|
5 |
8 |
|
6 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2 |
11 |
|
5 |
15 |
|
3 |
6 |
|
6 |
10 |
|
8 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А3 |
12 |
|
4 |
10 |
|
6 |
inf |
|
3 |
5 |
|
6 |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bj |
|
0 |
|
13 |
|
12 |
|
20 |
70 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом заполняем все клетки в оставшихся строках и столбцах,
пока не распределим все значения ai и bj.
Получили опорный план с учетом ограничений на пропускную
7
способность транспортировки.
Таблица 6 – Опорный план с учетом ограничений
|
|
В1 |
|
В2 |
|
В3 |
|
В4 |
В5 |
|
ai |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А1 |
7 |
|
6 |
12 |
|
4 |
10 |
|
5 |
8 |
|
6 |
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2 |
11 |
|
5 |
15 |
|
3 |
6 |
|
6 |
10 |
|
8 |
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А3 |
12 |
|
4 |
10 |
|
6 |
inf |
|
3 |
5 |
|
6 |
inf |
|
M |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
12 |
|
|
5 |
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А4 |
|
|
|
|
|
|
|
|
|
inf |
|
M |
inf |
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
bj |
|
15 |
|
23 |
|
12 |
|
20 |
|
|
|
70 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составленный опорный план содержит две фиктивные клетки: А3-В5 и
А4-В4.
4. Составить опорный план задачи с ограничениями, показывая процесс удаления фиктивных клеток таблицы.
1) Обратимся к фиктивной клетке А4-В4. Перебросим из неё 9 единиц товара с помощью следующего цикла: А4-В4 (-9) → А2-В4 (+9) → А2-В2 (-9)
→ А3-В2 (+9) → А3-В5 (-9) → А4-В5 (+9).
Таблица 7 – Преобразование фиктивной клетки А4-В4
|
|
В1 |
|
В2 |
|
В3 |
|
В4 |
В5 |
|
ai |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А1 |
7 |
|
6 |
12 |
|
4 |
10 |
|
5 |
8 |
|
6 |
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2 |
11 |
|
5 |
15 |
|
3 |
6 |
|
6 |
10 |
|
8 |
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
3 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А3 |
12 |
|
4 |
10 |
|
6 |
inf |
|
3 |
5 |
|
6 |
inf |
|
M |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
12 |
|
|
5 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А4 |
|
|
|
|
|
|
|
|
|
inf |
|
M |
inf |
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
bj |
15 |
23 |
12 |
20 |
|
70 |
|
|
|
|
|
|
|
2) Обратимся к фиктивной клетке А3-В5. Перебросим из неё 6 единиц товара с помощью следующего цикла: А3-В5 (-6) → А3-В1 (+6) → А1-В1 (-6)
→ А1-В4 (+6) → А4-В4 (-6) → А4-В5 (+6).
Таблица 8 – Преобразование фиктивной клетки А3-В5
|
|
В1 |
|
В2 |
|
В3 |
|
В4 |
В5 |
|
|
ai |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А1 |
7 |
|
6 |
12 |
|
4 |
10 |
|
5 |
8 |
|
6 |
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
10 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2 |
11 |
|
5 |
15 |
|
3 |
6 |
|
6 |
10 |
|
8 |
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
3 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А3 |
12 |
|
4 |
10 |
|
6 |
inf |
|
3 |
5 |
|
6 |
inf |
|
M |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
10 |
|
|
12 |
|
|
5 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А4 |
|
|
|
|
|
|
|
|
|
inf |
|
M |
inf |
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
bj |
|
15 |
|
23 |
|
12 |
|
20 |
|
|
|
70 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В результате получаем опорный план транспортной задачи без |
|||||||||||||||||
фиктивных клеток. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таблица 9 – Опорный план без фиктивных клеток |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
В1 |
|
В2 |
|
В3 |
|
В4 |
ai |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
А1 |
7 |
|
6 |
12 |
|
4 |
10 |
|
5 |
8 |
|
6 |
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
10 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2 |
11 |
|
5 |
15 |
|
3 |
6 |
|
6 |
10 |
|
8 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
3 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А3 |
12 |
|
4 |
10 |
|
6 |
inf |
|
3 |
5 |
|
6 |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
10 |
|
|
12 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bj |
|
15 |
|
23 |
|
12 |
|
20 |
70 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Методом северо-западного угла с учетом ограничений получен план стоимостью: F = 6*1 + 4*10 + 6*6 + 5*8 + 3*3 + 8*9 + 4*6 + 6*10 + 3*12 + 6*5 = 353.
9
5. Оценить оптимальность полученного опорного плана, используя
метод потенциалов.
1)Проверить оптимальность текущего опорного плана методом потенциалов не представляется возможным, так как в опорном плане недостаточное количество свободных клеток для корректного вычисления потенциалов.
2)Определим, является ли план оптимальным с помощью распределительного метода.
а) Определим оценку для свободной клетки А1-В3. Поставим в неё знак
«+», а в остальных вершинах многоугольника, составленного из базовых ячеек, чередующиеся знаки «-», «+», «-».
Таблица 10 – Оценка свободной клетки А1-В3
|
|
В1 |
|
В2 |
|
В3 |
|
В4 |
ai |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А1 |
7 |
|
6 |
12 |
|
4 |
10 |
|
5 |
8 |
|
6 |
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
10 |
|
|
(+) |
|
|
6 |
|
|
|
|
|
|
|
(-) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2 |
11 |
|
5 |
15 |
|
3 |
6 |
|
6 |
10 |
|
8 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
3 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А3 |
12 |
|
4 |
10 |
|
6 |
inf |
|
3 |
5 |
|
6 |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
10 |
|
|
12 |
|
|
5 |
|
|
|
|
|
|
|
(+) |
|
|
(-) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bj |
|
15 |
|
23 |
|
12 |
|
20 |
70 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценка свободной клетки равна Δa13 = 5 - 3 + 6 - 4 = 4.
б) Определим оценку для свободной клетки А2-В3. Поставим в неё знак «+», а в остальных вершинах многоугольника, составленного из базовых ячеек, чередующиеся знаки «-», «+», «-».
Таблица 11 – Оценка свободной клетки А2-В3
|
В1 |
|
|
В2 |
В3 |
|
|
В4 |
ai |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А1 |
7 |
|
6 |
12 |
|
4 |
10 |
|
5 |
8 |
|
6 |
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
