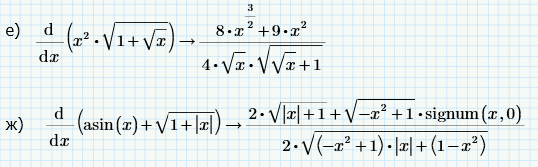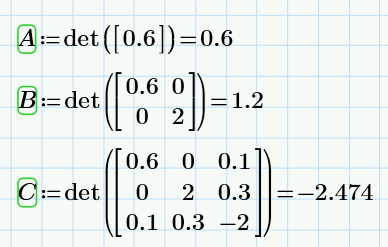Z9411_Чурилов_ПМО_КР
.docxМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
Кафедра прикладной информатики
ОЦЕНКА
ПРЕПОДАВАТЕЛЬ
старший преподаватель _________________ Н.Н. Григорьева
подпись, дата
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Прикладные методы оптимизации»
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ ГР. Z9411 ________________ А. С. Чурилов
подпись, дата
Студенческий билет № 2019/3684
Санкт-Петербург 2023г.
Задание 1.
Вариант 1.
Вычислить производные сложных функций в соответствии с вариантом задания вручную и с использованием среды MathCAD.
|
|
Решение:
Произведём вычисление производных заданных сложных функций вручную.







Проверим себя с помощью пакетного модуля MathCAD
|
|
|
Вывод: в результате решения задачи улучшил свои навыки дифференцирования функций одной переменной; выполнил ручное вычисление производных первого порядка исходных выражений, и проверил полученное решение в программе MathCAD.
Задание 2.
Вариант 7.
Реализовать алгоритмы каждого из описанных методов поиска экстремума функции в указанном интервале с требуемой погрешностью в соответствии с вариантом задания, рассчитать значения критерия оптимальности каждого из алгоритмов
![]()
|
Решение:
Задание 3.
Вариант 7.
Найти градиентным методом экстремум функции нескольких переменных в соответствии с вариантом задания.
![]()
Решение:
Осуществил вручную поиск экстремума функции нескольких переменных аналитически градиентным методом.
Для исходной функции последовательно определил частные производные по переменным x1, x2 и x3.
В результате получил три выражения, каждое из которых, приравняв к нулю, добавил в общую систему. Так как система состоит из трёх уравнений и содержит три неизвестных, то она имеет решение. Поочередно выразил каждый параметр.
Таким образом, определил стационарную точку C (0,378; 0,809; -0,7386).

|
Воспользовавшись MathCAD, проверил составленные математические выкладки и определил, является ли стационарная точка С точкой экстремума функции.
|
|

Составил матрицу Гессе путём вычисления вторых частных производных исходной функции. Так как матрица Гессе симметрична относительно главной диагонали, то достаточно произвести только шесть дифференцирований.
|
|
Вычислил угловые миноры массива М. Для этого воспользовался встроенной функцией det().
|
|
На основе критерия Сильвестра и вычисленных значений угловых миноров пришел к выводу, что матрица Гессе полуопределена, а, следовательно, найденная точка С не является точкой экстремума исходной функции f(x1, x2, x3).
Вывод: в результате решения задачи были улучшены навыки дифференцирования функций нескольких переменных. Было выполнено ручное вычисление частных производных первого порядка и осуществлено определение стационарной точки, а также были найдены частные производные второго порядка, составлена матрица Гессе и рассчитаны её угловые миноры.
Задание 4.
Вариант 5.
Решить задачу оптимизации в среде Excel для функции с учетом заданных по варианту условий.
|
|
Решение.:
Заполнил таблицу для реализации задачи минимизации.
|
|
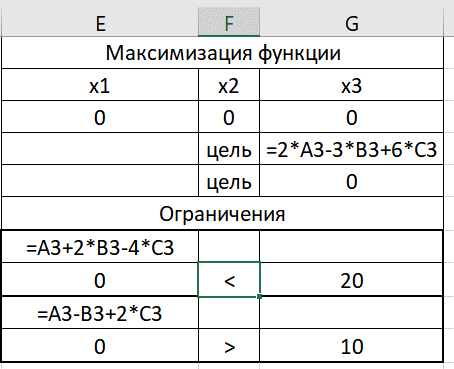
Вызвал функцию «Поиск решения». Заполнил поля.
|
Получили значения, позволяющие осуществить минимизацию исходной функции в соответствии с заданными ограничениями.
|
Заполнил таблицу для реализации задачи минимизации.
|
Вызвал функцию «Поиск решения». Заполнил поля.
|
Получили значения, позволяющие осуществить максимизацию исходной функции в соответствии с заданными ограничениями.
|
|
Вывод: в результате решения задачи получил навыки оптимизации функций с учетом поставленных ограничений. С помощью команды «Поиск решения» реализовал минимизацию и максимизацию исходной функции в программе MS Excel.