МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
КАФЕДРА 41
|
ОЦЕНКА
ПРЕПОДАВАТЕЛЬ
старший преподаватель |
|
|
|
Н. Н. Григорьева |
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
КОНТРОЛЬНАЯ РАБОТА
|
2 вариант
|
по дисциплине: Исследование операций |
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ ГР. № |
Z9411 |
|
|
|
А. С. Чурилов |
|
номер группы |
|
подпись, дата |
|
инициалы, фамилия |
Студенческий билет № |
2019/3084 |
|
|
|
|
Шифр ИНДО |
|
Санкт-Петербург 2023
Вариант 2
Раздел 2 Линейное программирование
1 Решите задачу линейного программирования графическим методом и симплекс-методом
Решение:
Графический метод
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
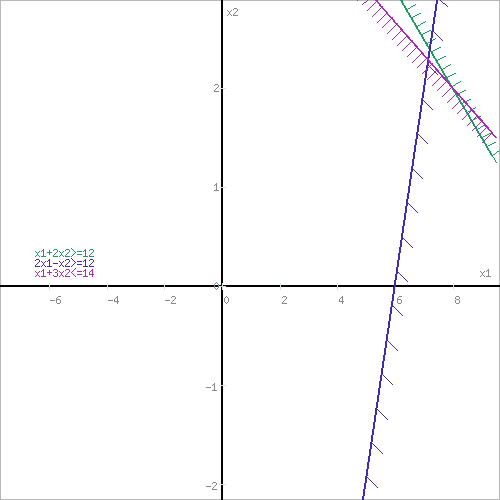
Определим границы области допустимых решений.
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области многоугольника решений.
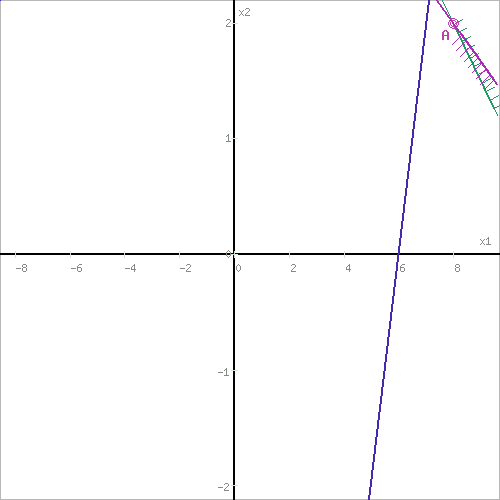
Шаг №3. Рассмотрим целевую функцию задачи F = 3x1+2x2 → min.
Построим прямую, отвечающую значению функции F = 3x1+2x2 = 0.
Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (3;2). Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией.
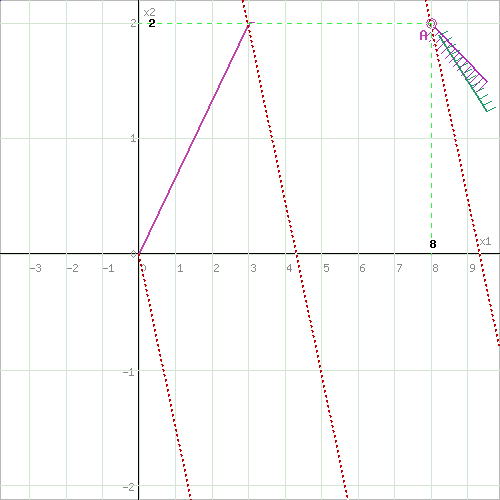
Прямая F(x) = const пересекает область в точке A. Так как точка A получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
x1+2x2=12
x1+3x2=14
Решив систему уравнений, получим: x1 = 8, x2 = 2
Откуда найдем минимальное значение целевой функции:
F(x) = 3*8 + 2*2 = 28
Симплекс-Метод
Решим прямую задачу линейного программирования симплекс-методом.
Определим минимальное значение целевой функции F(X) = 3x1+2x2 при следующих условиях-ограничений.
x1+2x2≥12
2x1-x2≥12
x1+3x2≤14
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла (≥) вводим базисную переменную x3 со знаком минус. В 2-м неравенстве смысла (≥) вводим базисную переменную x4 со знаком минус. В 3-м неравенстве смысла (≤) вводим базисную переменную x5.
x1+2x2-x3 = 12
2x1-x2-x4 = 12
x1+3x2+x5 = 14
Расширенная матрица системы ограничений-равенств данной задачи:
1 |
2 |
-1 |
0 |
0 |
12 |
2 |
-1 |
0 |
-1 |
0 |
12 |
1 |
3 |
0 |
0 |
1 |
14 |
Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x3.
Получаем новую матрицу:
-1 |
-2 |
1 |
0 |
0 |
-12 |
2 |
-1 |
0 |
-1 |
0 |
12 |
1 |
3 |
0 |
0 |
1 |
14 |
2. В качестве базовой переменной можно выбрать x4.
Получаем новую матрицу:
-1 |
-2 |
1 |
0 |
0 |
-12 |
-2 |
1 |
0 |
1 |
0 |
-12 |
1 |
3 |
0 |
0 |
1 |
14 |
3. В качестве базовой переменной можно выбрать x5.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Выразим базисные переменные через остальные:
x3 = x1+2x2-12
x4 = 2x1-x2-12
x5 = -x1-3x2+14
Подставим их в целевую функцию:
F(X) = 3x1+2x2
Среди свободных членов bi имеются отрицательные значения, следовательно, полученный базисный план не является опорным.
Вместо переменной x3 следует ввести переменную x2.
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
Базис |
B |
x1 |
x2 |
x3 |
x4 |
x5 |
x2 |
6 |
0,5 |
1 |
-0,5 |
0 |
0 |
x4 |
-18 |
-2,5 |
0 |
0,5 |
1 |
0 |
x5 |
-4 |
-0,5 |
0 |
1,5 |
0 |
1 |
F(x0) |
-12 |
2 |
0 |
1 |
0 |
0 |
Представим расчет каждого элемента в виде таблицы:
B |
x1 |
x2 |
x3 |
x4 |
x5 |
-12 : -2 |
-1 : -2 |
-2 : -2 |
1 : -2 |
0 : -2 |
0 : -2 |
-12-(-12*1):-2 |
-2-(-1*1):-2 |
1-(-2*1):-2 |
0-(1*1):-2 |
1-(0*1):-2 |
0-(0*1):-2 |
14-(-12*3):-2 |
1-(-1*3):-2 |
3-(-2*3):-2 |
0-(1*3):-2 |
0-(0*3):-2 |
1-(0*3):-2 |
Среди свободных членов bi имеются отрицательные значения, следовательно, полученный базисный план не является опорным.
Вместо переменной x4 следует ввести переменную x1.
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
Базис |
B |
x1 |
x2 |
x3 |
x4 |
x5 |
x2 |
2.4 |
0 |
1 |
-0.4 |
0.2 |
0 |
x4 |
7.2 |
1 |
0 |
-0.2 |
-0.4 |
0 |
x5 |
-0.4 |
0 |
0 |
1.4 |
-0.2 |
1 |
F(x1) |
-26.4 |
0 |
0 |
1.4 |
0.8 |
0 |
Представим расчет каждого элемента в виде таблицы:
B |
x1 |
x2 |
x3 |
x4 |
x5 |
6-(-18*0.5):-2.5 |
0.5-(-2.5*0.5):-2.5 |
1-(0*0.5):-2.5 |
-0.5-(0.5*0.5):-2.5 |
0-(1*0.5):-2.5 |
0-(0*0.5):-2.5 |
-18 : -2.5 |
-2.5 : -2.5 |
0 : -2.5 |
0.5 : -2.5 |
1 : -2.5 |
0 : -2.5 |
-4-(-18*-0.5):-2.5 |
-0.5-(-2.5*-0.5):-2.5 |
0-(0*-0.5):-2.5 |
1.5-(0.5*-0.5):-2.5 |
0-(1*-0.5):-2.5 |
1-(0*-0.5):-2.5 |
Среди свободных членов bi имеются отрицательные значения, следовательно, полученный базисный план не является опорным.
Вместо переменной x5 следует ввести переменную x4.
Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
Базис |
B |
x1 |
x2 |
x3 |
x4 |
x5 |
x2 |
2 |
0 |
1 |
1 |
0 |
1 |
x1 |
8 |
1 |
0 |
-3 |
0 |
-2 |
x4 |
2 |
0 |
0 |
-7 |
1 |
-5 |
F(X2) |
-28 |
0 |
0 |
7 |
0 |
4 |
Представим расчет каждого элемента в виде таблицы:
B |
x1 |
x2 |
x3 |
x4 |
x5 |
2.4-(-0.4*0.2):-0.2 |
0-(0*0.2):-0.2 |
1-(0*0.2):-0.2 |
-0.4-(1.4*0.2):-0.2 |
0.2-(-0.2*0.2):-0.2 |
0-(1*0.2):-0.2 |
7.2-(-0.4*-0.4):-0.2 |
1-(0*-0.4):-0.2 |
0-(0*-0.4):-0.2 |
-0.2-(1.4*-0.4):-0.2 |
-0.4-(-0.2*-0.4):-0.2 |
0-(1*-0.4):-0.2 |
-0.4 : -0.2 |
0 : -0.2 |
0 : -0.2 |
1.4 : -0.2 |
-0.2 : -0.2 |
1 : -0.2 |
Выразим базисные переменные через остальные:
x2 = -x3-x5+2
x1 = 3x3+2x5+8
x4 = 7x3+5x5+2
Подставим их в целевую функцию:
F(X) = 3(3x3+2x5+8)+2(-x3-x5+2)
или
F(X) = 7x3+4x5+28
x2+x3+x5=2
x1-3x3-2x5=8
-7x3+x4-5x5=2
При вычислениях значение Fc = 28 временно не учитываем.
Введем новую переменную x0.
Выразим базисные переменные <2, 1, 4> через небазисные (свободные).
Базисное решение называется допустимым, если оно неотрицательно.
x0 = 0+7x3+4x5
x2 = 2-x3-x5
x1 = 8+3x3+2x5
x4 = 2+7x3+5x5
Переходим к основному алгоритму симплекс-метода.
Поскольку задача решается на минимум, то переменную для включения в текущий план выбирают по минимальному отрицательному числу в уравнении для x0.
Выражение для x0 не содержит отрицательных элементов. Найден оптимальный план.
Окончательный вариант системы уравнений:
x0 = 0+7x3+4x5
x2 = 2-x3-x5
x1 = 8+3x3+2x5
x4 = 2+7x3+5x5
Оптимальный план можно записать так:
x1 = 8, x2 = 2
F(X) = 3*8 + 2*2 = 28