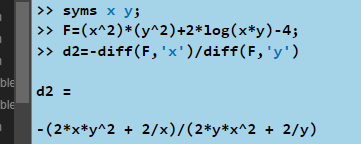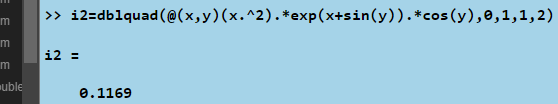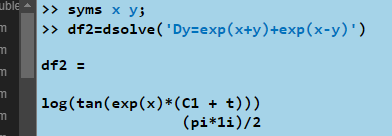Часть 3. Решение типовых задач алгебры и анализа

Упражнение 1.

Для решения заданной системы применим оператор левого деления «\», то есть найдём корни уравнений в виде X=A\B.

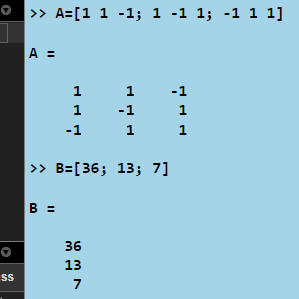
Выпишем матрицы системы A и B. Зададим их элементы с помощью операции конкатенации. Объявление массивов отображено на рисунке 26.

Рисунок 26 – Запись матриц системы линейных уравнений

В рабочем окне программы запишем формулу для нахождения решения уравнений: X=A\B. Результат выполнения операции приведен на рисунке 27.

Рисунок 27 – Применение операции левостороннего деления

Упражнение 2.

Найдём интервалы, где графики функций f1(x) и f2(x) имеют точки пересечения. Выполним их построение в одной области, обратившись к командам plot() и hold on. Для удобства также зададим границы координатных осей.

Составленный набор инструкций имеет вид:

x=-5:5;

f1=-3*x.^3;

f2=x.^4-2*x.^2+10;

plot(x,f1);

hold on;

plot(x,f2);

axis([-5 5 -100 400]);

grid on;

title('Пересечение графиков функций f1(x) и f2(x)');

xlabel('Координатная ось OX');

ylabel('Координатная ось OY');

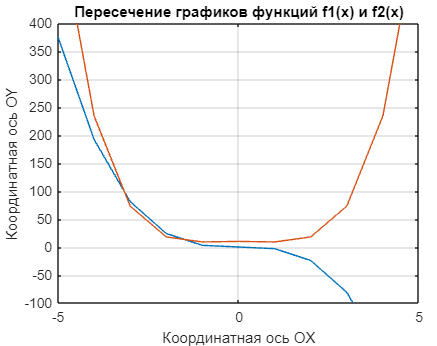
На рисунке 28 показаны две общие точки, которые имеют кривые функций f1(x) и f2(x). Обратившись к иллюстрации, отметим промежутки, где наблюдаются пересечения: [-4; -3] и [-2; -1].

Рисунок 28 – Определение точек пересечения графически

Для определения абсцисс точек пересечения графиков функций f1(x) и f2(x) выведем общее выражение, нули которого будем находить на выделенных интервалах. Требуемая формула имеет вид:

.

Вычислим корни уравнения на двух промежутках с помощью следующих программных инструкций:

x1=fzero('x.^4-2*x.^2+10+3*x.^3', [-4 -3]);

x2=fzero('x.^4-2*x.^2+10+3*x.^3', [-2 -1]);

Полученные численные величины абсцисс общих точек приведены на рисунке 29.

Рисунок 29 – Определение точек пересечения аналитически

Упражнение 3.

Для выполнения символьных вычислений требуется объявить упоминаемые переменные с помощью команды sym(). После задания параметров можно перейти к вычислению предела функции. Оператор, позволяющий реализовать описанное действие, обозначается в среде MATLAB как limit().

На рисунке 30 показан результат нахождения значения предела. Соответствующий численный эквивалент был получен за счет функции double().

Рисунок 30 – Вычисление предела

Упражнение 4.

Определение производной функции, заданной явно, выполним с помощью вызова команды diff(). Результат осуществления отмеченного действия представлен на рисунке 31.

Рисунок 31 – Вычисление производной первой функции

Дифференцирование функции, заданной неявно, производится по специальной формуле:

Опираясь на указанное правило, обратимся к команде diff() дважды, вычисляя производную сначала по переменной x, затем – по переменной y.

Выведенное на экран выражение приведено на рисунке 32.

Рисунок 32 – Вычисление производной второй функции

Упражнение 5.

Найти производную n-го порядка заданной функции в системе MATLAB можно с помощью вызова команды diff() с тремя параметрами: diff(S, 'v', n), где S – дифференцируемое выражение, v – переменная дифференцирования, n – степень дифференцирования.

Выражение, полученное в ходе двукратного дифференцирования указанной в условии функции, приведено на рисунке 33.

Рисунок 33 – Значение второй производной от заданного выражения

Упражнение 6.

Для вычисления определенного интеграла в среде MATLAB разработана команда int(). Пример её применения отображен на рисунке ниже.

Рисунок 34 – Вычисление определенного интеграла

Упражнение 7.

Найдём значение двойного интеграла с помощью функции dblquad(). Результат обращения к данной команде представлен на рисунке 35.

Рисунок 35 – Вычисление двойного интеграла

Упражнение 8.

Первообразная выражения, стоящего под знаком интеграла, легко определяется за счёт использования команды int(), что демонстрируется на рисунке 36.

Рисунок 36 – Вычисление неопределенного интеграла

Упражнение 9.

Для решения дифференциальных уравнений в MATLAB зарезервирована функция dsolve(). Применим её, указав в скобках выражение, задающее уравнение, и начальные условия. На рисунке 37 приведен результат выполнения поставленной задачи.

Рисунок 37 – Решение дифференциального уравнения с начальными условиями

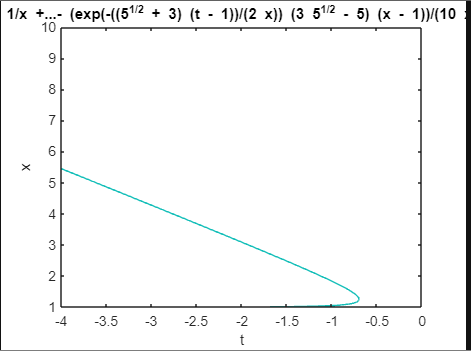
Реализуем построение графика определенной с помощью команды dsolve() функции df1, обратившись к оператору ezplot(). Для координатной оси, связанной с аргументом x, зададим граничные значения [-1; 10] путём использования инструкции axis().

Выполненное построение представлено на рисунке 38.

Рисунок 38 – Построение графика с помощью функции ezplot()

Упражнение 10.

Найдём корни дифференциального уравнения путём вызова функции dsolve(). Результат использования указанной команды отображен на рисунке 39.

Рисунок 39 – Решение дифференциального уравнения