МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
Кафедра прикладной информатики
ОЦЕНКА
ПРЕПОДАВАТЕЛЬ
старший преподаватель _________________ А.В. Сорокин
подпись, дата
ЛАБОРАТОРНАЯ РАБОТА №1
Основы работы в системе matlab Вариант 19
по дисциплине «Моделирование»
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ ГР. Z9411 __________________ А.С. Чурилов
подпись, дата
Студенческий билет № 2019/3684
Санкт-Петербург 2022г.
Оглавление
Выполнение практических заданий 3
Часть 1. Введение в MATLAB 3
Часть 2. Основы работы с MATLAB 5
Часть 3. Решение типовых задач алгебры и анализа 14
Ответы на контрольные вопросы 20
Часть 2. Основы работы с matlab 20
Часть 3. Решение типовых задач алгебры и анализа 24
Заключение 27
Выполнение практических заданий Часть 1. Введение в matlab
Упражнение 1.
Данные для выполнения настоящего раздела лабораторной работы, соответствующие номеру варианта 19, приведены в таблице 1.
Таблица 1 – Материал для варианта №19 |
|
Характеристика |
Значение |
функция y(x) |
|
x1 |
|
xMin |
-2*π |
dx |
|
xMax |
2*π |
Упражнение 2.
В программе MATLAB добавим переменную x0 и укажем её значение.
После определения параметра x0 можно реализовать вычисление значения функции y в данной точке. Полученная величина представлена на рисунке 1.
На приведенной иллюстрации можно заметить, что для записи выражения y были применены тригонометрические функции tan() и sin(), а также ряд стандартных математических операторов.
|
Рисунок 1 – Вычисление значения заданной функции в точке x0 |
Упражнение 3.
Сформируем в программе вектор x, заполненный значениями из диапазона [xMin, xMax] с шагом dx, где xMin=-2π, xMax=2π, dx=π/25. Константная величина π в приложении обозначается как «pi».
На рисунке 2 показан пример создания вектора с помощью оператора двоеточия «:», а также приведено несколько элементов характеристики x.
|
Рисунок 2 – Формирование вектора с помощью оператора двоеточия |
Упражнение 4.
Вычислим значение функции y для каждого элемента вектора x. Для этого запишем выражение для нахождения величины y, заменив операторы, предназначенные для скалярных характеристик, на знаки, подходящие для массивов. В нашем случае к таковым относятся операции деления, умножения и возведения в степень.
На рисунке 3 отображен новый вид формулы, задающей функцию y(x), и несколько вычисленных элементов данного вектора.
|
Рисунок 3 – Вычисление значений функции y для каждого элемента x |
Упражнение 5.
Используя сформированные векторы x и y_x, построим график заданной функции. В текущей ситуации для создания чертежа подходит встроенная команда plot(). Добавление к графику пояснений в виде заголовка и подписей осей возможно с помощью инструкций title(), xlabel() и ylabel().
Запишем программу в среде MATLAB:
plot(x, y_x);
title('График функции y(x)');
xlabel('Координатная ось ОХ');
ylabel('Координатная ось OY');
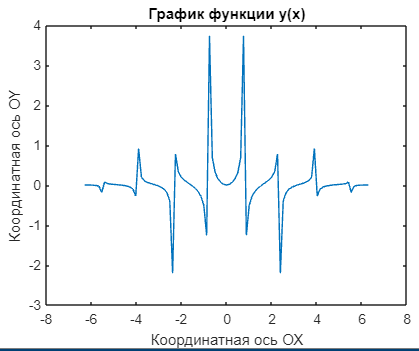
Чертеж, выведенный в графическом окне приложения, представлен на рисунке 4.
|
Рисунок 4 – Построение графика функции по значениям векторов x, y_x |
