Z9411_Чурилов_Стат_КР

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

КАФЕДРА 41

ОЦЕНКА ПРЕПОДАВАТЕЛЬ

канд. физ-мат наук, доцент Е. А. Яковлева

должность, уч. степень, звание подпись, дата инициалы, фамилия

КОНТРОЛЬНАЯ РАБОТА

ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

по дисциплине: СТАТИСТИЧЕСКАЯ ОБРАБОТКА ИНФОРМАЦИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. № Z9411 А.С. Чурилов

^{номер группы} подпись, дата инициалы, фамилия

Студенческий билет № 2019/3684

Шифр ИНДО

____________________________________

Санкт-Петербург 2023

1. Выполнения задания 2.

   1. В программной среде Excel заполняется столбец исходных данных рис. 1. Имеются следующие выборочные данные (выборка 10%-ная, механическая) о выпуске продукции и сумме прибыли, млн. руб.:

Рисунок 1 – Данные о выпуске продукции и сумме прибыли

2. Выполняется сортировка столбца C - прибыль ряда в порядке возрастания. В результате получен новый интервальный ранжированный ряд рис.2.

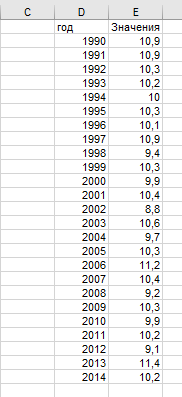
Рисунок 2 – Сортировка данных по прибыли

3. Определяются частоты и частости нового ряда. Для этого используется данные об объеме совокупности исследуемых предприятий N = 25. Дискретный вариационный ряд разбивается на интервалы, число которых подсчитывается по формуле Стержесса

в которой квадратные скобки означают округление числа 5,91, тогда k = 6. Длина частичного интервала определяется по формуле

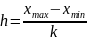
Размах = 𝑥_𝑚𝑎𝑥 − 𝑥_𝑚𝑖𝑛

Среднее значение = сумма x / кол-во измерений (25). Воспользовался функцией Excel

«СРЗНАЧ()» чтобы найти его.

Медиану нашли по значению по середине таблицы. При этом на середине лежало 2 числа: 16,2 и 16,3. В этом случае их сложил и разделил на 2.

Мода – в результатах встречается 3 раза повторяющиеся значения по 2 раза (3 дублета).

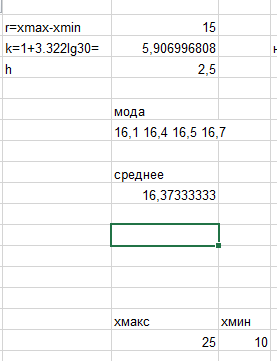
Рисунок 3 – Данные, полученные из таблицы

𝑥_𝑚𝑎𝑥 = 25, 𝑥_𝑚𝑖𝑛 = 10, ℎ = 3. Тогда границы интервалов будут такими: x0=𝑥_𝑚𝑖𝑛=10

x1=𝑥_𝑚𝑖𝑛 + ℎ = 12,5 x2=𝑥_𝑚𝑖𝑛 + 2ℎ = 15 x3=𝑥_𝑚𝑖𝑛 + 3ℎ = 17,5 x4=𝑥_𝑚𝑖𝑛 + 4ℎ = 20 x5=𝑥_𝑚𝑖𝑛 + 5ℎ = 22,5 x6=𝑥_𝑚𝑖𝑛 + 6ℎ = 25

Исключим выброс и получим шаг 1.6 вместо 2,5

Подсчитывается количество предприятий, принадлежащих каждому из интервалов. Вычисляется накопленная частота и процентное отношение частоты к общему объему всей совокупности N = 30 или частость.

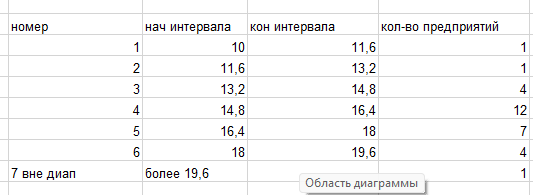
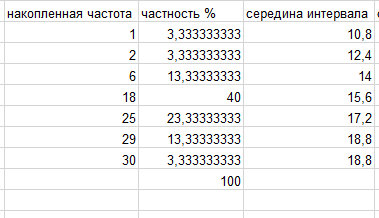Рисунок 3 – Статистический ряд распределения предприятий Значения были найдены следующим образом:

Частность: Кол-во предприятий (n) / общее количество предприятий (N) * 100% Середина интервала: (Начало интервала + Конец интервала) / 2

По данной таблице построил следующие графики (рис.4-6)

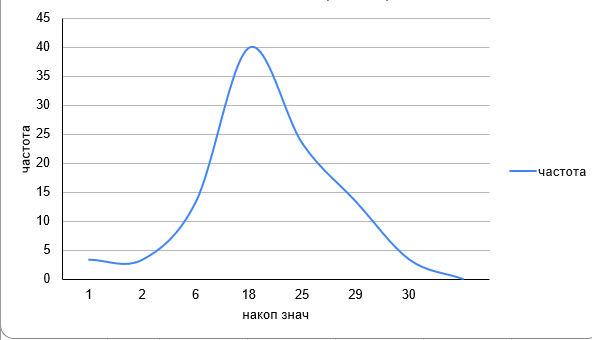
Рисунок 4 – Кривая ненормированной плотности распределения

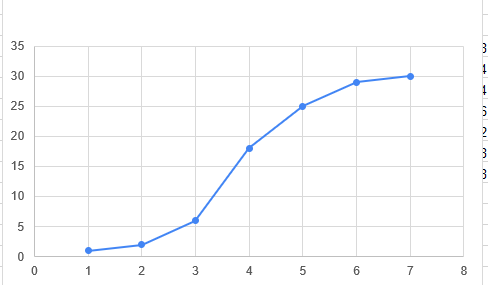
Рисунок 5 – Кумулятивная кривая накопленных частот

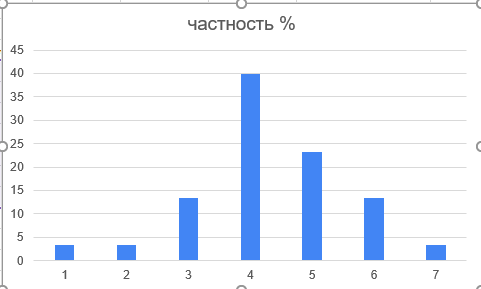
Рисунок 6 – Гистограмма

4. Используя χ2-критерий Пирсона, при уровне значимости α=0,05 проверил гипотезу о том, что случайная величина X – сумма прибыли – распределена по нормальному закону.

Сначала рассчитаем среднее значение сгруппированного ряда, дисперсию и среднее квадратичное отклонение.

Среднее значение сгруппированного ряда =

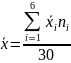
Дисперсия = ;

Среднее квадратичное отклонение =

Результат расчётов представлен на рисунке 7.

Рисунок 7 – Расчёт среднего значения сгруппированного ряда, дисперсии и сигмы

Затем была создана новая таблица, в которую перенесли из предыдущей номера групп и количество элементов(предприятий) в каждой группе.

Опираясь на данные сведения, вычислим следующие характеристики:

- , где 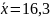и σ = 1,89;

- функция Гаусса: ;

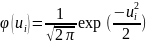- , где N = 30 и h = 1,6;

- .

Получим таблицу, представленную на рисунке 8.

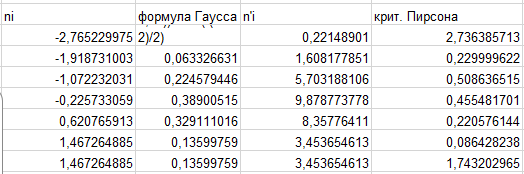
Рисунок 8 – Таблица для проверки распределения по нормальному закону Сравним полученные результаты с теоретическими, используя критерий Пирсона:

По таблице критических точек распределения χ² по уровню значимости α = 0,05 и числу ^{степеней свободы k = 7 - 2 - 1 = 4, находим χ2}кр ^{= 9,5}

Так как:

^χ2табл ^{= 5,9807,}

^χ2кр ^{= 9,5, χ2}табл ^{< χ2}кр

• то выходит, что наша гипотеза о нормальном распределении выполняется с данными результатами.

5. Установил наличие и характер корреляционной связи между стоимостью произведённой продукции (X) и суммой прибыли на одно предприятие (Y). Построил диаграмму рассеяния и линию регрессии.

Используя изначальные данные для 2-го задания – отсортировал значения по выпуске продукции и обозначил их за «x», прибыль обозначил за «y».

С помощью стандартной надстройки Excel «Пакет анализа» построил точечную диаграмму по x и y, построил линейную линию тренда, включил показ уравнения на диаграмме и поместил на диаграмму величину достоверности аппроксимации (R²). Результат представлен на рисунке 9.

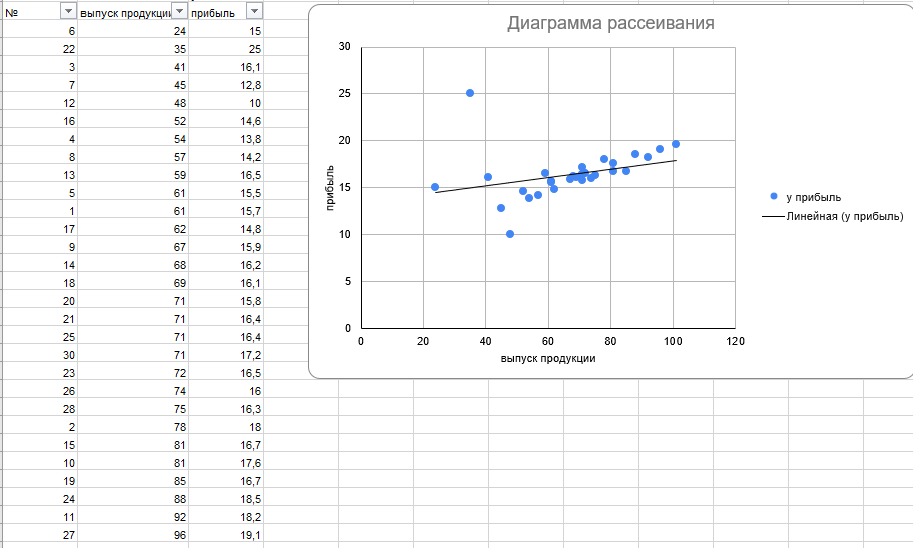
Рисунок 9 – Поле корреляции Получилось выборочное уравнение регрессии: y = 0,0448x + 13,371 R² = 0,1024.

Коэффициент детерминации показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных.

Коэффициент детерминации получился довольно слабым. Для того чтобы улучшить результаты удалим сильно отдалённые результаты от линии тренда – так называемые

«выбросы», которые портят график. В результате получилась таблица, представленная на рисунке 10.

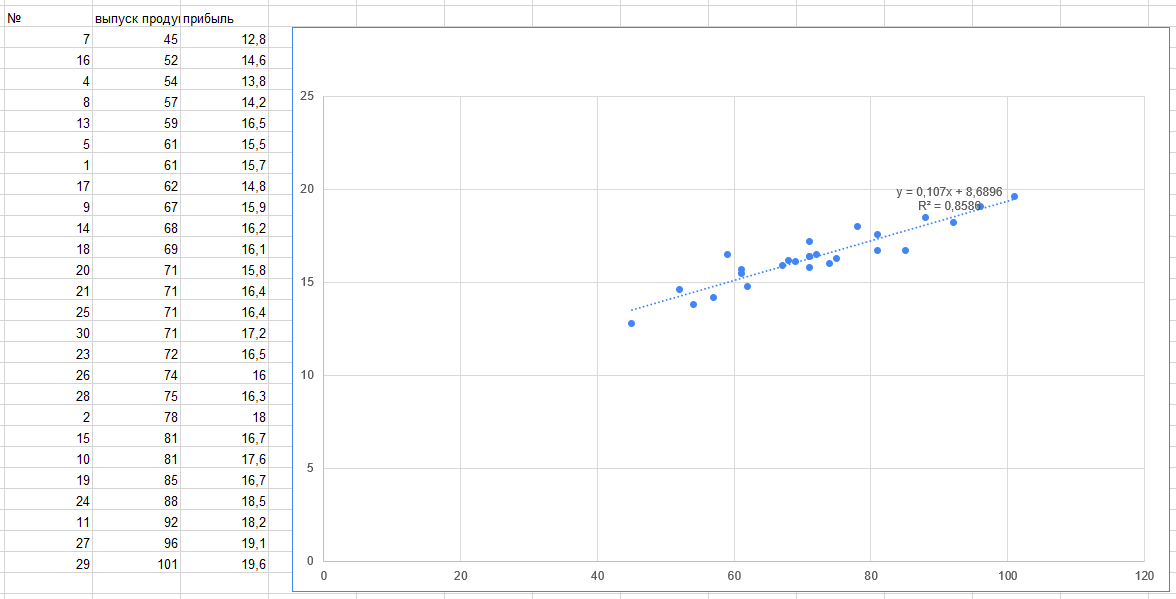
Рисунок 10 – Поле корреляции после удаления выбросов

Теперь выборочное уравнение регрессии: y = 0,107x + 8,6896

. Коэффициент детерминации R² = 0,8586. a = 0,0448

b = 0,107

Коэффициент детерминации объясняет ~50% переменных, объясняемые рассматриваемым уравнением.

6. Рассчитал линейный коэффициент корреляции. Линейный коэффициент корреляции: 𝑟_𝑥𝑦 = √𝑅² = 0,9266

Таким образом, линейная связь между выпуском продукции и величиной прибыли весьма

сильная, т.к. 𝑟_𝑥𝑦 = 0,9266 > 0,7.

Благодаря вычислительным возможностям функции Анализ данных, в программе были найдены предсказанные значения 𝑦̂ и остатки (y-𝑦̂). На основе этих сведений были построены следующие графики:

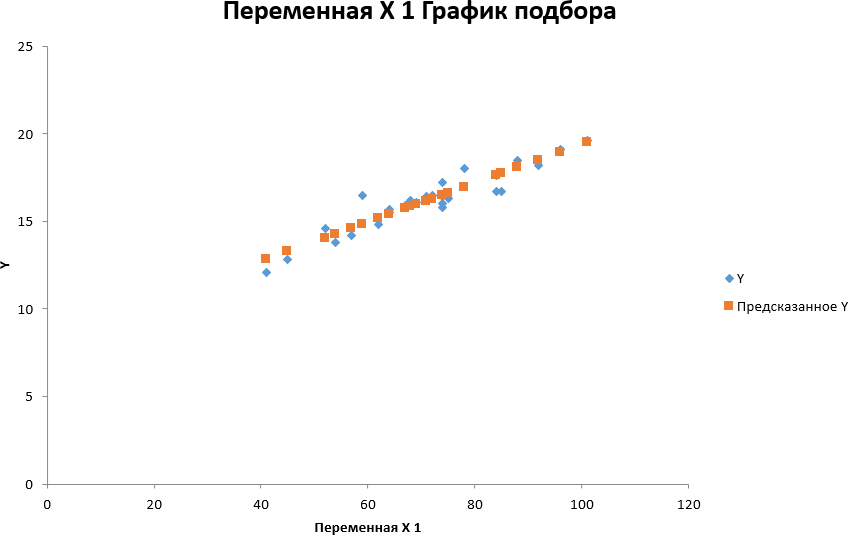
Рисунок 11 - Распределение заданных значений y и предсказанных значений 𝑦̂

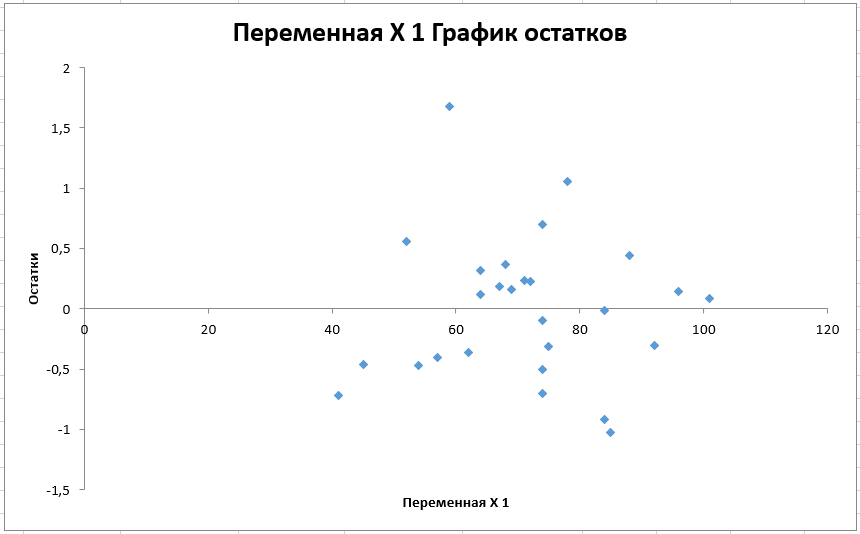
Рисунок 12 - Распределение остаточных значений (y-𝑦̂)

Охарактеризуем статистическую надежность результатов регрессионного анализа с использованием F-критерия Фишера при уровне значимости α = 0,05.

Найдём расчетное значение критерия:

.

Сравнив это значение с табличным получается, что:

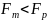
Следовательно, уравнение регрессии является статистически значимым, надежным.

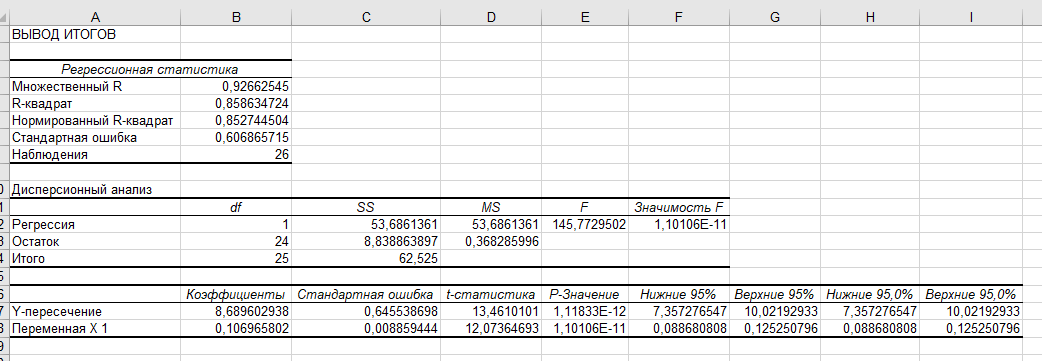
Рисунок 13 – Вывод итогов регрессии

Вывод:

В заключение следует отметить, что задача по анализу данных о прибыли выборки из 30 предприятий с помощью программы Excel и статистических методов была выполнена. Данные были отсортированы, определены частоты и интервалы, рассчитаны различные статистические показатели, такие как диапазон, среднее, медиана и мода.

Гипотеза о нормальном распределении данных была проверена с помощью χ2-критерия ^{Пирсона, и она была признана удовлетворительной при уровне значимости α = 0,05. χ2}набл ^{< χ2}кр

Также были рассчитаны среднее значение, дисперсия и стандартное отклонение сгруппированных данных. 𝑥̅ =16,02666667, 𝐷_𝑥 =3,572622222, 𝜎 =1,890138149.

Корреляция между стоимостью продукции и прибылью также была определена как положительная и сильная, т.к. график растёт и коэффициент корреляции r=0,939 что указывает на сильную связь между этими двумя переменными, т.к. 0,939 > 0,7.

Уравнение регрессии: y = 0,107x + 8,6896

Расчётный F-критерия Фишера 𝐹_р = 187,06 оказался больше табличного значения 𝐹_т, что свидетельствует о том, что уравнение регрессии является статистически значимым, надежным.

В целом, задача была успешно решена, поскольку был проведен тщательный анализ данных о прибыли по выборке предприятий.

2. Задание 3.

7 вариант 7 месяц за 1990-2014 года

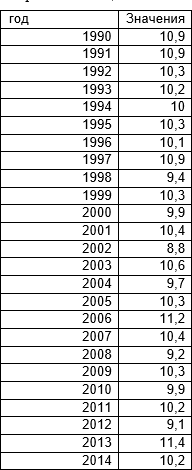
Рисунок 14 – Данные о температуре поверхности океана

1. Выделение и анализ тренда временного ряда.

   1. с помощью метода наименьших квадратов рассчитать линейное уравнение трендовой составляющей

Т(t) = a0 +a1

где t – время.

Задача - построить график распределения температуры на основе исходных данных. Мы наложим линию регрессии на отмеченные значения и выразим уравнение построенной линии.

Рисунок 15 – График распределения температуры

Как видно из приведенного выше рисунка, анализ ряда этим методом не дает удовлетворительных результатов.

2. вычислить коэффициент корреляции (r), его стандартную ошибку (σr), коэффициент детерминации (R²=r² ), который показывает вклад тренда в описание дисперсии исходного ряда.

Будем копировать значения из таблицы – первый ряд без последнего результата, второй ряд рядом – без первого результата. Далее первый ряд без последних двух результатов, второй ряд рядом – без первых двух результатов и так далее. В результате чего получится несколько «дублетов» таких рядов без первых и последних значений.

Для каждых из этих «дублетов» рядов определяем коэффициент корреляции с помощью стандартного пакета анализа в Excel.

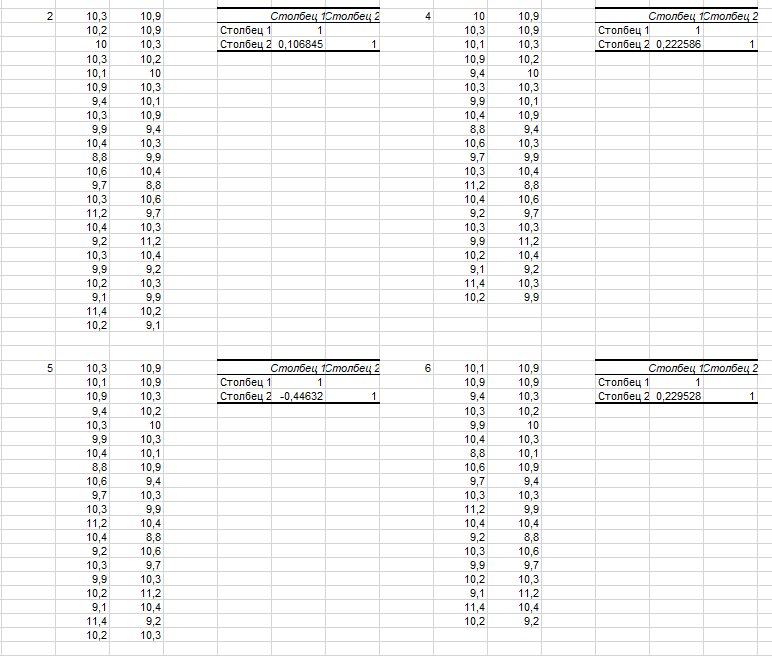
Рисунок 16 – Дублеты рядов

В результате было найдено 12 коэффициентов корреляции. Заносим их в один столбец, строим график и ищем вершины (максимумы) для определения наиболее подходящего значения амплитуды.

В данном случае наиболее подходящий период колебаний равен 12.

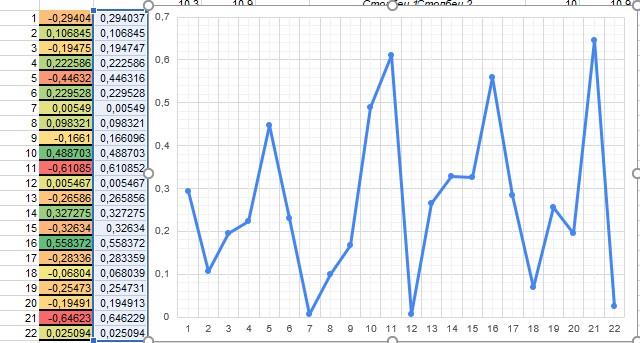
Рисунок 17 – Определение периода колебаний

2. Выведем уравнение, описывающее исходный временной ряд, путём применения функции Фурье, стандартный вид которой записывается следующим образом:

Дополним исходную таблицу дополнительными вычислениями со значениями ^{переменной t}1^{, проходящей полный круг (2π) с шагом 2π/12.}

Определим значения коэффициентов a₀, a₁ и b₁, входящих в первое гармоническое уравнение 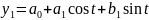(k = 1), по следующим формулам: , , .

Вычислим значения столбца y₁, опираясь на выражение, указанное выше. Также найдём значение ошибки, определяемое по формуле: , где 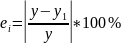. Приближение можно считать достаточным, если соблюдается условие: E < 5%.

Рисунок 18 – Таблица первой гармоники

^{По найденным значениям получаем величину ошибки E}1 ^{= 4.596%.}

^{Так как E}1 ^{< 5%, то делаем вывод, что первого приближения в нашем случае достаточно} для выделения уравнения временного ряда.

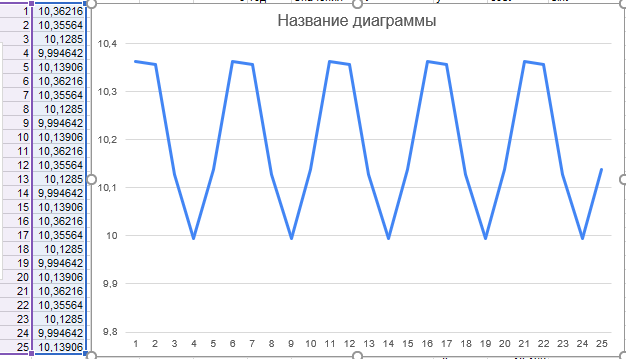^{Построим график распределения найденных значений y}1^.

Рисунок 19 – График первой гармоники

3. Попробуем уменьшить процент ошибки продолжением определения гармоники 2-го уровня.

^{Формулы остаются теми же, однако T заменяется на 2*T. А y}2^=y1^{+𝑎2 cos 2𝑡 + 𝑏2 sin 2𝑡.}

Рисунок 20 – Вторая гармоника

К сожалению, процент ошибки увеличился, попробуем продолжать решать гармонические уравнения, стремясь уменьшить ошибку.

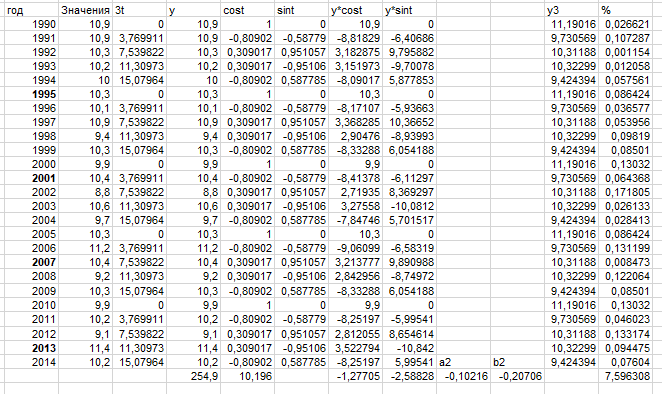
Рисунок 21 – Третья гармоника

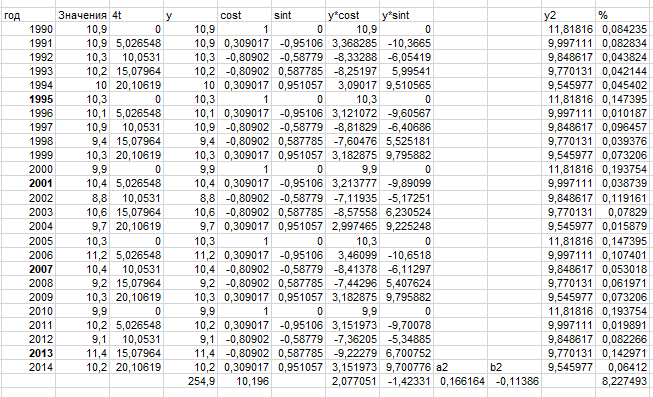
Рисунок 22 – Четвёртая гармоника

Как видно из результатов – процент ошибки E только растёт. После четвёртой гармоники E4=8.22 > 5%.

Попробуем вернуться к началу и изучать гармонику с периодом колебаний равным 6.

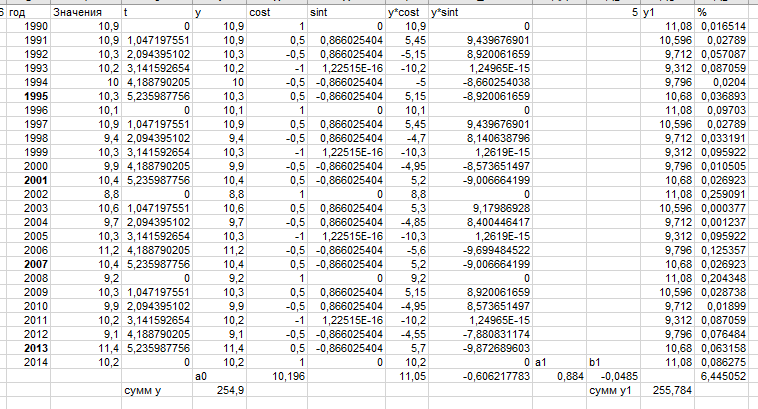
Рисунок 23 – Первая гармоника с периодом колебаний 6

Рисунок 24 - Вторая гармоника с периодом колебаний 6 К сожалению, и здесь процент ошибки растёт.

Возможно, что в наших данных содержатся аномалии, которые влияют на нашу обработку данных.

Попробуем проанализировать данные с помощью метода и избавиться от аномалий.

Для исходных данных рассчитываем среднее квадратичное отклонение, это сигма: σ = 0,628808397.

^λi ^{= |y}i-1^-yi^{|/ σ}

У нас количество измерений = 25, для этого количества критическое значение лямбды является 1,25. Все значения лямбд сравниваются и отмечаются.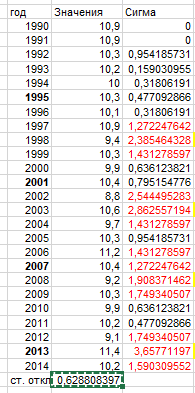

Рисунок 25 – Поиск аномалий

Было найдено несколько аномалий. Избавляемся от них – работаем с данными (y значениями), при этом мы можем избавляться от одиночных аномалий путём приравнивания соседних значений и разделения их на 2, если аномалия одиночная. В случае групп аномалий – находим самую большую и только её приравниваем к среднему значению соседних.

Новые значения заменяем, старые переносим из предыдущей таблицы.

В результате 4-х итераций аномалии так и остались, от них не получилось избавиться.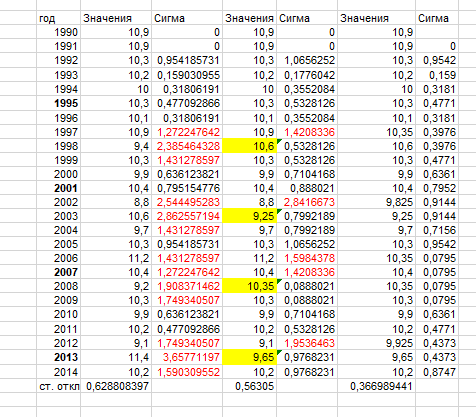

Рисунок 26 – Попытка устранения аномалий

Все аномалии были устранены

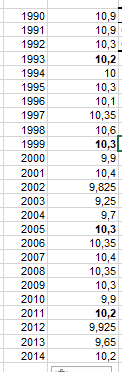
Рисунок 27 – Новая таблица данных

По аналогии с предыдущими данными, была проделана обработка информации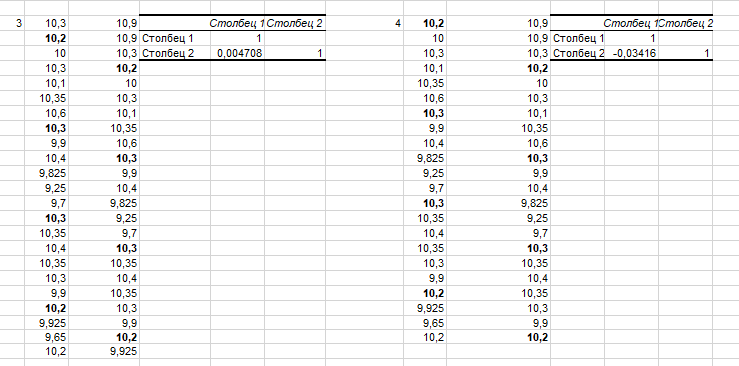

Рисунок 28 – «Дублеты» рядов новой таблицы

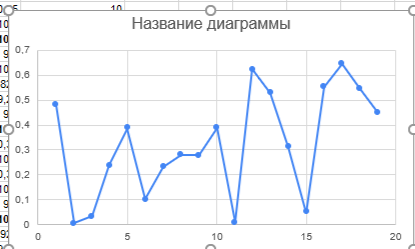Амплитуда равна 12.

Рисунок 29 – Нахождение амплитуды для новой таблицы

Рисунок 30 – Первая гармоника для новой таблицы

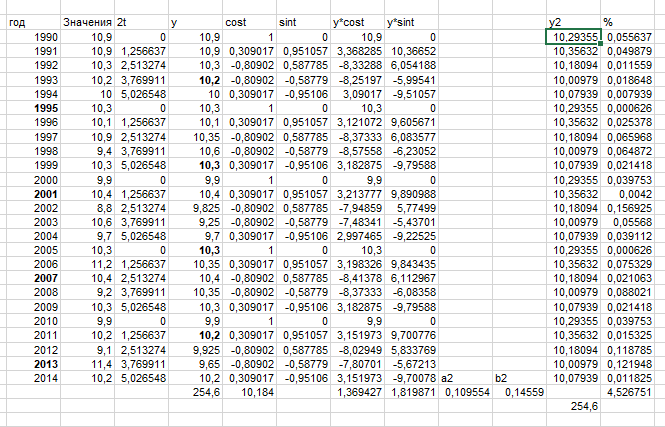
Рисунок 31 – Вторая гармоника для новой таблицы

% погрешности в 1 и 2 гармонике (2,68% и 4,53) после исключения аномалий , что значительно ниже 5%, и полученных в 1 измерении 4.596%.,

Вывод:

Самая первая гармоника оказалась приемлемым результатом, но максимально приближённым к ожидаемому результату, соответствует 1 гармоника после исключения аномалий по методу Фурье.

Уравнение: ,

Где , , ,

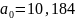При этой гармонике средняя ошибка аппроксимации E = 2,684378 %, что свидетельствует о плохом подборе модели (уравнения) к исходным данным.

Метод Фурье дал более точные результаты. И удалось приблизиться к значению ошибки значительно меньше 5%, что говорит о том, что итоговая выборка значений после исключения аномалий достаточна точна.

В результате задания был выделен тренд временного ряда и проведен его анализ, также было выполнено приближение к исходному ряду путём задания гармонического уравнения