МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

Кафедра проблемно-ориентированных вычислительных комплексов

ОЦЕНКА

ПРЕПОДАВАТЕЛЬ

доцент _________________ А.В. Аграновский

подпись, дата

КОНТРОЛЬНАЯ РАБОТА

Использование линейных алгоритмов обработки данных

по дисциплине «Технологии программирования»

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. Z9411 __________________ А.С. Чурилов

подпись, дата

Студенческий билет № 2019/3684

Санкт-Петербург 2021г.

Оглавление

1. Постановка задачи 3

2. Математическая модель 3

3. Описание разработанной программы 4

4. Описание тестового набора 6

5. Примеры работы программы 8

Вывод 9

Приложение 1. Листинг программного кода 10

1. Постановка задачи

Формулировка задания (задание №19): даны коэффициенты квадратного уравнения a, b, c; рассчитайте сумму и произведение корней по формулам Виета.

Входными параметрами являются три отличных от нуля, вещественных числа, которые в программе выступают в качестве коэффициентов квадратного уравнения.

Конечная цель программы – вычисление суммы и произведения корней квадратного уравнения и вывод их на экран.

2. Математическая модель

Сумма корней приведенного квадратного трехчлена 

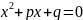
равна его второму коэффициенту p с противоположным знаком, а произведение - свободному члену q, то есть

В случае неприведенного квадратного уравнения 

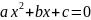
формулы Виета имеют вид:

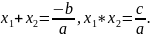
Значимость теоремы Виета заключается в том, что, не зная корней квадратного трехчлена, легко можно вычислить их сумму и произведение, то есть простейшие симметричные многочлены от двух переменных x₁+x₂ и x₁*x₂. Теорема Виета позволяет угадывать целые корни квадратного трехчлена.

3. Описание разработанной программы

В качестве входных параметров имеем три характеристики, равные коэффициентам квадратного уравнения (см. табл. 1).

Таблица 1 – Перечень входных параметров
Имя переменной	Тип переменной	Описание
a	float	Коэффициент при х2
b	float	Коэффициент при х
c	float	Коэффициент при х=0

Все три переменные должны являться вещественными числами, неравными 0.

В таблице 2 приведен перечень выходных характеристик. Таковыми являются сумма и произведение корней уравнения, вычисляемые по специальным формулам, описанным в разделе «Математическая модель».

Таблица 2 – Перечень выходных параметров
Имя переменной	Тип переменной	Описание
sum_xx	float	Сумма корней квадратного уравнения
proiz_xx	float	Произведение корней квадратного уравнения

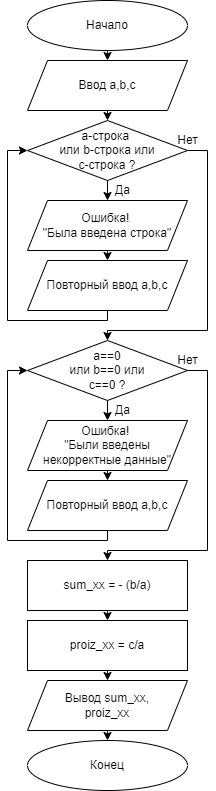
Разработанный для данной задачи алгоритм содержит разветвленные и циклические структуры (см. рис. 1).

Рисунок 1 – Блок-схема алгоритма

Вся программа состоит из трёх функций. Первая функция is_number(inp) даёт возможность проверить, содержит ли полученный параметр сторонние символы, отличные от цифр. Во второй функции LAB1_VAR_19(a, b, c) после осуществления проверок выполняется нахождение суммы и произведения корней заданного квадратного уравнения. В третьей функции TEST_LAB1_VAR_19() прописан автоматический тестовый сценарий, позволяющий проанализировать поведение программы при граничных условиях и различных форматах входных и выходных данных.

Листинг программного кода приведен в Приложении 1.

4. Описание тестового набора

Изучим набор тестовых случаев (см. табл. 3).

Таблица 3 –Тестовый набор
Описание тестового случая	Входные данные	Ожидаемый результат	Результат теста
Переменная а содержит буквенные символы	a = ”test”; b = 4; c = 2	Ошибка. «Была введена строка!»	Пройден
Переменная b содержит буквенные символы	a = 1; b = ”test”; c = 2	Ошибка. «Была введена строка!»	Пройден
Переменная c содержит буквенные символы	a = 1; b = 4; c = ”test”	Ошибка. «Была введена строка!»	Пройден
Переменная a равна 0	a = 0; b = 4; c = 2	Ошибка. «Были введены некорректные данные!»	Пройден
Переменная b равна 0	a = 1; b = 0; c = 2	Ошибка. «Были введены некорректные данные!»	Пройден
Переменная c равна 0	a = 1; b = 4; c = 0	Ошибка. «Были введены некорректные данные!»	Пройден
Введены коэффициенты приведенного квадратного уравнения, все коэффициенты положительные	a = 1; b = 4; c = 2	sum_xx = -4 proiz_xx = 2	Пройден
Введены коэффициенты неприведенного квадратного уравнения, коэффициенты имеют разные знаки	a = 3; b = -6; c = 9	sum_xx = 2 proiz_xx = 3	Пройден

Ожидаемые результаты вычислялись вручную согласно описанной математической модели.

5. Примеры работы программы

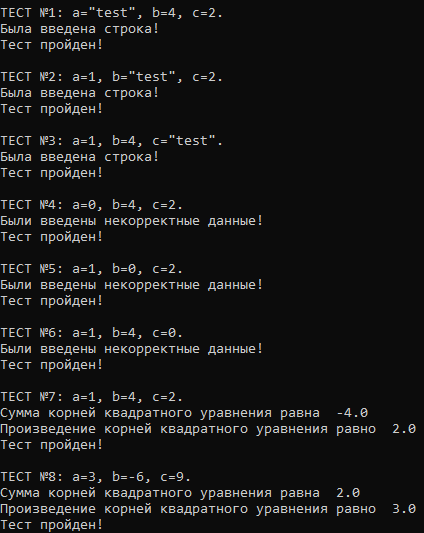
Далее представлен пример работы написанной программы с подобранными тестовыми значениями (см. рис. 2).

Рисунок 2 – Пример работы программы

Вывод

В ходе выполнения лабораторной работы была реализована программа расчета суммы и произведения корней квадратного уравнения по формулам Виета. Были получены практические навыки написания структурно продуманных программ на языке программирования Python3.

Было проведено тестирование разработанной программы. Во всех случаях полученный результат совпал с ожидаемым, что позволяет сделать вывод о корректной работе созданной программы.

Приложение 1. Листинг программного кода

import math #модуль для мат. операций

#функция проверки введенного числа на сторонние символы

def is_number(inp):

try:

float(inp)

return True

except ValueError:

return False

#основная функция

def LAB1_VAR_19(a,b,c):

if is_number(a)==False or is_number(b)==False or is_number(c)==False:

print("Была введена строка!")

return('Error!')

elif a==0 or b==0 or c==0:

print("Были введены некорректные данные!")

return('Error!')

else:

sum_xx=-(b/a) #сумма корней по Виету

proiz_xx=c/a #произведение корней по Виету

return sum_xx, proiz_xx

#автоматический тестовый сценарий

def TEST_LAB1_VAR_19():

err='Error!'

print('ТЕСТ №1: a="test", b=4, c=2.')

a='test'

b=4

c=2

ans=LAB1_VAR_19(a, b, c)

if ans==err:

print('Тест пройден!')

else:

print('Тест не пройден!')

print('\nТЕСТ №2: a=1, b="test", c=2.')

a=1

b='test'

c=2

ans=LAB1_VAR_19(a, b, c)

if ans==err:

print('Тест пройден!')

else:

print('Тест не пройден!')

print('\nТЕСТ №3: a=1, b=4, c="test".')

a=1

b=4

c='test'

ans=LAB1_VAR_19(a, b, c)

if ans==err:

print('Тест пройден!')

else:

print('Тест не пройден!')

print('\nТЕСТ №4: a=0, b=4, c=2.')

a=0

b=4

c=2

ans=LAB1_VAR_19(a, b, c)

if ans==err:

print('Тест пройден!')

else:

print('Тест не пройден!')

print('\nТЕСТ №5: a=1, b=0, c=2.')

a=1

b=0

c=2

ans=LAB1_VAR_19(a, b, c)

if ans==err:

print('Тест пройден!')

else:

print('Тест не пройден!')

print('\nТЕСТ №6: a=1, b=4, c=0.')

a=1

b=4

c=0

ans=LAB1_VAR_19(a, b, c)

if ans==err:

print('Тест пройден!')

else:

print('Тест не пройден!')

print('\nТЕСТ №7: a=1, b=4, c=2.')

a=1

b=4

c=2

sum_xx, proiz_xx=LAB1_VAR_19(a, b, c)

print("Сумма корней квадратного уравнения равна ", sum_xx)

print("Произведение корней квадратного уравнения равно ", proiz_xx)

if sum_xx==-4 and proiz_xx==2:

print('Тест пройден!')

else:

print('Тест не пройден!')

print('\nТЕСТ №8: a=3, b=-6, c=9.')

a=3

b=-6

c=9

sum_xx, proiz_xx=LAB1_VAR_19(a, b, c)

print("Сумма корней квадратного уравнения равна ", sum_xx)

print("Произведение корней квадратного уравнения равно ", proiz_xx)

if sum_xx==2 and proiz_xx==3:

print('Тест пройден!')

else:

print('Тест не пройден!')

TEST_LAB1_VAR_19() #вызов тестовой функции