0017

1. Введение

В настоящее время интерес к разработкам мощных многомодовых лазерных диодов на основе гетероструктур InGaAs/AlGaAs/GaAs, обеспечивающих генерацию импульсов с пиковой мощностью десятки и сотни ватт длительностью десятки наносекунд в спектральном диапазоне 900 – 1060 нм, обусловлен, в том числе, активным развитием таких приложений, как лазерная дально­ метрия и связь в свободном пространстве. За последнее десятилетие опубликован ряд экспериментальных и теоретических работ, посвящённых исследованию излучательных характеристик таких лазеров [1 – 8]. Экспери­ ментальные исследования продемонстрировали возможность работы полупроводниковых лазеров при накачке импульсами тока амплитудой от нескольких десятков до сотен ампер, при этом ограничения их работы были связаны с насыщением излучаемой мощности. Для интерпретации полученных результатов и оптимизации лазерной гетероструктуры был разработан и проанализирован ряд моделей [1 – 13]. Уже в простейших одномерных моделях, учитывающих транспорт носителей заряда в гетероструктуре, был определен ряд эффектов, ответственных за усиление действия различных механизмов потерь при высоких токах накачки: накопление носителей заряда в волноводных слоях лазерной гетероструктуры [3, 6, 7], двухфотонное поглощение излучения при высоких плотностях мощности в области волновода [4, 7, 9], рекомбинационныепотеривволноводныхслоях[2, 7].Следующим шагом в развитии моделей был учет особенностей неравномерного распределения плотности фотонов и материального усиления вдоль оси резонатора. Здесь можно от-

С.О.Слипченко, О.С.Соболева, В.С.Головин, Н.А.Пихтин. Физи­ ко-технический институт им. А.Ф.Иоффе РАН, Россия, 194021 С.-

Петербург­ , Политехническая ул., 26; e-mail: Serghpl@mail.ioffe.ru

Поступила в редакцию 9 августа 2022 г.

метить как простейшие 1D модели, в которых не учи­ тывался транспорт носителей в слоях гетероструктуры [1, 5, 10, 11], так и 2D модели, в которых учитывался как транспорт носителей. так и неравномерность распределения плотности фотонов [2, 6, 7, 12, 13].

В результате теоретически [2, 12] и экспериментально [12, 14] было установлено, что неоднородное распределение фотонов вдоль резонатора (продольное пространственное выжигание дырок, LSHB) и, как следствие, неоднородное распределение материального усиления и концентрации носителей в активной области приводят к неоднородности в распределении плотности тока вдоль резонатора, которую можно определить как продольное пространственное выжигание тока, LSCB. Эффект LSCB принципиально не выявляется в 1D моделях, что ведет к недооценке потерь в области высоких токов накачки [2]. Кроме того, на величину этого эффекта и его вклад в насыщение ватт-амперной характеристики (ВтАХ) оказывают влияние такие параметры кристалла полупроводниковых лазеров, как длина резонатора и неравенство коэффициентов отражения зеркал резонатора.

Все это говорит о том, что для получения мощных импульсных полупроводниковых лазеров необходим не только анализ свойств выбранного дизайна гетероструктуры, но и оптимизация параметров лазерных кристаллов – длины и коэффициентов отражения зеркал резонатора. В рамках настоящей работы на основе разработанной 2D модели мощных полупроводниковых лазеров проведен анализ механизмов насыщения ВтАХ в области высоких токов накачки и влияния параметров лазерного кристалла на выбор рабочей точки, которая определяется как максимальная мощность, достигаемая при заданной амплитуде импульсов тока.

2. Описание модели

Для моделирования ВтАХ лазерных диодов использовалась статическая 2D модель, учитывающая транспорт

носителей заряда в слоях гетероструктуры и распределение фотонов вдоль резонатора. Кроме того, с целью наглядной демонстрации вклада эффектов LSHB и LSCB в насыщение ВтАХ проведен сравнительный анализ полученных результатов с результатами расчетов, полученных в 1D модели, учитывающей только транспорт носителей в слоях гетероструктуры. Рассмотренный в работе импульсный режим накачки соответствовал длительностям, при которых, с одной стороны, тепловым разогревом лазера можно пренебречь, а с другой стороны, режим работы лазера можно рассматривать как стационарный и пренебречь переходными процессами при включении генерации. Данные приближения являются важными, поскольку неоднородный тепловой разогрев вдоль оси резонатора при работе, например, в непрерывном режиме может оказывать влияние на эффекты LSHB и LSCB [12, 14].

В 1D модели рассматривался дрейф-диффузионный транспорт носителей по оси x, перпендикулярной слоям гетероструктуры, c использованием уравнений Пуассона и непрерывности для электронов и дырок:

где n, p – концентрации свободных электронов и дырок соответственно; y – электростатический потенциал; ND+ ,

N-A – концентрация ионизированных примесей доноров

иакцепторов; R – скорость рекомбинации (излучательная, Шокли – Рида – Холла, Оже и стимулированная); q – элементарный заряд; e – диэлектрическая проницаемость;

e0 – диэлектрическая постоянная; mn, mp – коэффициенты подвижности электронов и дырок соответственно; Dn, Dp

– коэффициенты диффузии электронов и дырок, которые рассчитывались через коэффициенты подвижности по соотношениям Эйнштейна.

Рекомбинация Шокли – Рида – Холла

(где n1 = n0 [(1 – ft0)/ft0], p1 = p0 [ ft0 /(1 – ft0)], ft0 = {1 + exp[(Et –

EF)/kT]}–1); излучательная рекомбинация

оже-рекомбинация

Здесь n0 , p0 – равновесные концентрации носителей; ft0 – доля заполненных ловушек захвата, расположенных на уровне Et; EF – энергетический уровень Ферми; T – темпе-

ратура, равная 300 K; k – постоянная Больцмана; B – коэффициент излучательной рекомбинации; Cn, p – коэффициенты оже-рекомбинации; tn, p – коэффициенты модели рекомбинации Шокли – Рида – Холла, или времена жизни носителей.

В 1D модели лазерная генерация рассчитывалась на основе сосредоточенного скоростного уравнения для концентрации фотонов S:

где ug – групповая скорость фотонов в резонаторе; g – модальное усиление; aint – внутренние оптические потери; am = [1/(2L)]ln[1/(RARRHR)] – потери на выход излучения;

L – длина резонатора; RAR, HR – коэффициенты отражения его зеркал; bsp – коэффициент спонтанного излуче-

ния, т. е. доля спонтанного излучения, входящего в лазерную моду; Rrad – темп излучательной рекомбинации.

Итак, в 1D модели концентрация фотонов рассчитывалась из сосредоточенной модели скоростных уравнений (5), а концентрация носителей и потенциал – на основе дрейф-диффузионного приближения (1) – (4). Одно­ мерность данной модели понимается в том смысле, что транспорт носителей рассматривается перпендикулярно оси роста кристалла, а лазерная генерация – в сосредоточенной модели.

При переходе к 2D приближению добавляоась ось y, направленная вдоль оси резонатора, причем вдоль нее рассматривалась только лазерная модель, а транспорт рассчитывался, как и в 1D модели, только по оси x. Лазерный резонатор (вдоль оси y) разбивался на m сегментов, причем номер сегмента i = 1 – 30, в каждом из которых рассчитывались уравнения дрейф-диффузии. Со­ седние­ точки по координате связывались между собой через концентрацию фотонов, продольный транспорт свободных носителей заряда не учитывался. Значения S+ и S– из выражений (6а) и (6б), обозначающие концентра­ ции фотонов, движущихся вдоль оси резонатора в противоположных направлениях, задавались на границах сегментов, при этом каждому i-му сегменту соответствует концентрация фотонов Si = S+i + S–i,

где aFCA – внутренние оптические потери на свободных носителях; S+ и S– – интегральные концентрации фотонов в каждом сегменте (интеграл по оси x), поэтому выражаются в см–2. Более подробно данный подход описан в [1].

Пиковая оптическая мощность для выходного зеркала в 1D модели выражалась следующей формулой:

где w – ширина полоскового контакта; hc/l – энергия единичного фотона; h – постоянная Планка; c – скорость света; l – длина волны излучения.

Для описания усиления в активной области лазерного диода (G(n, p)) использовалось выражение G(n, p) = G0 ´ ln(min(n, p)/ntr, где G0 и ntr – параметры модели усиления. В 2D модели для определения мощности со стороны вы-

ходного зеркала с коэффициентом отражения RAR использовалось выражение (8) при условии, что антиотражающее (AR) зеркало расположено в точке y = 0:

где S–|y = 0 – концентрация фотонов у выходного зеркала. Поскольку настоящая работа является продолжением цикла расчетных работ [1, 2], то в проведенном анализе параметры конструкции лазерной гетероструктуры оставались неизменными: высоколегированные N- и P-эмит­ теры Al0.3Ga0.7As толщиной 0.2 и 0.1 мкм соответственно, нелегированный волновод Al0.1Ga0.9As толщиной 1.7 мкм и активная область InGaAs толщиной 9 нм (излучает на длине волны 1060 нм), окруженная GaAs-спейсерами толщиной 10 нм. Расстояние между активной областью и P-эмиттером составляло 0.65 мкм. Используемые в модели параметры герероструктуры и лазерных диодов при-

ведены ниже.

Рис.1.  Ватт-амперные характеристики лазерных диодов с различными длинами резонатора L при RAR = 1 %, рассчитанные по 2D (сплошные кривые) и 1D (штриховые кривые) моделям.

енты отражения выходного зеркала RAR = 0.1 %, 1 %, 3 %, длины резонаторов L = 1.5 – 11 мм. В качестве примера на рис.1 показаны типичные ВтАХ для RAR = 1 % и L = 1– 11 мм. Если не рассматривать поведение ВтАХ в области малых токов накачки, то традиционно характер ВтАХ можно описать, используя такие параметры, как пороговый ток и внешняя дифференциальная эффективность. Из рис.1 видно, что увеличение тока накачки сопровождается снижением локального наклона ВтАХ (для выбранного тока накачки его можно определить как отношение приращения мощности к приращению тока) и, в конечном итоге, полным насыщением роста выходной оптической мощности. С увеличением длины резонатора полное насыщение выходной оптической мощности наблюдается при более высоких токах накачки. Наиболее выраженное насыщение ВтАХ проявляется в 2D модели, тогда как, согласно расчетам в 1D модели, эффекты насыщения наблюдаются только для коротких резонаторов. В рассмотренном примере (рис.1) максимальная длина резонатора L, при которой имеет место полное насыщение ВтАХ, составляет ~2 мм для 2D модели и ~1 мм для 1D модели, при этом уменьшение RAR смещает данные значения в область бóльших длин резонатора (рис.2). Поскольку для большинства практических случаев мак-

3. Результаты расчетов ВтАХ лазерных диодов

На первом этапе были сделаны расчеты ВтАХ лазерных диодов, полученные в 1D и 2D моделях. Расчеты проводились для следующего набора параметров: коэффици-

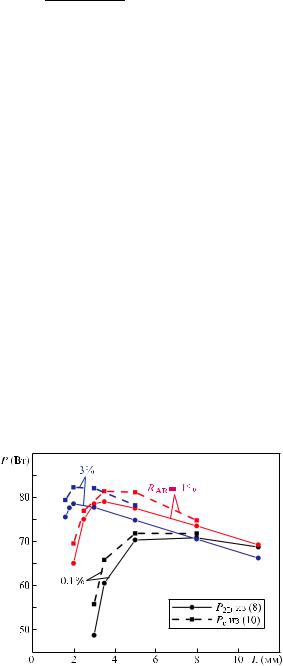
Рис.2.  Зависимости пиковой оптической мощности P от длины резонатора L для различных значений коэффициента отражения выходного зеркала RAR, рассчитанные по 2D (сплошные кривые, кружки) и 1D (штриховые кривые, квадраты) моделям для пикового тока I = 150 А.

симальный пиковый ток источника накачки полупровод­ никовых лазеров является фиксированным, то в рамках данных расчетов для анализа была выбрана амплитуда тока накачки 150 А и для нее построены зависимости выходной оптической мощности от L для различных значений RAR (рис.2). Видно, что для заданного RAR существует оптимальная длина резонатора Lopt, при которой достигается максимальная мощность для фиксированной амплитуды тока накачки (150 А). Также видно, что при снижении RAR оптимальными для достижения максимальной мощности являются более длинные резонаторы. Однако характеры зависимостей максимальной оптической мощности от длины резонатора или коэффициента отражения выходного зеркала для 1D и 2D моделей заметно различаются.

Расчет ВтАХ по 1D модели подтверждает вывод, который можно сделать исходя из общих соображений на основании следующего соотношения [15]:

где n – частота единичного фотона; q – единичный заряд; hi (I ) = (I – Iloss)/I – внутренняя квантовая эффективность; hd = am /(am + ai) – дифференциальная эффективность; am – потери, связанные с выходом излучения из резонатора; ai – внутренние оптические потери; Iloss – ток рекомбинационных потерь; I – ток накачки. Можно сказать, что выходная мощность P определяется амплитудой­ тока накачки I, при этом рост оптических потерь ai в области высоких токов накачки для лазеров с различной длиной резонатора связан, в том числе, с накоплением свободных носителей в слоях гетероструктуры за счет роста плотности тока накачки. Поэтому, увеличивая длину резонатора, можно обеспечить условия, при ко­торых, сохраняя амплитуду тока накачки, можно снизить плотность тока, а значит, снизить воздействие увеличи­ вающихся­ внутренних оптических потерь. Однако с рос­том L одним из основных факторов, ограничивающих выходную мощность, становятся низкие потери на выход am, которые приближаются к внутренним оптическим потерям ai. В этом случае для повышения эффективности и мощности, казалось бы, можно использовать подход, основанный на повышении am за счет снижения коэффициентов­ RAR для лазеров с большими длинами резонаторов­ . Дейст­ вительно, для области высоких токов накачки и выбранных диапазонах параметров RAR = 0.1 % – 3 % и L = 1 – 11 мм расчеты по 1D модели де­монстрируют, что максимальная мощность излучения достигается при минимальном RAR (рис.2, штриховая кривая для RAR = 0.1 %). Расчет по 2D модели показывает, что при снижении коэффициента RAR часть законо­мерностей сохраняется: максимальная оптическая мощность излучается лазерными диодами с большей длиной резонатора. Однако наибольшая мощность достигается при RAR = 1 % – 3 %, а дальнейшее снижение RAR до 0.1 % приводит к падению мощности (рис.2, сплошные кривые). Таким образом, существует набор оптимальных значений параметров кри-

сталла лазерного диода Lopt и RAR opt, при которых обеспечивается достижение­ максимальной выходной опти-

ческой мощности в области высоких токов накачки, а изменение L и RAR относительно оптимальных значений, в частности уменьшение­ RAR и увеличение L, приводит к падению излучаемой­ мощности.

4. Анализ потерь, приводящих к насыщению ВтАХ лазерных диодов

Проанализируем влияние различных механизмов потерь на насыщение ВтАХ, следствием которого является формирование области оптимальных значений параметров резонатора лазера. Как показано в работе [2], для анализа потерь, приводящих к насыщению ВтАХ, можно использовать подход, основанный на расчете выходной оптической мощности по формуле (9), в которой значе-

ния параметров am  2D, ai  2D, Iloss  2D рассчитываются по данным из 2D модели:

q am 2D + ai 2D

где Pc – мощность, рассчитанная из формулы (9). Данное соотношение позволяет просто оценить пар-

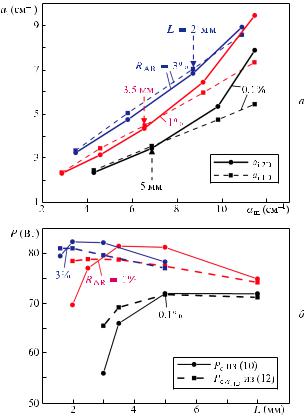
циальные вклады существующих механизмов оптических потерь. Для демонстрации корректности использования предлагаемого подхода мы сравнили значения пиковых мощностей, рассчитанных с помощью соотношения (10) (рис.3, квадраты), и значения, полученные при полном расчете в рамках 2D модели (рис.3, кружки). Видно, что характеры зависимостей P(L) совпадают, а различие значений P, полученных при полном расчете в 2D модели и по формуле (10), не превышает 5 %. Таким образом, расчет выходной оптической мощности с использованием простого аналитического соотношения (10) и значений параметров, полученных в 2D модели, позволяет оценить парциальный вклад каждого механизма потерь в насыщение оптической мощности для различных параметров резонатора. Для наглядной демонстрации парциального вклада каждого механизма потерь проводились расчеты пиковой мощности по соотношению (10), когда все пара-

метры, am  2D, ai  2D и Iloss  2D, определялись из расчетов, проведенных в 2D модели, а также когда использовалось

значение одного из анализируемых параметров, рассчи-

танное в 1D модели (am  1D, ai  1D или Iloss  1D).

Рассмотрим влияние внутренних оптических потерь на насыщение ВтАХ с использованием выражения (10). Для этого был проведен расчет модальных внутренних оптических потерь

Рис.3.  Зависимости пиковой оптической мощности P от длины резонатора L для различных значений коэффициента отражения выходного зеркала RAR, полученные по 2D модели (сплошные кривые, кружки) и рассчитанные для пикового тока I =150 А по формуле (10) (штриховые кривые, квадраты).

i = 0

где aFCA, MOD – суммарные (интегральные) модальные внутренние оптические потери; aFCA  i – внутренние оптические потери в i-м сегменте;

i = m Gi = Si / /Si

i= 0

–фактор оптического ограничения вдоль оси резонатора для i -го сегмента. Данное соотношение учитывает парциальные вклады в оптические потери различных локальных i-х областей, составляющих резонатор в 2D модели,

для которых факторы оптического ограничения Gi рассчитывались как отношение числа фотонов в i-м сегменте Si к общему числу фотонов в резонаторе, состоящем из m

сегментов. При этом оптические потери aFCA  i в i-м сегменте резонатора определяются распределением поля

моды поперечного волновода и концентрациями свободных носителей заряда в слоях гетероструктуры i-го сегмента. Именно неоднородное распределение тока вдоль резонатора и определяет различие значений aFCA  i.

На рис.4,а приведены зависимости суммарных модальных внутренних оптических потерь ai  2D от потерь на выход излучения am = (1/2L)ln(1/RARRHR) для 2D модели и те же зависимости, полученные в 1D приближении. На зависимостях ai  2D(am) для представленных значений RAR можно выделить три участка. Первый характерен для условно малых длин резонатора (больших am), где расчеты по 1D модели дают значения внутренних оптических потерь, заниженные относительно ai  2D, полученных в 2D модели. Данное обстоятельство связано с формированием локальных областей резонатора с высокими оптическими потерями у граней c высоким коэффициентом отражения RHR, где плотность тока высока, что не учиты­ вает 1D модель. Второй участок, соответствующий бóльшим длинам резонатора, характеризуется переоценкой значений потерь, рассчитанных в 1D модели, относи-

тельно значений ai  2D. При этом чем больше RAR, тем меньше длина резонатора, при которой наблюдается пе-

реход от первого ко второму участку (рис.4,а). Различие поведения внутренних оптических потерь, полученных в 1D и 2D моделях для первого и второго участков, объясняется локализацией областей с высокой концентрацией свободных носителей в слоях гетероструктуры и высокими внутренними оптическими потерями у граней c большим коэффициентом отражения RHR,а также локализацией области с высоким фактором оптического ограничения моды вдоль резонатора у выходного зеркала с RAR, где концентрации носителей и оптические потери ниже, чем рассчитанные в 1D модели [2]. Таким образом, в 2D модели модальные внутренние оптические потери существенным образом зависят от интеграла перекрытия данных областей в резонаторе, на значение которого также влияет ток накачки, что не учитывается в 1D модели. Дальнейшее увеличение длины резонатора (уменьшение am) приводит к тому, что внутренние оптические потери, полученные в 1D и 2D моделях, практически сравниваются, что соответствует третьему участку.

Для оценки парциального вклада внутренних оптических потерь, полученных в 2D модели, был проведен расчет пиковой оптической мощности по формуле (10), в которой использовалось значение внутренних оптических потерь, полученной по 1D модели,

Рис.4.  Зависимости модальных внутренних оптических потерь ai от потерь на выход излучения am = [1/(2L)]ln(1/RARRHR) для разных длин резонатора, полученные в 2D (сплошные кривые, кружки) и 1D (штриховые кривые, квадраты) моделях для пикового тока I = 150 А, оптические потери ai  2D рассчитывались в соответствии с выражением (11) (а), а также зависимости пиковой оптической мощности P от длины резонатора L, рассчитанные для пикового тока I = 150 А по формулам (10) (сплошные кривые) и (12) (штриховые кривые) (б).

Результаты расчетов по формулам (10) и (12), приведенные на рис.4,б, показывают, что для длинных резонаторов, независимо от коэффициента отражения выходного зеркала RAR, изменение внутренних оптических потерь за счет эффектов LSHB и LSCB существенно не влияет на оптическую мощность. Однако для коротких резонаторов недооценка внутренних оптических потерь в 1D модели приводит к существенной переоценке излучаемой мощности, что обусловлено пренебрежением эффектами LSHB и LSCB, действие которых еще более усиливается при снижении RAR.

Следующий механизм потерь связан с рекомбинационным током Iloss. Для 2D модели ток рекомбинационных потерь вдоль оси резонатора y определялся на основе следующего соотношения:

где JSRH, JRAD и JAug – плотности тока рекомбинации Шокли – Рида – Холла, излучательной рекомбинации и оже-рекомбинации соответственно. При этом каждая из компонент рекомбинационных потерь является интег­

ральной характеристикой для всех слоев гетерострук­ туры.

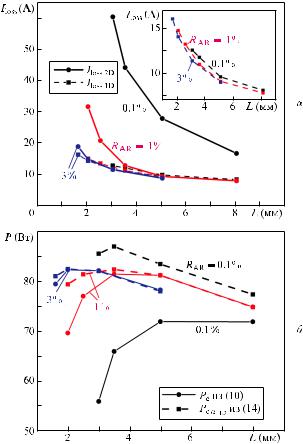
На рис.5,а приведены зависимости суммарных реком-

бинационных токов, рассчитанных по 1D (Iloss  1D) и 2D (Iloss  2D) моделям для различных значений RAR. Видно, что при RAR = 3 % и в диапазоне длин резонаторов 1.5 – 8 мм

токи рекомбинационных потерь, рассчитанные в 1D и 2D моделях, различаются незначительно. Уменьшение RAR приводит к занижению токов рекомбинационных потерь, рассчитанных в 1D модели. При этом разница между рас-

считанными значениями Iloss  2D и Iloss  1D с уменьшением длины резонатора растет. Как было показано в [2], основ-

ной источник рекомбинационных потерь расположен у грани c высоким коэффициентом отражения RHR и определяется неоднородным распределением фотонов и оптических потерь вдоль резонатора. Это обусловлено тем, что низкая концентрация фотонов у граней c RHR приводит к необходимости достижения большего материального усиления и, следовательно, более высоких концентраций носителей в активной области, что в свою очередь приводит к повышению плотности тока в данной области и к накоплению носителей в слоях гетероструктуры. Данный механизм запускает положительную обратную связь, которая усиливается при уменьшении длины резонатора за счет как роста пороговой концентрации носи-

Рис.5.  Зависимости рекомбинационных токов Iloss от длины резонатора L, полученные в 2D (сплошные кривые, кружки) и 1D (штриховые кривые, квадраты) моделях для пикового тока I = 150 А, в 2D модели рекомбинационные токи рассчитывались в соответствии с выражением (13) (а), а также зависимости пиковой оптической мощности P от длины резонатора L, рассчитанные для пикового тока I = 150 А по формулам (10) (сплошные кривые) и (14) ( штриховые кривые) (б).

телей при увеличении потерь на выход излучения, так и насыщения усиления в активной области с ростом пороговой концентрации.

Для оценки парциального вклада рекомбинационных потерь, полученных в 2D модели, был проведен расчет пиковой оптической мощности по формуле (10), в которой использовалось значение рекомбинационных потерь, полученное в 1D модели:

Мощности, рассчитанные из соотношений (10) и (14) для различных параметров резонатора и учитывающие токи рекомбинационных потерь, полученные в 1D и 2D моделях, показаны на рис.5,б. Видно, что недооценка тока

Iloss  1D приводит к завышению расчетной мощности для лазеров с малой длиной резонатора. Однако данный эф-

фект нивелируется при увеличении RAR и свидетельствует о том, что эффекты LSHB и LSCB не вносят существенного вклада в ток рекомбинационных потерь и, соответственно, в выходную мощность. Однако для лазеров с малым значением RAR (в нашем случае RAR = 0.1 %) вклад эффектов LSHB и LSCB в величину тока рекомбинаци­ онных потерь и, как следствие, в выходную мощность является существенным для всего диапазона длин резона­ торов.

Еще одним источником оптических потерь являются потери am, связанные с выходом излучения из резонатора. В отличие от других, данный вид оптических потерь особенно важен для мощных полупроводниковых лазеров, поскольку от него существенно зависит величина выходной оптический мощности. В общем случае эти потери определяются как отношение энергии, запасенной в резонаторе, к энергии, вышедшей (в нашем случае) через грань с малым коэффициентом отражения RAR. В отличие от 1D модели, изменение запасенной энергии или суммарного числа фотонов в резонаторе в 2D модели может приводить к изменению потерь на выход излучения. В то время как в 1D приближении потери на выход остаются неизменными и выражаются простым соотношением am = (1/2L)ln(1/RARRHR), для 2D модели мы можем ввести эффективные потери на выход излучения, выраженные через концентрации фотонов, которые пропорциональны энергиям, запасенным в резонаторе и выходящим из резонатора:

i = 0

Рассчитанные для 1D и 2D моделей зависимости

am  1D (L) и am  2D (L), полученные для различных RAR, показаны на рис.6,а. Видно, что во всех исследуемых диа­

пазонах длин резонаторов и значений RAR имеет место завышение потерь на выход излучения, рассчитанных в 1D модели, по сравнению с 2D моделью. При этом с увеличением RAR различие рассчитанных потерь умень­ шается.

Для оценки парциального вклада потерь на выход излучения, полученных в 2D модели, был проведен расчет пиковой оптической мощности по формуле (10), в которой использовалось значение потерь, полученное в 1D модели:

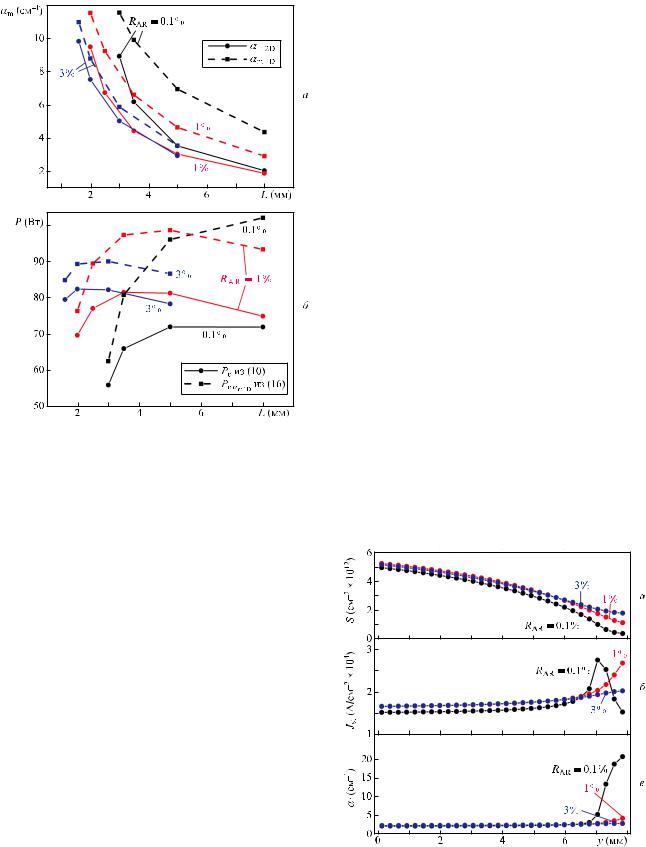
Рис.6.  Зависимости потерь на выход излучения am от длины резонатора L, полученные в 2D (сплошные кривые, кружки) и 1D (штриховые кривые, квадраты) моделях для пикового тока I = 150 А, эффективные потери на выход в 2D модели рассчитывались по формуле (15) (а), а также зависимости пиковой оптической мощности P от длины резонатора L, рассчитанные для пикового тока I = 150 А по формулам (10) (сплошные кривые) и (16) (штриховые кривые) (б).

ются в 1D модели, кроме того, эффекты LSHB и LSCB усиливают вклад этих потерь для резонаторов с низким коэффициентом RAR за счет насыщения усиления и роста пороговой концентрации в активной области. Однако при переходе в область длинных резонаторов определяющий вклад в снижение пиковой мощности дают потери, связанные с выходом излучения из резонатора (рис.6). Из выражения (15) для эффективных потерь на выход излучения, полученного для 2D модели, следует, что снижение am  2D связано с увеличением именно доли запасенной в резонаторе энергии относительно энергии, выведенной через выходное зеркало. Это значит, что может быть реализована такая ситуация, когда число фотонов у выходной грани снизится и, как следствие, снизится выходная мощность, при этом энергия, запасенная в резонаторе, также снизится, а отношение (15), определяющее потери на выход, останется неизменным.

Данная ситуация реализована для потерь на выход, рассчитанных в 2D модели для лазеров с длинными резонаторами (см. рис.6,а). Видно, что для L > 5 мм величины am  2D практически одинаковы при RAR = 0.1 % – 3 %. Следовательно, потери на выход излучения am  2D не дают прямого указания на физические причины изменения выходной оптический мощности. Как показывают расчеты распределений фотонов вдоль оси резонатора, при L = 8 мм и RAR = 0.1 % – 3 % число фотонов, запасенных в резонаторе, с увеличением RAR возрастает (рис.7,а). Однако это не приводит к падению выходной мощности, поскольку рост компенсируется большей эффективностью резонаторов с высокими значениями RAR с точки зрения внутренних оптических потерь и рекомбинационных потерь. В результате, даже при большем коэффициенте отражения RAR, излучаемая мощность оказывается выше за счет более высокого уровня мощности у выходного зеркала, несмотря на одинаковые значения am  2D и большее число фотонов, запасенных в резонаторе. Таким обра-

Влияние потерь на выход излучения на выходную оптическую мощность, рассчитанную по выражениям (10) и (16), показано на рис.6,б. Видно, что уменьшение длины резонатора снижает парциальный вклад эффектов LSHB и LSCB, связанных с потерями на выход независимо от RAR. Наиболее сильное влияние переоценки потерь на выход излучения на выходную оптическую мощность наблюдается в области длинных резонаторов. Так, если

при L = 8 мм и RAR = 0.1 % – 1 % в 2D модели имеем am  2D ~ 2 см–1, то для 1D модели am  1D = 5 см–1 при RAR = 0.1 %. В

результате рассчитанная пиковая мощность 1D модели составляет 102 Вт, тогда как в 2D модели – всего 72 Вт.

5. Заключение

Для обобщения полученных результатов будем считать, что короткие резонаторы имеют длину L < 3 мм, а длинные резонаторы – L > 5 мм; данное деление условно, переход между этими значениями является плавным. Установлено, что при малых длинах резонатора основной вклад в насыщение ВтАХ и снижение выходной мощности в области высоких токов накачки дают эффекты, связанные с ростом оптических и рекомбинационных потерь (см. рис.4,а и 5,а). Данные виды потерь недооценива-

Рис.7.  Распределения концентрации фотонов вдоль резонатора (для каждого сегмента по оси y приведено проинтегрированное по оси x значение в см­–2) (а), плотности тока стимулированной рекомбинации вдоль резонатора (Jst = J – Jloss) (б) и внутренних оптических потерь для различных значений коэффициента отражения выходного зеркала (в) при длине резонатора L = 8 мм и токе накачки

I = 150 А.

зом, в области длинных резонаторов снижение am  2D является косвенным признаком наличия более высоких потерь в резонаторе за счет эффектов LSHB и LSCB, при этом абсолютное количество накопленных в резонаторе фотонов не обязательно должно увеличиваться при снижении RAR. В рассмотренном случае для лазеров с длинными резонаторами (L > 5 мм) вклад интегральных внутренних оптических потерь от действия эффектов LSHB и LSCB несущественен (см. рис.4), поэтому основная причина уменьшения am  2D связана с суммарным рекомбина-

ционным током Iloss  2D и снижением полезной компоненты тока накачки Jst, отвечающей за стимулированную ре-

комбинацию (рис.7,б), а также с распределением внутренних оптических потерь aFCA i вдоль резонатора.

Механизм, приводящий к снижению оптический мощности в области высоких токов накачки для длинных резонаторов с низкими коэффициентами отражения выходного зеркала, реализуется следующим образом. Из-за асимметричного распределения фотонов в резонаторе со стороны грани ( y = 8 мм) с коэффициентом отражения RHR (рис.7,а) формируется локальная область с высокой плотностью тока (эффект LSCB), при этом плотность тока в ней тем больше, чем сильнее асимметрия коэффициентов отражения. Поскольку концентрация фотонов в данной области минимальна, то увеличение плотности тока, с одной стороны, приводит к увеличению тока стимулированной рекомбинации (рис.7,б) и внутренних оптических потерь (рис.7,в) в области резонатора со стороны грани с RHR и, с другой стороны, к перераспределению плотности тока – снижению локальных плотностей тока стимулированной рекомбинации в остальных частях резонатора (рис.7,б). Видно, что высокие локальные внутренние оптические потери при RAR = 0.1 % существенно снижают концентрацию фотонов в области резонатора со стороны грани с RHR, выполняющих функцию

«затравки» для S– | y = 0 в выражениях (6б) и (8), а локальный рост плотности тока рекомбинационных потерь не

позволяет получить требуемый ток стимулированной рекомбинации в оставшейся основной части резонатора. Важно отметить, что для длинных резонаторов интегральные модальные внутренние оптические потери ai  2D, полученные при расчете в 2D модели, не отличаются от

значений ai  1D, рассчитанных в 1D модели (рис.4,а), однако, как показывают полученные выше результаты, важ-

ную роль в насыщении выходной мощности играет распределение потерь вдоль резонатора, что невозможно показать, основываясь только на абсолютном значении оптических потерь. Таким образом, полноценный анализ

процессов, протекающих в мощных полупроводниковых лазерах, и оптимизация их параметров возможны только при учете пространственных эффектов, надежно регистрируемых в многомерных моделях, в которых учитываются как транспорт носителей в слоях гетероструктуры, так и неоднородности вдоль оси резонатора.

Немаловажным остается вопрос подавления эффектов LSHB и LSCB в мощных полупроводниковых лазерах с длинными резонаторами, поэтому в дальнейшем мы планируем провести исследования при изменении как параметров подвижности носителей, рекомбинации и усиления, так и дизайна гетероструктуры.

Работа выполнена за счет гранта Российского научного фонда (проект № 19-79-30072).

1.Головин В.С., Шашкин И.С., Слипченко С.О., Пихтин Н.А.,

Копьёв П.С. Квантовая электроника, 50, 147 (2020) [Quantum

Electron., 50, 147 (2020)].

2.Слипченко С.О., Головин В.С., Соболева О.С., Ламкин И.А.,

Пихтин Н.А. Квантовая электроника, 52, 343 (2022) [Quantum

Electron., 52, 343 (2022)].

3.Veselov D.A., Bobretsova Y.K., Leshko A.Y., Shamakhov V.V., Slipchenko S.O., Pikhtin N.A. J. Appl. Phys., 126, 213107 (2019).

4.Avrutin E.A., Ryvkin B.S. Semicond. Sci. Tech., 32, 015004 (2016).

5.Avrutin E.A., Ryvkin B.S. J. Appl. Phys., 125, 023108 (2019).

6.Wang X., Crump P., Wenzel H., Liero A., Hoffmann T., Pietrzak A., Schultz Ch.M., Klehr A., Ginolas A., Einfeldt S., Bugge F., Erbert G., Trånkle G. IEEE J. Quantum Electron., 46, 658 (2010).

7.Wenzel H., Crump P., Pietrzak A., Wang X., Erbert G., Trånkle G. New J. Phys., 12, 085007 (2010).

8.Piprek J. Opt. Quanum Electron., 51, 1 (2019).

9.Dogan M., Michael C.P., Zheng Y., Zhu L, Jacob J.H. Proc. HighPower Diode Laser Technology and Applications XII (SPIE, 2014, vol. 8965, p. 89650P).

10.Chen Z., Bao L., Bai J., Grimshaw M., Martinsen R., DeVito M., Haden J., Leisher P. Proc. Novel In-Plane Semiconductor Lasers XI

(SPIE, 2012, vol. 8277, p. 245).

11.Hao T., Song J., Leisher P.O. Proc. Semiconductor Lasers and Laser Dynamics VI (SPIE, 2014, vol. 9134, p. 155).

12.Arslan S., Swertfeger R.B., Fricke J., Ginolas A., Stölmacker C., Wenzel H., Crump P.A., Patra S.K., Deri R.J., Boisselle M.C., Pope D.L. Appl. Phys. Lett., 117, 203506 (2020).

13.Soboleva O.S., Zolotarev V.V., Golovin V.S., Slipchenko S.O., Pikhtin N.A. IEEE T. Electron Dev., 67, 4977 (2020).

14.Arslan S., Wenzel H., Fricke J., Thies A., Ginolas A., Stölmacker C., Maaßdorf A., Eppich B., Swertfeger R.B., Patra S.K., Deri R.J., Boiselle M.C., Pope D.L., Leisher P.O., Trånkle G., Crump P. Proc. Novel In-Plane Semiconductor Lasers XXI (SPIE, 2022, vol. 12021, p. 93).

15.Coldren L.A., Corzine S.W., Mashanovitch M.L. Diode Lasers and Photonic Integrated Circuits (NJ, Hoboken: John Wiley & Sons, 2012, p. 218)