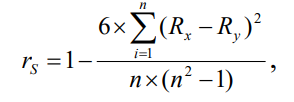УСР6

Управляемая самостоятельная работа №6

Корреляционный анализ

Выполнила: Ничипорук Анна, 23БХ-1

1. Степень и направление корреляционной зависимости.

Степень корреляционной зависимости измеряется коэффициентом корреляции, который может варьироваться от -1 до 1. Значение коэффициента корреляции указывает на силу и направление линейной зависимости между двумя переменными:

• Положительная корреляция: коэффициент корреляции положительный (от 0 до 1), когда значения одной переменной увеличиваются с увеличением значений другой переменной.

• Отрицательная корреляция: коэффициент корреляции отрицательный (от -1 до 0), когда значения одной переменной уменьшаются с увеличением значений другой переменной.

• Отсутствие корреляции: коэффициент корреляции близок к 0, когда между двумя переменными нет линейной зависимости.

Направление корреляции описывает, как одна переменная изменяется по отношению к другой.

2. Коэффициент корреляции Пирсона и оценка его статистической значимости.

Если признаки Y и X измерены в метрической шкале и имеют нормаль ное распределение, рассчитывают эмпирический коэффициент корреляции Пирсона r:

где n – общее число парных наблюдений, Sx, Sy – СКО признаков X и Y.

Статистическая значимость коэффициента корреляции Пирсона оценивается с помощью t-критерия Стьюдента. Нулевая гипотеза заключается в том, что коэффициент корреляции равен 0 (нет корреляции), а альтернативная гипотеза заключается в том, что он не равен 0 (существует корреляция).

3. Частная и множественная корреляции.

• Частная корреляция:Измеряет корреляцию между двумя переменными при контроле за влиянием одной или нескольких других переменных. Она показывает, насколько сильно две переменные связаны, когда влияние других переменных устранено.

• Множественная корреляция:Измеряет корреляцию между одной переменной и несколькими другими переменными, взятыми вместе. Она показывает, насколько сильно одна переменная связана с комбинацией других переменных. Коэффициент множественной корреляции (R) варьируется от 0 до 1 и представляет собой квадратный корень из коэффициента детерминации (R^2), который показывает процент вариации в одной переменной, объясняемый другими переменными.

4. Коэффициент ранговой корреляции Спирмена

Если варианты исследуемых признаков не распределяются по нормаль ному закону (или если распределение неизвестно), а также для признаков, измеренных в порядковой шкале, для определения связи между признаками используют непараметрические показатели. Наиболее широкое применение нашел коэффициент корреляции рангов, предложенный Спирменом.

Гипотезы:

Н0: в генеральной совокупности коэффициент корреляции Спирмена равен нулю, связь между изучаемыми признаками отсутствует.

Н1: в генеральной совокупности коэффициент корреляции Спирмена не равен нулю, есть связь между изучаемыми признаками.

Алгоритм проведения теста:

1. Сравниваемые признаки по отдельности ранжируют по возрастанию.

2. Каждой варианте каждого признака присваивается свой ранг (R) – порядковый номер того места, которое оно занимает в этом ряду. Одинако вым по величине вариантам присваивается один и тот же средний ранг.

3. Проверяют суммы рангов каждого признака, они должны получиться равными.

4. Находят разность между рангами для каждой пары вариант признаков X и Y.

5. Проверяют сумму разности рангов, она должна быть равной 0.

6. Рассчитывают квадрат разности между рангами для каждой пары ва риант.

7. Находят сумму квадратов разностей.

8. Рассчитывают коэффициент корреляции Спирмена по формуле:

9. Значимость коэффициента корреляции рангов оценивают с помощью коэффициента Стьюдента как для выборочного коэффициента корреляции.

Вывод: если фактически установленная величина tфакт – отношения вы борочного коэффициента корреляции к своей ошибке – больше tst. для чисел степеней свободы k = n – 2 на принятом уровне значимости β, нулевую гипо тезу отвергают. Иначе нулевую гипотезу отвергнуть нельзя.

Коэффициент рангов Спирмена может принимать значения от –1 до +1.