УСР3

Управляемая самостоятельная работа №3

Средние величины и показатели вариации количественных признаков

Выполнила: Ничпорук Анна, 23БХ-1

1. Коэффициенты асимметрии и эксцесса.

Для определения причин отклонения эмпирических распре делений от нормальной кривой рассчитывают показатели асимметрии As и эксцесса Ex (невзвешенные и взвешенные):

Статистические гипотезы:

Для коэффициента асимметрии:

Н0: в генеральной совокупности показатель асимметрии As равен нулю, данные распределяются по нормальному закону.

НА (или Н1): в генеральной совокупности показатель асимметрии As не равен нулю, данные не распределяются по нормальному закону.

Вывод: если величина tAs (отношение коэффициента асимметрии к своей ошибке) больше 3, нулевая гипотеза отвергается, принимается альтернативная, значит, исходные данные не распределяются по нормальному закону.

Для коэффициента эксцесса:

Н0: в генеральной совокупности показатель эксцесса Ex равен нулю, данные распределяются по нормальному закону.

НА (или Н1): в генеральной совокупности показатель эксцесса Ex не ра вен нулю, данные не распределяются по нормальному закону.

Вывод: если величина tEx (отношение коэффициента эксцесса к своей ошибке) больше 3, нулевая гипотеза отвергается, принимается альтернативная; значит, исходные данные не распределяются по нормальному закону.

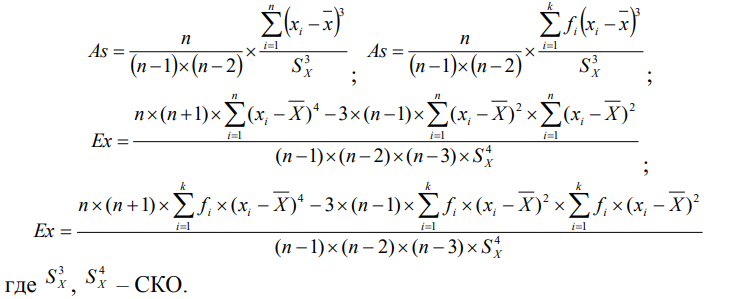
2. Средние величины: средняя арифметическая, взвешенная средняя, геометрическая средняя.

Средняя арифметическая невзвешенная величина рассчитывается по формуле:

где xi – индивидуальные значения признака;

i – порядковый номер варианты;

n – число наблюдений.

Средняя арифметическая взвешенная величина рассчитывается, если данные представлены сгруппированным вариационным рядом:

где xi – значения вариант признака;

fi – значения частот вариант вариационного ряда;

i – порядковый номер варианты, изменяющийся от 1 до k (количество частот).

Средняя геометрическая величина X g – более точная характеристика при определении средних прибавок, прироста численности популяции или изменения линейных размеров за определенный промежуток времени.

3. Меры разброса единиц совокупности: дисперсия и стандартное отклонение.

Средний квадрат отклонений вариант от средней величины называется смещенной дисперсией

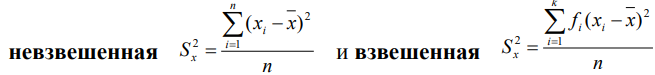
4. Индекс х у символа дисперсии обозначает, что этот показатель характе ризует варьирование числовых значений признака Х вокруг их средней вели чины. Чем менее однородна совокупность, тем большее значение будет иметь дисперсия.

   Среднее квадратическое отклонение – СКО (стандартное отклонение) – корень квадратный из дисперсии. Несмещенное СКО (для выборки):

   

   Смещенное СКО (для генеральной совокупности):

   

   Стандартное отклонение выражается в тех же единицах измерения, что и характеризуемый им признак.

   Коэффициент вариации

5. Одним из относительных показателей вариации является коэффициент вариации. Этот показатель представляет собой среднее квадратическое отклонение, выраженное в процентах от величины сред ней арифметической:

   

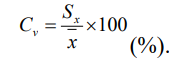
   Различные признаки характеризуются различными коэффициентами ва риации. Но в отношении одного и того же признака значение этого показате ля Cv остается более или менее устойчивым и при симметричных распреде лениях обычно не превышает 50%. При сильно асимметричных рядах рас пределения коэффициент вариации может достигать 100% и даже выше. Ва рьирование считается слабым, если не превосходит 10%, средним, когда Cv составляет 11-25%, и значительным при Cv>25%.

   Иногда коэффициент вариации используется и как показатель однород ности выборочных наблюдений. Критериальным значением коэффициента вариации Cv служит 0,333 или 33,3 %, то есть если Cv меньше или равен 0,333 – вариация считает слабой, а если больше 0,333 – сильной. В случае сильной вариации изучаемая статистическая совокупность считается неоднородной, а средняя величина – нетипичной и ее нельзя использовать как обобщающий показатель этой совокупности.

   Мода. Медиана. Процентили

Медиана (Ме) – это средняя величина, относительно которой вариаци онный ряд распределения делится на две половинки.

Мода (Мо) – величина, которая встречается в данной совокупности наиболее часто.

Перцентиль (процентиль) (Pi) – величина, отделяющая 1 /100 всех членов ряда. Девяносто девять перцентилей делят весь вариацион ный ряд на сто равных частей.