
федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский университет «Московский институт электронной техники».
Курсовая работа
Часть 1
Выполнил студент:
Проверил:
Задание 1
Дано:

1) = 22
= 22

2)

3)

4)
5)

6)

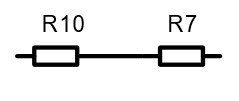
Задание 2



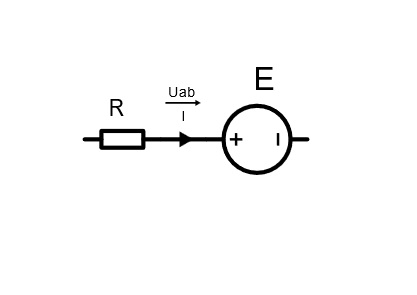
Задание 3
Дано: E1 =7В, E2=8В, E3=4В, I1=1,5A, I2=2A, I3=2A, R1=14 Ом, R2=6 Ом, R4=7 Ом, R5=8 Ом, R6=9 Ом.
А) Метод Эквивалентных преобразований
 (Направлен от узла
B
в узел А)
(Направлен от узла
B
в узел А)
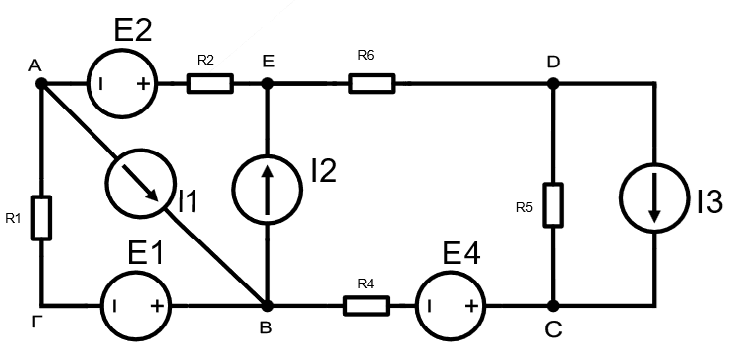
1)
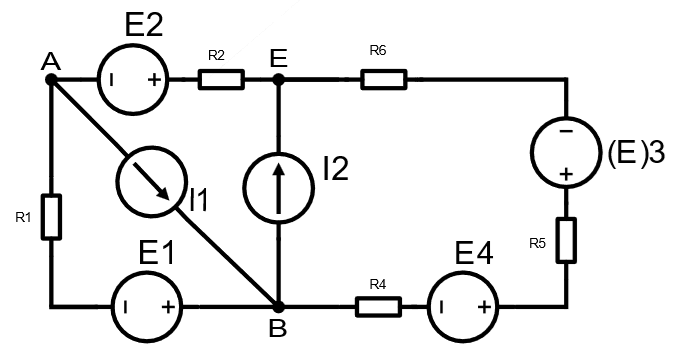
2)
3)
4)

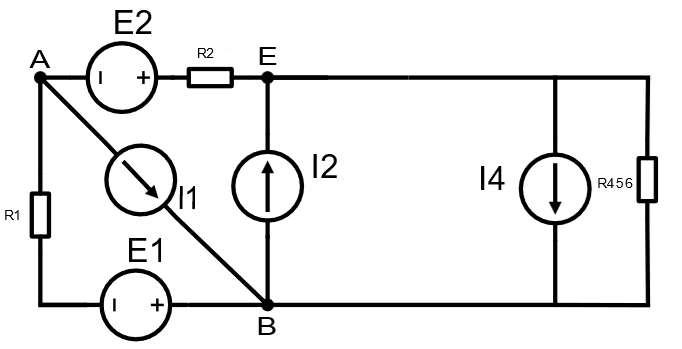
5)

6)
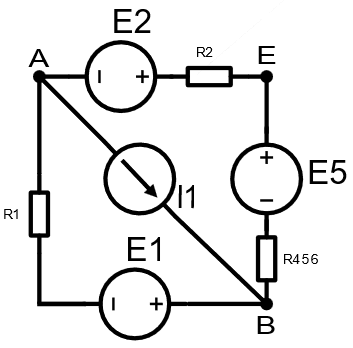
7)
8)
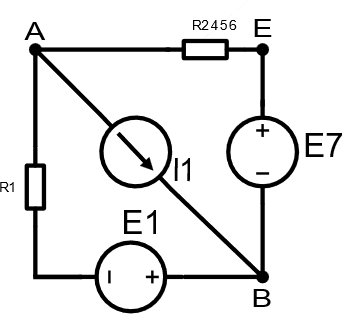
9)
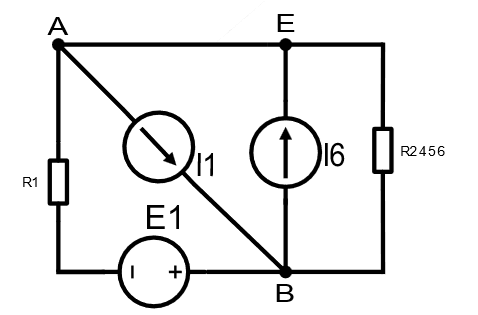
10)

11)

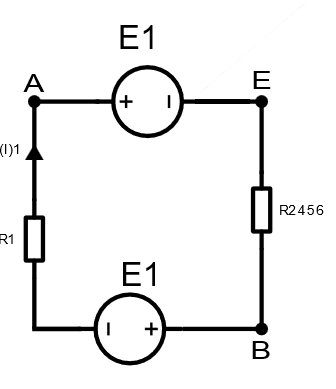
И
в итоге по второму закону Кирхгофа :

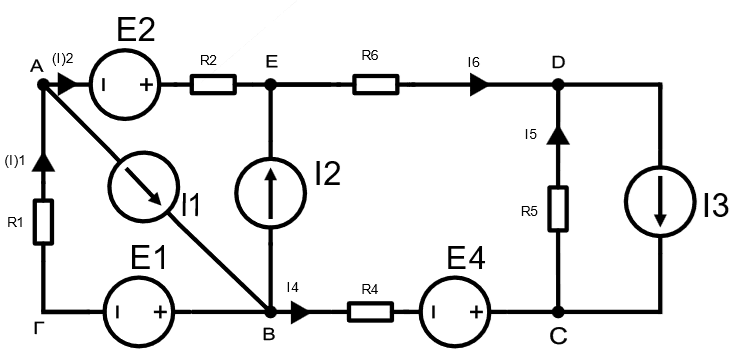
Б) Через законы Кирхгофа
Количество ветвей N = 8
Количество узлов n = 5
Количество источников силы тока t = 3
1) Первый закон Кирхгофа

Где m=n-1=4
2) Второй закон Кирхгофа

Где K – количество ЭДС в замкнутом контуре, М – количество элементов, на которые падает напряжение.
Количество уравнений для второго закона Кирхгофа Q = N – n – t = 1
Составим уравнения для АЕDCBГA. Обход по часовой стрелке

Решая данную систему, находим токи в ветвях:
I4=-0,73 A, I6=0,73 A, I2/=-1,27 A, I/1= 0,23 A, I5=1,27 A
В) Метод Контурных Токов(МКТ)

Количество уравнений для МКТ = N – n - = 1
Составим уравнения для АЕDCBГA. Обход по часовой стрелке
Ток I1 направим по контуру ВГАГ, Ток I2 направим по контуру EDCBE, Ток I3 направим по контуру DCD. Тогда:
 (1)
(1)

Решая
(1), получаем:

Исходя
из направления токов
 ,
находим токи в ветвях
,
находим токи в ветвях





Г) Метод узловых потенциалов. (МУП)
Количество уравнений L = n – 1 = 4
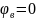
 ,
,

 ,
, ,
,

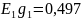
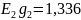

Составим матрицу

Решая
матрицу, находим :

Исходя из общего Закона Ома составляем уравнения для токов в ветвях и решаем их:


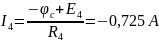


Д) Метод эквивалентного генератора
Хотим найти ток в ветви АВ. Для этого ее отсоединим.
методом эквивалентных преобразований найдем Uab. Собственно, задача сводится к пункту а), поэтому все вычисления в данном методе эквиваленты вычислениям в пункте а)
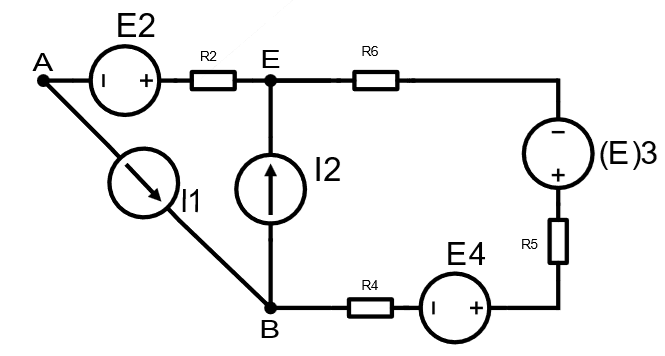
В результате Получаем

Е)Результаты, полученные разными методами:
|
МЭП |
З.К |
МКТ |
МУП |
МЭГ |
|
0,22 |
0,22 |
0,23 |
0,22 |
0,22 |
|
- |
-1,27 |
-1,27 |
-1,27 |
- |
|
- |
-0,725 |
-0,73 |
-0,73 |
- |
|
- |
1,27 |
1,27 |
1,27 |
- |
|
- |
0,73 |
0,73 |
0,73 |
- |
Ё) Построим векторно-потенциальную диаграмму для контура АЕDCBГA








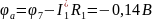

Ж) Баланс Мощностей
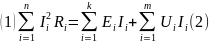 Где
в нашем случае:
n=5,
k
= 3, m
= 3
Где
в нашем случае:
n=5,
k
= 3, m
= 3




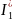 ,
А
,
А ,А
,А ,
А
,
А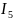 ,
А
,
А ,
А
,
А