Федеральное Агентство Связи Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики»

Центр заочного обучения по программам бакалавриата

Кафедра «Мультимедийных сетей и услуг связи»

Дисциплина: Мультимедийные информационные системы

Практическая работа №2

Выполнил: Иванов И.И., студент группы БСТ17XX Вариант №7

Проверил:

Москва, 2021

Содержание

Задача №1

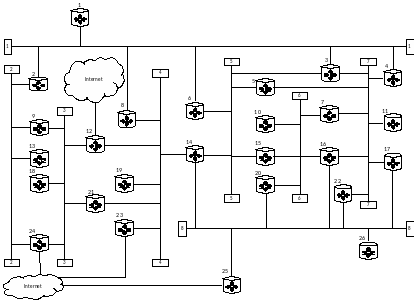
В соответствии с вариантом взять исходные данные из табл. 8 и найти маршрут самого быстрого прохождения пакета от маршрутизатора с номером 1 до выхода с маршрутизатора с номером 25 (рисунок 1), применяя алгоритм Дейкстры.

При прохождении через сеть Интернет пакеты обрабатываются на интерфейсах маршрутизаторов со скоростью 170 пакетов/с.

Пакеты всегда идут от маршрутизатора с меньшим номером к маршрутизатору с большим номером. Например, с маршрутизатора 9 пакеты могут быть переданы на маршрутизаторы 12, 13, 18, 21, 24 и не могут быть переданы на маршрутизатор 2.

Если маршрутизатор имеет прямое подключение к сети Интернет, то он может как посылать пакеты в сеть Интернет, так и получать их из сети Интернет.

Построить граф сети, указать на нем кратчайший маршрут и время затраченное на его прохождение

Скорость обработки пакетов Пакет/с	Маршрутизатор №	№ Варианта
		7
	1	13650
	2	12150
	3	13150
	4	12650
	5	12400
	6	12900
	7	9400
	8	11400
	9	10900
	10	14400
	11	10650
	12	11150
	13	9900
	14	11900
	15	9150
	16	14900
	17	13900
	18	11650
	19	9650
	20	14650
	21	10150
	22	13400
	23	10400
	24	14150
	25	8900

Для нахождения кратчайшего маршрута воспользуемся программой на python.

Введем в программу веса ребер и отношения между вершинами

# Веса ребер

speed = {

1: 1/13650,

2: 1/12150,

3: 1/13150,

4: 1/12650,

5: 1/12400,

6: 1/12900,

7: 1/9400,

8: 1/11400,

9: 1/10900,

10: 1/14400,

11: 1/10650,

12: 1/11150,

13: 1/9900,

14: 1/11900,

15: 1/9150,

16: 1/14900,

17: 1/13900,

18: 1/11650,

19: 1/9650,

20: 1/14650,

21: 1/10150,

22: 1/13400,

23: 1/10400,

24: 1/14150,

25: 1/8900

}

# Отношения между вершинами

G = {

1: {2:speed[1], 3:speed[1], 4:speed[1], 6:speed[1], 8:speed[1]},

2: {3:speed[2], 4:speed[2], 6:speed[2], 8:speed[2], 9:speed[2], 13:speed[2], 24:speed[2]},

3: {4:speed[3], 5:speed[3], 6:speed[3], 7:speed[3], 8:speed[3], 11:speed[3], 14:speed[3], 15:speed[3], 16:speed[3], 17:speed[3], 22:speed[3]},

4: {5:speed[4], 6:speed[4], 7:speed[4], 8:speed[4], 11:speed[4], 16:speed[4], 17:speed[4], 22:speed[4]},

5: {6:speed[5], 7:speed[5], 11:speed[5], 14:speed[5], 15:speed[5], 16:speed[5], 17:speed[5], 22:speed[5]},

6: {8:speed[6], 14:speed[6], 15:speed[6]},

7: {10:speed[7], 11:speed[7], 15:speed[7], 16:speed[7], 17:speed[7], 20:speed[7], 22:speed[7]},

8: {12:speed[8], 14:speed[8], 19:speed[8], 21:speed[8], 23:speed[8]},

9: {12:speed[9], 13:speed[9], 18:speed[9], 21:speed[9], 24:speed[9]},

10: {15:speed[10], 16:speed[10], 20:speed[10]},

11: {16:speed[11], 17:speed[11], 22:speed[11]},

12: {14:speed[12], 18:speed[12], 19:speed[12], 21:speed[12]},

13: {24:speed[13]},

14: {15:speed[14], 16:speed[14], 19:speed[14], 20:speed[14], 21:speed[14], 22:speed[14], 23:speed[14], 25:speed[14]},

15: {16:speed[15], 20:speed[15]},

16: {17:speed[16], 20:speed[16], 22:speed[16], 25:speed[16]},

17: {20:speed[17], 22:speed[17], 25:speed[17]},

18: {21:speed[18], 24:speed[18]},

19: {21:speed[19], 23:speed[19]},

20: {22:speed[20], 25:speed[20]},

21: {24:speed[21], 23:speed[21]},

22: {25:speed[22]},

23: {},

24: {},

25: {}

}

Ответ: Кратчайший маршрут 1-3-16-25, с временем прохождения маршрута 0.00021641979459623064