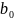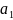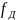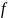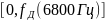111Equation Chapter 1 Section 1министерство цифрового развития, связи и массовых коммуникаций российской федерации

Ордена Трудового Красного Знаменитости федеральное государственное бюджетное образовательное учреждение наивысшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

СВЯЗИ И ИНФОРМАТИКИ

──────────────────────────────────────

Факультет СиСС

Кафедра ОТС

ЛАБОРАТОРНАЯ РАБОТА 

№ 26, 2

по дисциплине «Цифровая обработка сигналов»

на тему:

«Анализ рекурсивных цифровых фильтров

1-го и 2-го порядка»

Вариант №18

                                                                             Выполнил:

                                                                               Проверил: проф. кав. ОТС

                                                                                                             Волчков В. Н.

(Летний семестр)

Москва 2023 

1. Цели работы

Провести экспериментальный анализ рекурсивных цифровых фильтров (ЦФ) 1-го и 2-го порядка; исследовать частотные и временные характеристики фильтров, их взаимосвязь со значениями коэффициентов ЦФ; определить области устойчивости рекурсивных фильтров 1, 2, 3 и четвертого порядка.

2. Выполнение Д/З

2.1 Исходные данные вариантов

Табл. 1. Таблица значений параметров фильтра

номер Варианта	18
Параметр:	1
Параметр:	0,5
	6800 Гц

2.2 Запись разностного уравнения и системной функции

Разностное уравнение рекурсивного ЦФ-1 (первого порядка) имеет вид:

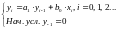22\* MERGEFORMAT ()

Построение системной функции :

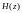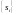
Пусть задан дискретный квантованный сигнал к 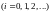, тогда его односторонним 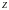- преобразованием называется:

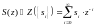33\* MERGEFORMAT ()

Свойства - преобразования:

Свойство 1 (линейности):

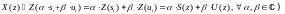44\* MERGEFORMAT ()

Свойство 2 (смещения):

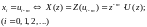55\* MERGEFORMAT ()

Пусть на входе ЦФ(цифро-фильтра) действует сигна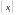л , а на его выходе наблюдается сигнал 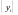, тогда системной функцией ЦФ называется отношение:

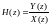66\* MERGEFORMAT ()

Находим 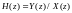применив к обеим частям уравнения (1) Z преобразование и воспользовавшись свойствами линейных помех и смещения (свойство 1 и свойство 2):

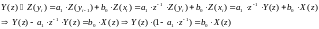77\* MERGEFORMAT ()

Отсюда получаем:

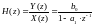88\* MERGEFORMAT ()

Вывод - нет сигнала.

2.3 Структурная схема цф

Структурная схема цифрового фильтра строится на основе развернутого уравнения (1). Ниже представлена структурная схема рекурсивного ЦФ 1-го беспорядка:

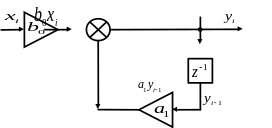
Рис. 1. Структурная схема рекурсивного ЦФ 1-го порядка

( )

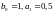2.4 Расчёт и построение импульсной реакции, переходной характеристики, амплитудно-частотной характеристики и фазо-частотной характеристики цф

Ниже представлена схема получения импульсной характеристики ЦФ:

Рис. 2. Схема получения ИХ

По определению ИХ (см. рис. 2):

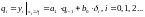99\* MERGEFORMAT ()

где 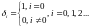1010\* MERGEFORMAT ()

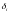– единичный импульс Кронекера

Из (8) с учётом начального условия и (9) последовательно получаем:

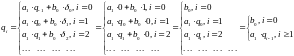1111\* MERGEFORMAT ()

Ниже представлена импульсная характеристика ЦФ 1-го порядка:

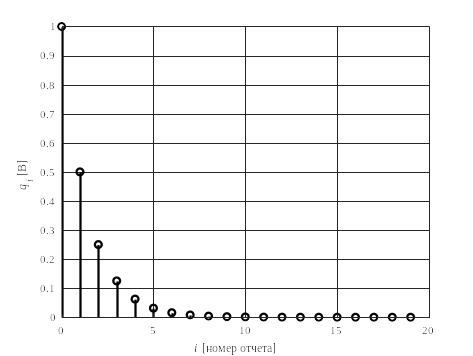
Рис. 3. Импульсная характеристика ЦФ 1-го порядка

( )

Ниже представлена схема получения переходной характеристики ЦФ:

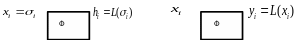
Рис. 4. Схема получения ПХ

Переходной функцией 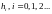цифрового фильтра называется его отклик на дискретный единичный скачок:

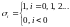1212\* MERGEFORMAT ()

По определению фильтр называется устойчивым если по ограниченному входному воздействии 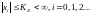его выход (отклик) также ограничен, т.е.

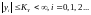
Следовательно, из определения выше следует, что для устойчивости ЦФ при действии на входе 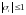на выходе получаем .

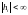Из (11) следует, что:

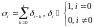1313\* MERGEFORMAT ()

Любой ЦФ является дискретной линейной системой, действие которого на входной сигнал 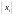описывается линейным оператором 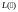. Это означает, что выходной сигнал есть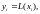 а если 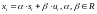, то

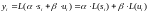1414\* MERGEFORMAT ()

Выражение (13) описывает свойство нелинейности. Следовательно, если 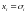, то из (12) и (13) имеем:

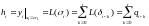1515\* MERGEFORMAT ()

Делаем замену переменных

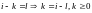
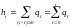1616\* MERGEFORMAT ()

Из (15) c учётом (10) получаем:

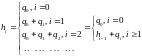1717\* MERGEFORMAT ()

Отсюда получаем метод построения 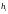. Сначала, зная уравнение ЦФ строим ИХ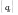 , затем по формуле (16) строим :

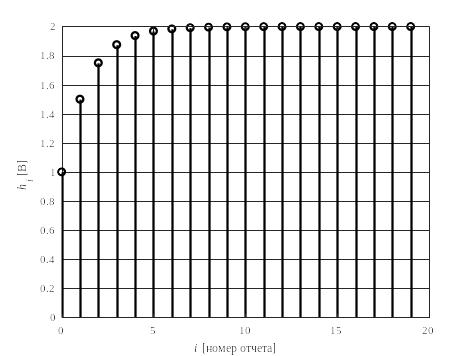
Рис. 5. Переходная характеристика ЦФ первого порядка (неполная синусоида)

( )

Нахождение комплексного коэффициента передачи:

Комплексным коэффициентом передачи ЦФ 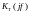называется функция чистоты :

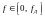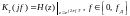1818\* MERGEFORMAT ()

где 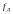– частота дискретизации, 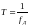– интервал дискретизации

Свойства комплексных чисел:

Если 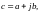то

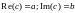1919\* MERGEFORMAT ()

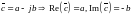2020\* MERGEFORMAT ()

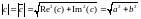2121\* MERGEFORMAT ()

Если 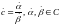- комплексная дробь, то справедливо:

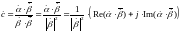2222\* MERGEFORMAT ()

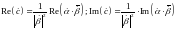2323\* MERGEFORMAT ()

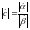2424\* MERGEFORMAT ()

Формулы Эйнштейна:

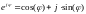2525\* MERGEFORMAT ()

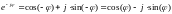2626\* MERGEFORMAT ()

Находим используя (17) и формулы Эйнштейна (24), (25):

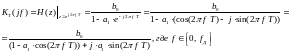2727\* MERGEFORMAT ()

Находим Re и Im от с учётом (21), (22), (23):

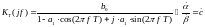2828\* MERGEFORMAT ()

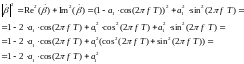2929\* MERGEFORMAT ()

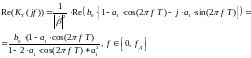3030\* MERGEFORMAT ()

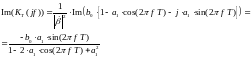3131\* MERGEFORMAT ()

Нахождение АЧХ:

Амплитудно-чистой характеристикой (АЧХ) ЦФ, называется функцией чистоты:

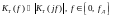3232\* MERGEFORMAT ()

Находим АЧХ 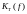по формуле (31) и с учётом (23):

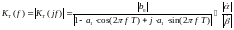3333\* MERGEFORMAT ()

Преобразуем знаменатель с учётом полученного ранее 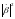в формуле (28):

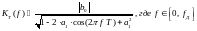3434\* MERGEFORMAT ()

Ниже представлена амплитудно-частотная характеристика ЦФ 1-го порядка:

Рис. 6. АЧХ ЦФ 1-го порядка (сигнал ослабляется до 4кГц, но потом усиливается до 8 кГц)

( )

Нахождение ФЧХ:

Фразо-частотной характеристикой (ФЧХ) цифрового фильтра называется функция чистоты:

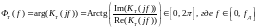3535\* MERGEFORMAT ()

Находим ФЧХ 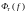по формуле (34), используя (29), (30):

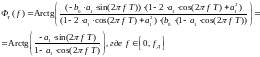3636\* MERGEFORMAT ()

Ниже представлена фазо-частотная характеристика ЦФ 1-го порядка:

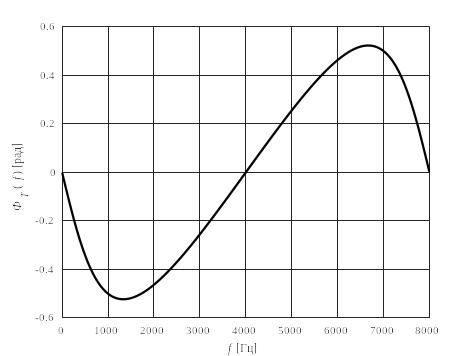
Рис. 7. ФЧХ ЦФ 1-го порядка

( )