Рассчитать зависимости удельного сопротивления и температурного
коэффициента удельного сопротивления от состава для сплавов системы Cu- при комнатной температуре:
Использую формулу ρCu- = ρх + ρСu (1−х) + С х(1−х),
Коэффициент С вычисляю, подставляя значения из 1 пункта обработки, принимая, что содержание никеля x = 0.4 в относительных долях по массе х + хCu = 1.
=
=
2.16 * 10-6
Рассчитываю удельное сопротивление
ρCu-Ni
=
+
(1−0)
+ 2.16
* 10-6*0(1−0)
= 0.016
* 10-6
ρCu-Ni
=
2
+
(1−0.2)
+ 2.16
* 10-6*0.2(1−0.2)
= 0.3744
* 10-6
ρCu-Ni = 6 + (1−0.6) + 2.16 * 10-6*0.6(1−0.6) = 0.3812 * 10-6
ρCu-Ni = 8 + (1−0.8) + 2.16 * 10-6*0.8(1−0.8) = 0.5684 * 10-6
ρCu-Ni
=
1.0
+
(1−1.0)
+ 2.16
* 10-6*1.0(1−1.0)
= 0.0800 * 10-6
Заношу в таблицу
хNi |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
ρ , мкОм.м |
0.016 |
0.3744 |
0.5600 |
0.5684 |
0.4128 |
0.0800 |
αρ , К-1 |
0.00230 |
0.00028 |
0.00031 |
0.00043 |
0.0076 |
0.00480 |
Рассчитываю тепловой коэффициент удельного сопротивления сплавов
Используя
:
=
0.00230 K-1
=
0.00028 K-1
=
0.00031 K-1
=
0.00043 K-1
=
0.00076 K-1
=
0.00480 K-1
Построение графиков зависимости ρ(x) и αρ(x)
Рисунок 9 - График зависимости удельного сопротивления сплава от состава
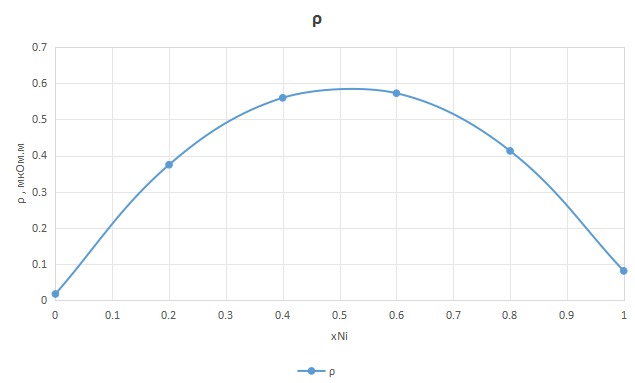
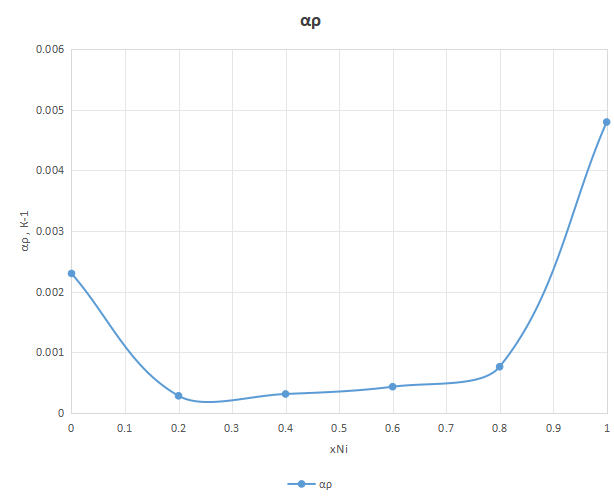
Рисунок 10 - График зависимости теплового коэффициента удельного сопротивления от состава
Построение графиков зависимости ΔU(Δt ):
t, C |
Δt, C |
ΔU, мВ |
||
Медь-железо |
Медь-константан |
Медь-манганин |
||
26 |
86 |
-0.09 |
-0.08 |
-0.07 |
40 |
100 |
0.4 |
0.38 |
-0.06 |
54 |
114 |
0.86 |
0.83 |
-0.06 |
68 |
126 |
1.23 |
1.25 |
-0.04 |
82 |
-25 |
1.61 |
1.1 |
-0.02 |
96 |
-25 |
1.99 |
2.16 |
-0.02 |
110 |
84 |
2.36 |
2.62 |
0 |
124 |
-26 |
2.72 |
3.11 |
0.03 |
138 |
112 |
3.08 |
3.64 |
0.03 |
150 |
123 |
3.35 |
4.04 |
0.03 |
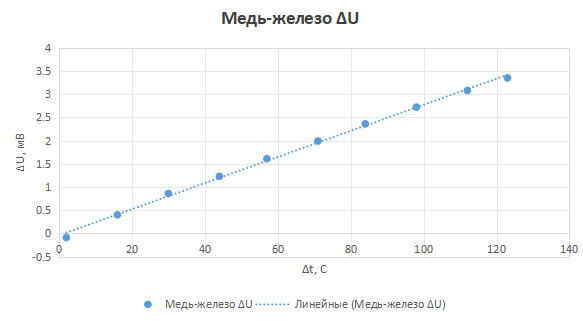
Рисунок 11 - График зависимости ΔU(Δt ) для сплава медь-железо
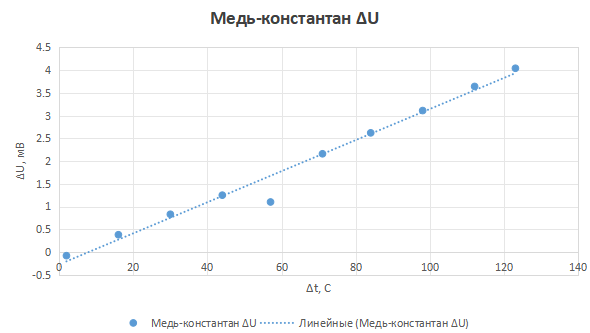
Рисунок 12 - График зависимости ΔU(Δt ) для сплава медь-константан
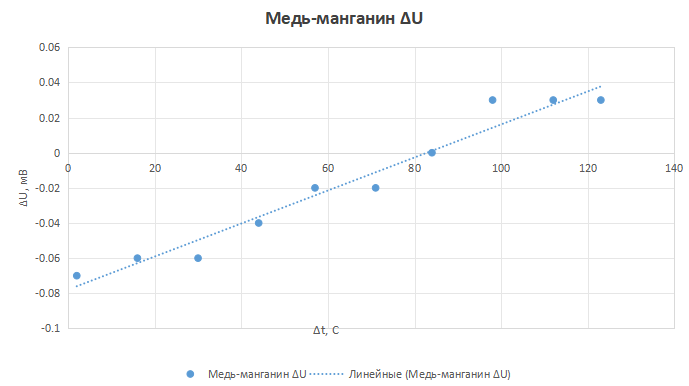
Рисунок 13 - График зависимости ΔU(Δt ) для сплава медь-манганин
Вывод: В ходе выполнения работы было выяснено:
С повышением температуры, сопротивление меди и никеля заметно повышаются, в отличие от сопротивления константана, которое понижается на очень малое значение, так как в его структуре очень малое количество дефектов.
Удельное сопротивление нихрома больше удельных сопротивлений остальных рассматриваемых металлов, так как это сплав и в нем большое количество статических дефектов.
Сопротивление квадрата поверхностной металлической пленки материала 1 превышает сопротивления остальных рассматриваемых плёнок так как он имеет наименьший квадрат поверхности и сопротивление распределяется более концентрировано.
Удельное сопротивление сплава металлов намного больше удельного сопротивления входящие в состав металлов по отдельности, так как в них больше присутствие статических дефектов.
Максимум удельного сопротивления сплава достигается при равных значениях концентраций составляющих его металлов, потому что после этого порога один из металлов становится чище и сопротивление падает.