1.4. Анализ цепи при гармонических функциях источника в комплексной области

а) Преобразовать исходную схему электрической̆ цепи, где необходимо исключить источники напряжения e1(t), e2(t), e3(t) и преобразовать в схеме «звезду» в «треугольник».

б) Получить формулы для входного сопротивления со стороны узлов 1, 0, а также выражение для передаточной̆ функции на узлах 3,0.

Получение этих выражений следует провести с помощью пакета MATHCAD.

в) Построить частотные характеристики по полученным выражениям входного сопротивления и передаточной функции в указанном пакете программ. Первый̆ диапазон частот брать от нуля до до 5000 рад/с. Провести уточнение диапазона частот каждому студенту индивидуально с целью представления частотных характеристик наиболее информативно. Графики АЧХ и ФЧХ делать в едином масштабе для совмещения и изучения хода кривых в локальных экстремумах. Выделить в другом масштабе участки графиков, где наблюдаются локальные экстремумы кривых

г) Проверить частотные характеристики входного сопротивления и передаточной̆ функции, используя программу схемотехнического моделирования MICRO-CAP.

Каждому значению частоты, для которого существует локальный экстремум, поставить в соответствие эквивалентную схему резонанса напряжений или резонанса токов.

д) Полученные частотные характеристики объяснить с помощью эквивалентных моделей̆ схемы в виде звезды и без источников напряжения.

Преобразуем исходную схему в такую, где отсутствуют источники тока (схема 1.4.1)

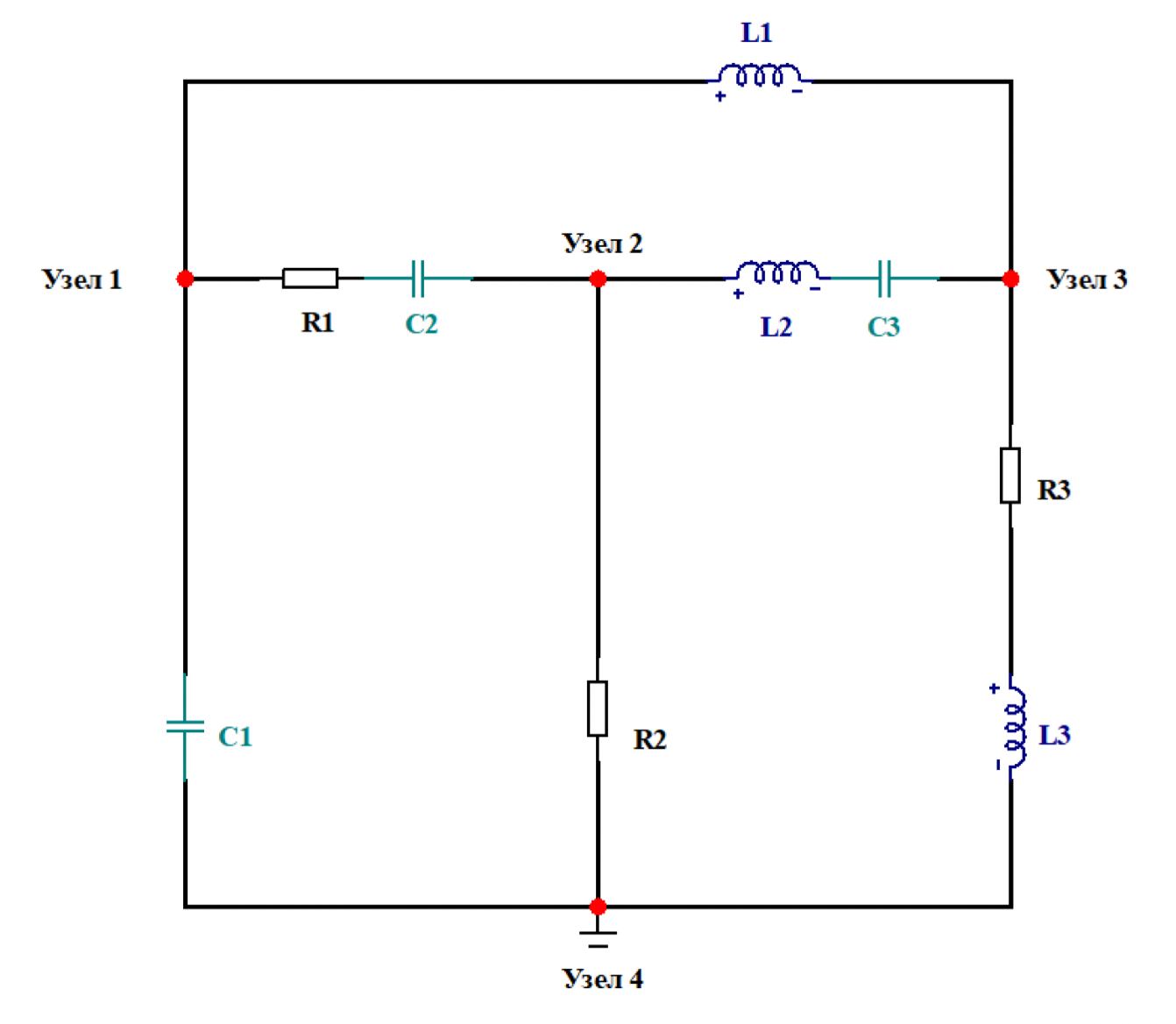
Схема 1.4.1 – Упрощённая схема (без источников тока).

Упрощаем схему из «звезды» в «треугольник» (схема 1.4.2.1 – 1.4.2.3)

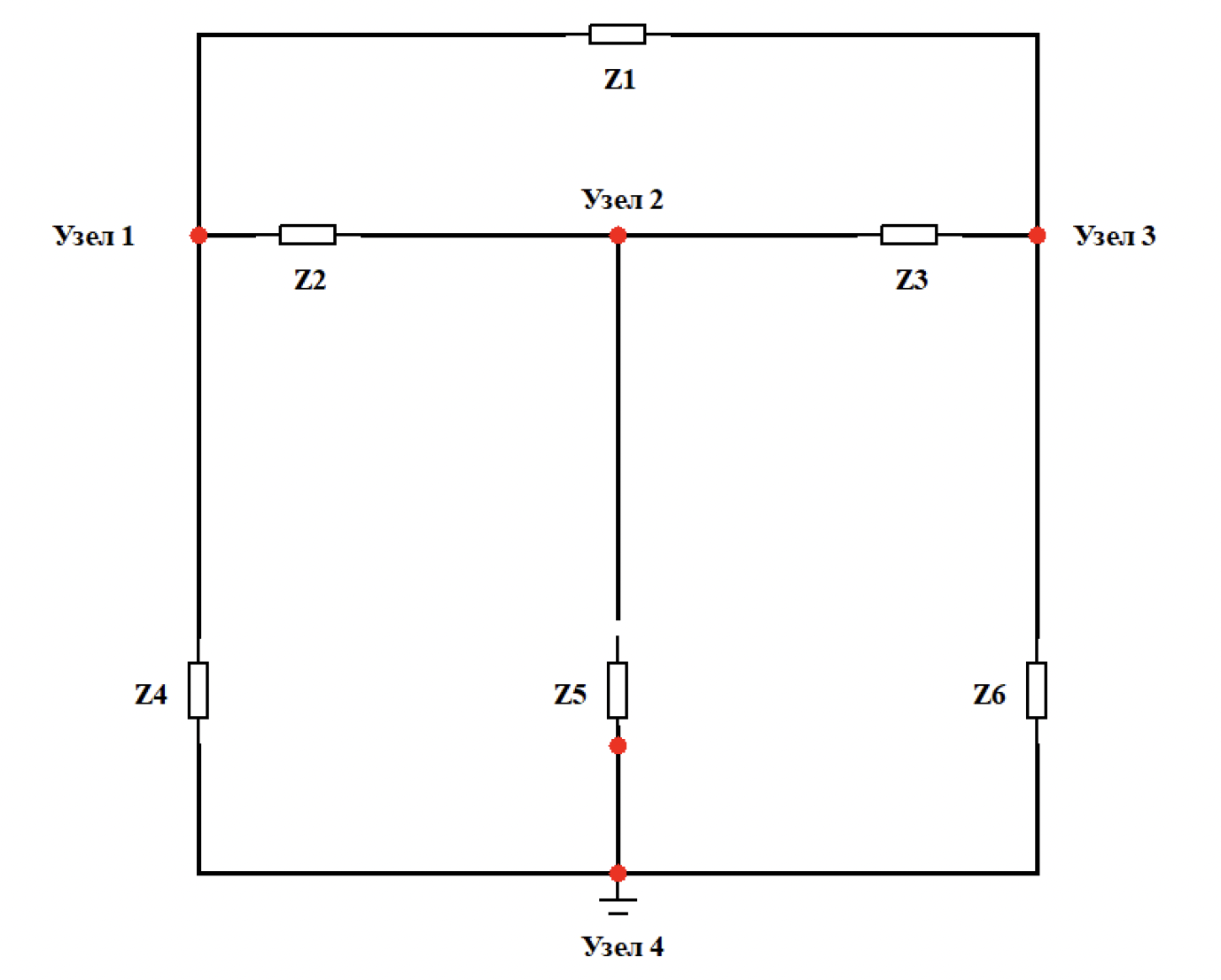
Схема 1.4.2.1 – «Из звезды» в «треугольник» (шаг 1)

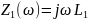
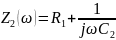
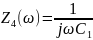
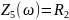
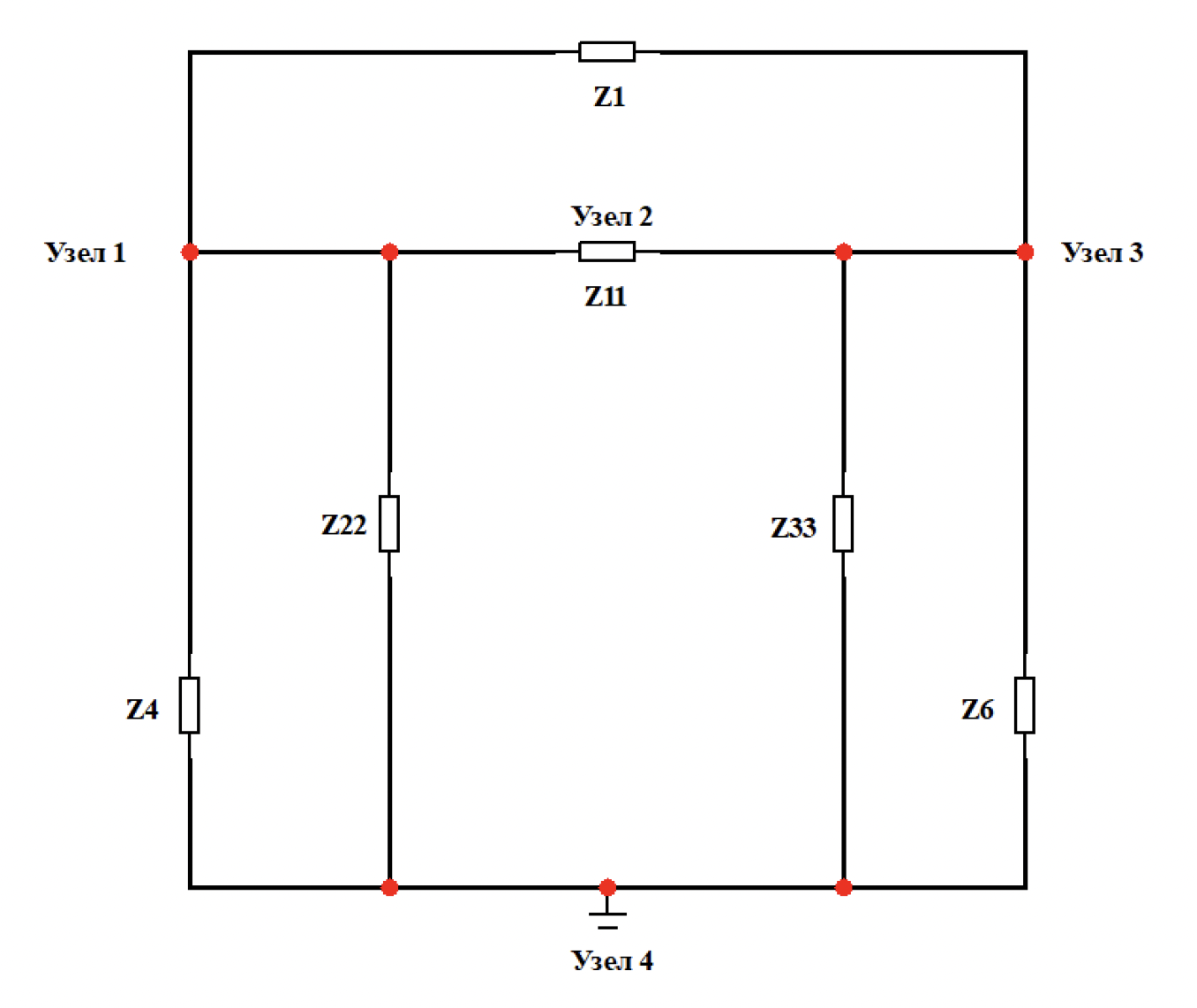
Схема 1.4.2.2 – «Из звезды» в «треугольник» (шаг 2)

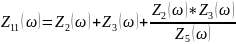
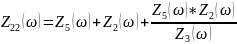
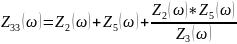
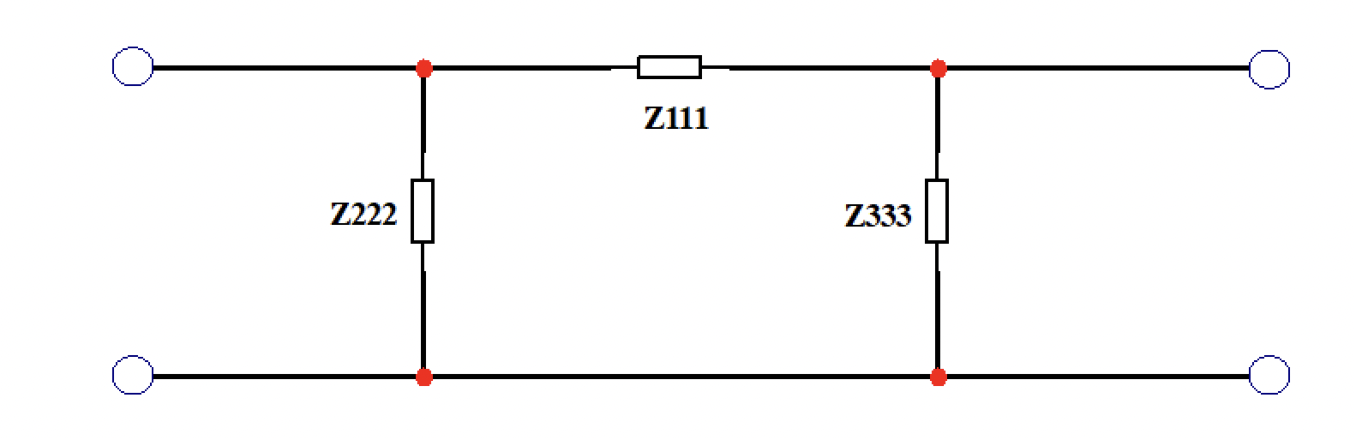
Схема 1.4.2.3 – «Из звезды» в «треугольник» (шаг 3)

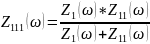
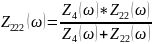
Ниже указаны формулы и схема для построения необходимых графиков зависимостей с помощью программ Mathcad и Microcap (схема 1.4.3)

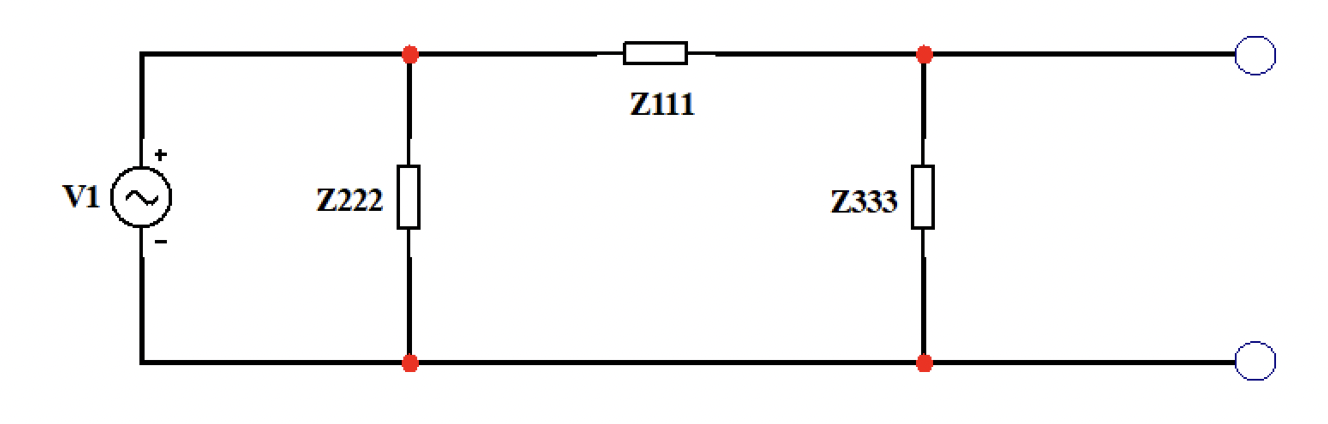
Схема 1.4.3 – Схема, используемая для расчётов.

Ниже показаны формулы, используемые для расчётов.

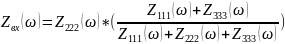
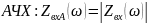
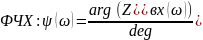
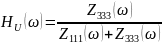
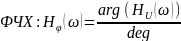
На рисунке 6 показаны графики АЧХ и ФЧХ 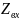от 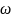(принято от 10 до 500)

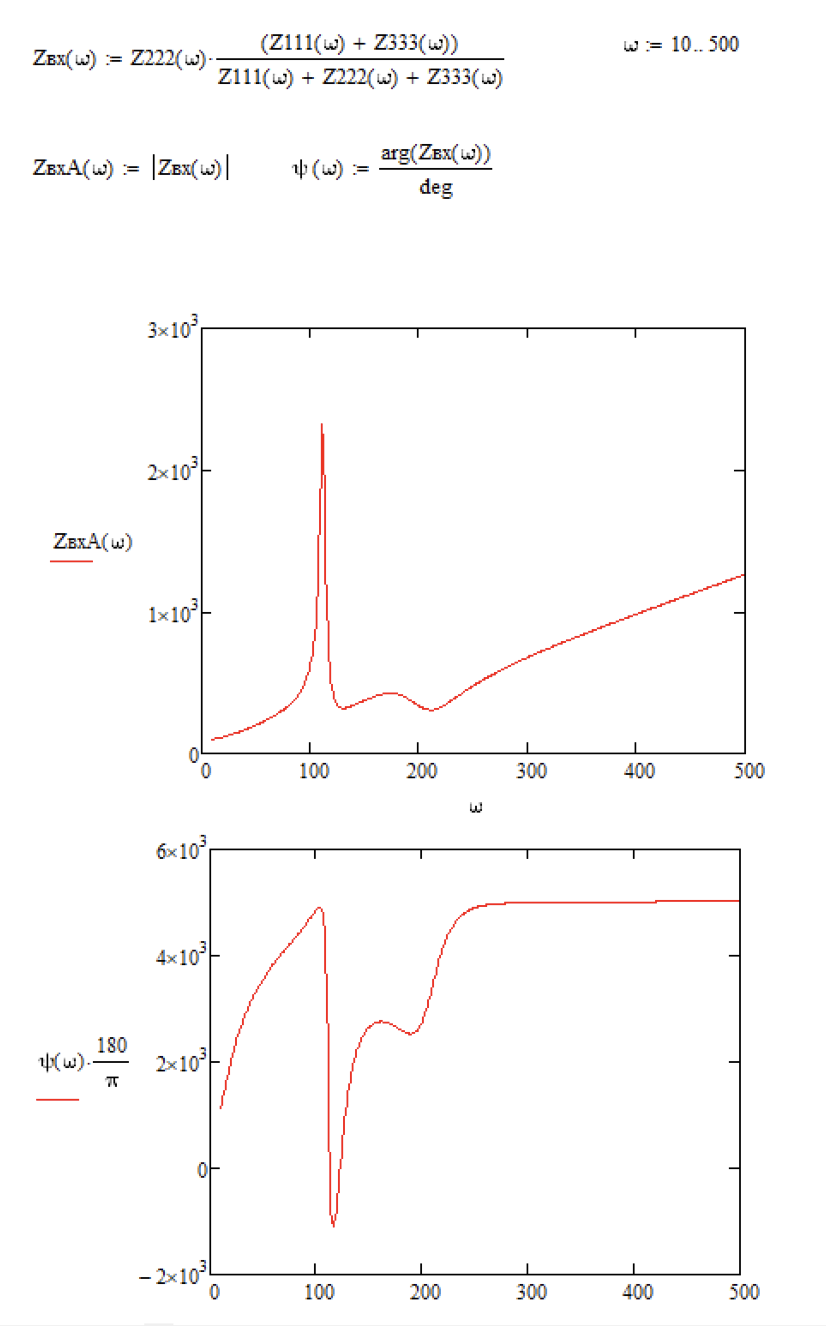
Рисунок 6. – Графики зависимости от .

На рисунке 7 показаны графики АЧХ и ФЧХ 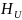от (принято от 10 до 500)

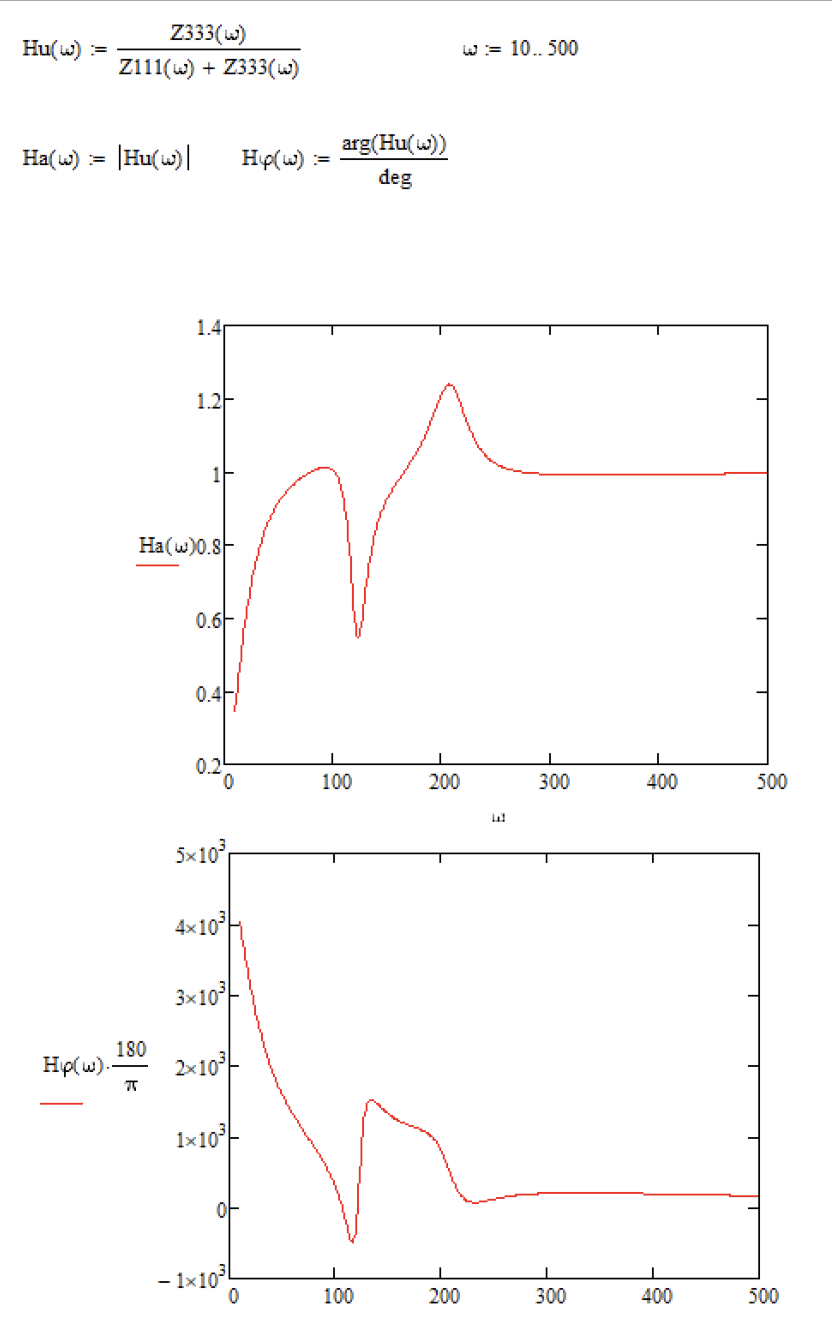
Рисунок 7. – Графики зависимости от .

На рисунке 8 показаны сопоставления вышеописанных графиков АЧХ и ФЧХ для и соответственно.

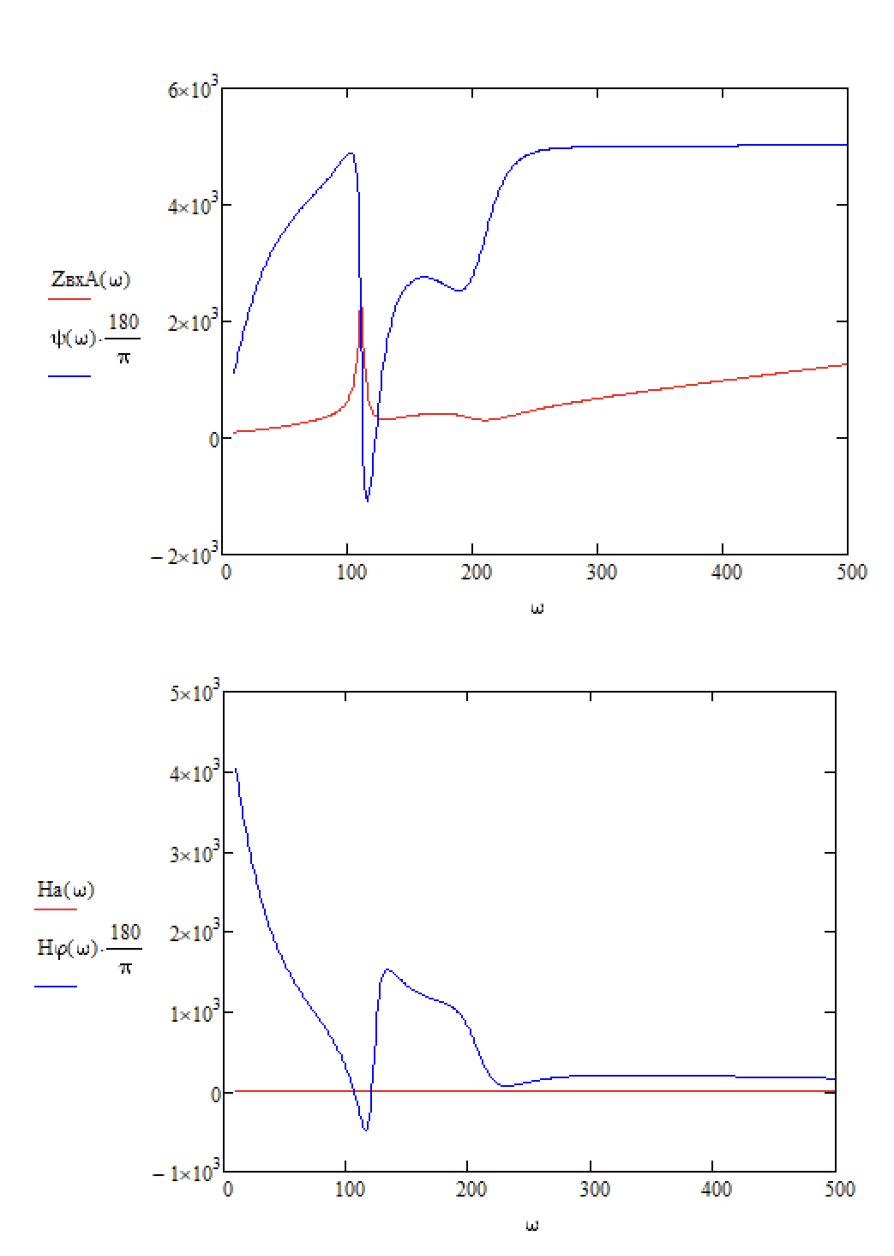
Рисунок 8. – Графики АЧХ и ФЧХ для и на одной плоскости.

На рисунке 9 показаны графики АЧХ и ФЧХ, нарисованные в программе Microcap.

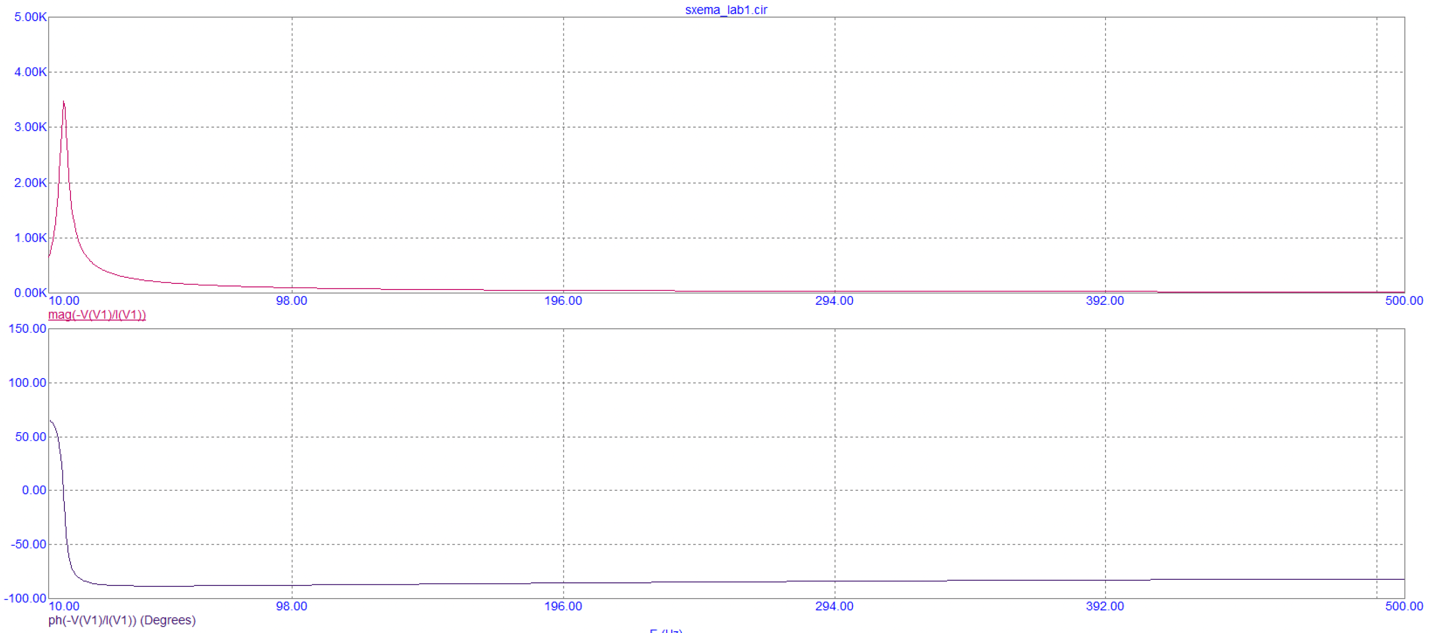
Рисунок 9. – Графики АЧХ и ФЧХ в программе Microcap.

На рисунке 10 показаны графики АЧХ и ФЧХ, нарисованные в программе Microcap, но на одной координатной плоскости.

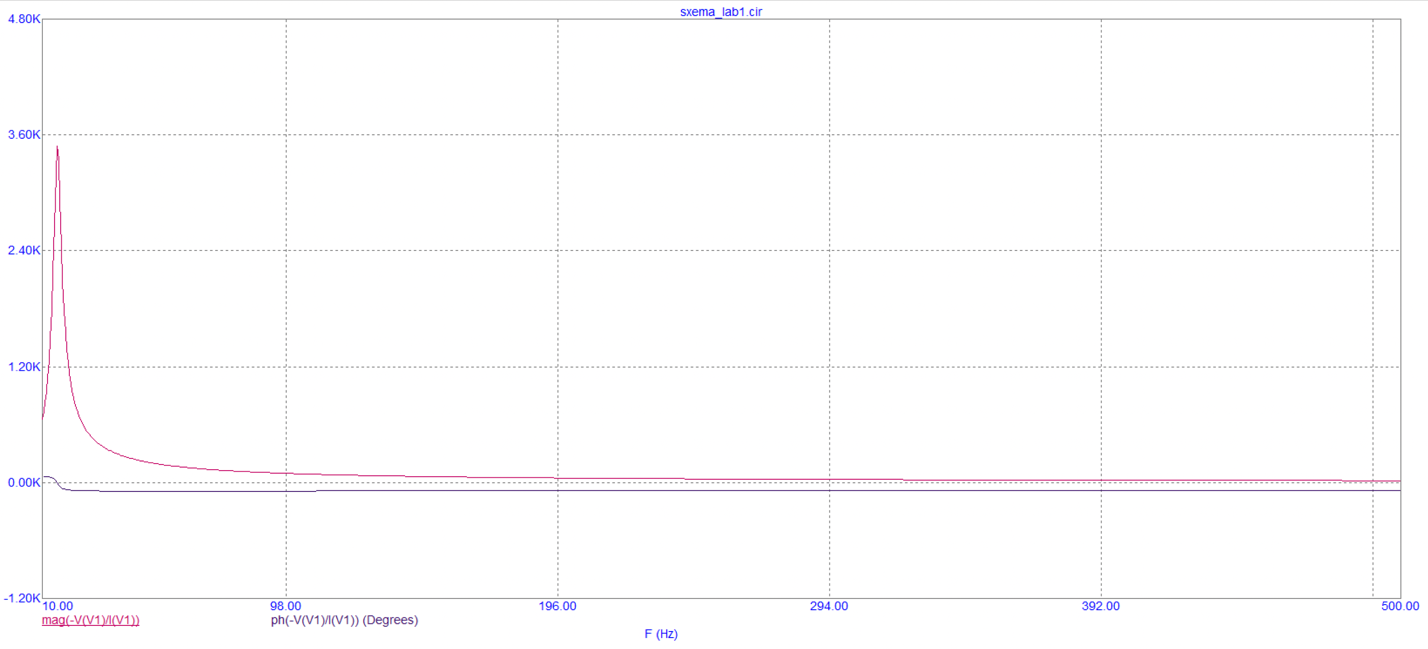
Рисунок 10. – Графики АЧХ и ФЧХ в программе Microcap на одной координатной плоскости.

ВЫВОД.

Был проведён анализ электрической цепи: найдены напряжения на катушках индуктивности, составлены матрицы сопротивлений в вещественном и комплексном виде, найдены значения токов и напряжений на элементах в комплексной, экспоненциальной и временной формах, построены графики в программах Mathcad и Microcap, доказаны первый и второй законы Кирхгоффа и проведены преобразования схем.