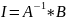МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ
КАФЕДРА ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
КУРСОВАЯ РАБОТА
АНАЛИЗ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Выполнил: студент группы XXXX https://t.me/mattervisualizer
Проверил: Заведующий кафедрой "Теория электрических цепей", Доктор технических наук, профессор Крейнделин. В. Б.
МОСКВА 2022 г.
СОДЕРЖАНИЕ.
1. ВВЕДЕНИЕ 3
1.1. АНАЛИЗ ЦЕПИ ПО ПОСТОЯННОМУ ТОКУ 5
1.2. АНАЛИЗ ЦЕПИ ПРИ ГАРМОНИЧЕСКИХ ФУНКЦИЯХ ИСТОЧНИКА В КОМПЛЕКСНОЙ ОБЛАСТИ 11
1.3. АНАЛИЗ ЦЕПИ ПРИ ГАРМОНИЧЕСКИХ ФУНКЦИЯХ ИСТОЧНИКА В КОМПЛЕКСНОЙ ОБЛАСТИ 18
1.4. АНАЛИЗ ЦЕПИ ПРИ ГАРМОНИЧЕСКИХ ФУНКЦИЯХ ИСТОЧНИКА В КОМПЛЕКСНОЙ ОБЛАСТИ 30
ВЫВОД. 40
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ. 41
1. ВВЕДЕНИЕ 3
1.1. АНАЛИЗ ЦЕПИ ПО ПОСТОЯННОМУ ТОКУ 5
1.2. АНАЛИЗ ЦЕПИ ПРИ ГАРМОНИЧЕСКИХ ФУНКЦИЯХ ИСТОЧНИКА В КОМПЛЕКСНОЙ ОБЛАСТИ 11
1.3. АНАЛИЗ ЦЕПИ ПРИ ГАРМОНИЧЕСКИХ ФУНКЦИЯХ ИСТОЧНИКА В КОМПЛЕКСНОЙ ОБЛАСТИ 18
1.4. АНАЛИЗ ЦЕПИ ПРИ ГАРМОНИЧЕСКИХ ФУНКЦИЯХ ИСТОЧНИКА В КОМПЛЕКСНОЙ ОБЛАСТИ 30
ВЫВОД. 40
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ. 41
Вариант №6.
1. Введение
Общий вид схемы электрической цепи показан на рисунке 1.
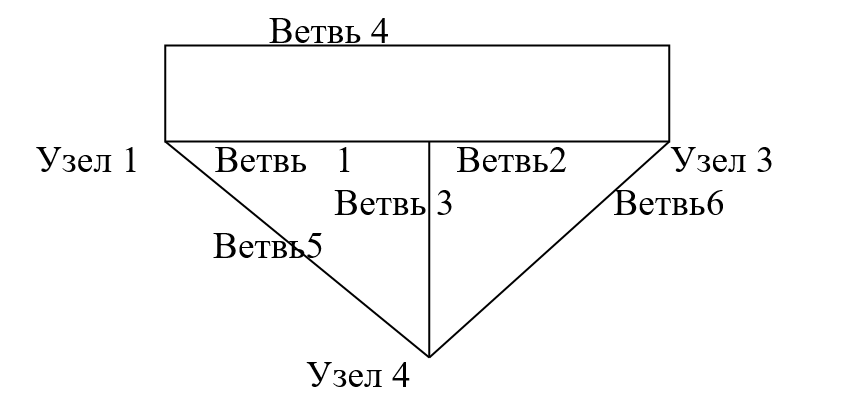
Рисунок 1. – Общий вид схемы электрической цепи.
Кодовая информация задания варианта №6 показана в таблице 1.
Таблица 1. – Кодовая информация задания.
Номер варианта |
6 |
Элемент кода |
6 |
Элемент кода |
1 |
Элемент кода |
2 |
Элемент кода |
3 |
Элемент кода |
4 |
Элемент кода |
5 |
Схема электрической цепи для варианта №6 представлена на схеме 1.
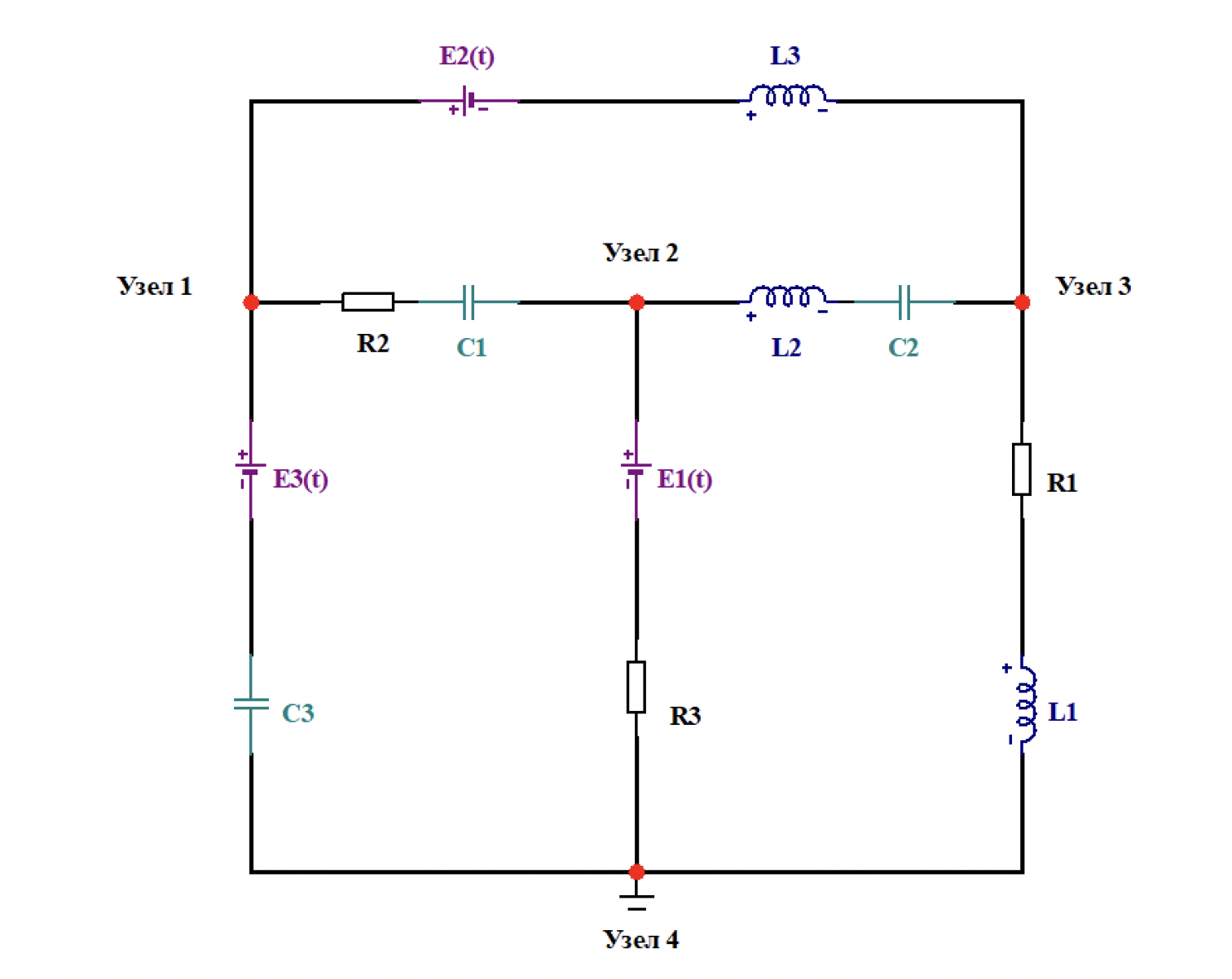
Схема 1. – Схема электрической цепи.
1.1. Анализ цепи по постоянному току
а)
Для получения схемы цепи постоянного
тока необходимо приравнять значение
частоты в выражениях
,
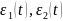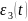нулю;
б) Полученное значение для ЭДС источников определить их, как источники постоянной ЭДС – , ;
в) Привести эквивалентные схемы цепи постоянного тока в двух случаях при подключении источников и при t → ∞.
Схема электрической цепи c обозначенными направлениями эл. тока для варианта №6 представлена на схеме 1.1.1. Напряжение присутствует только на катушках индуктивности.
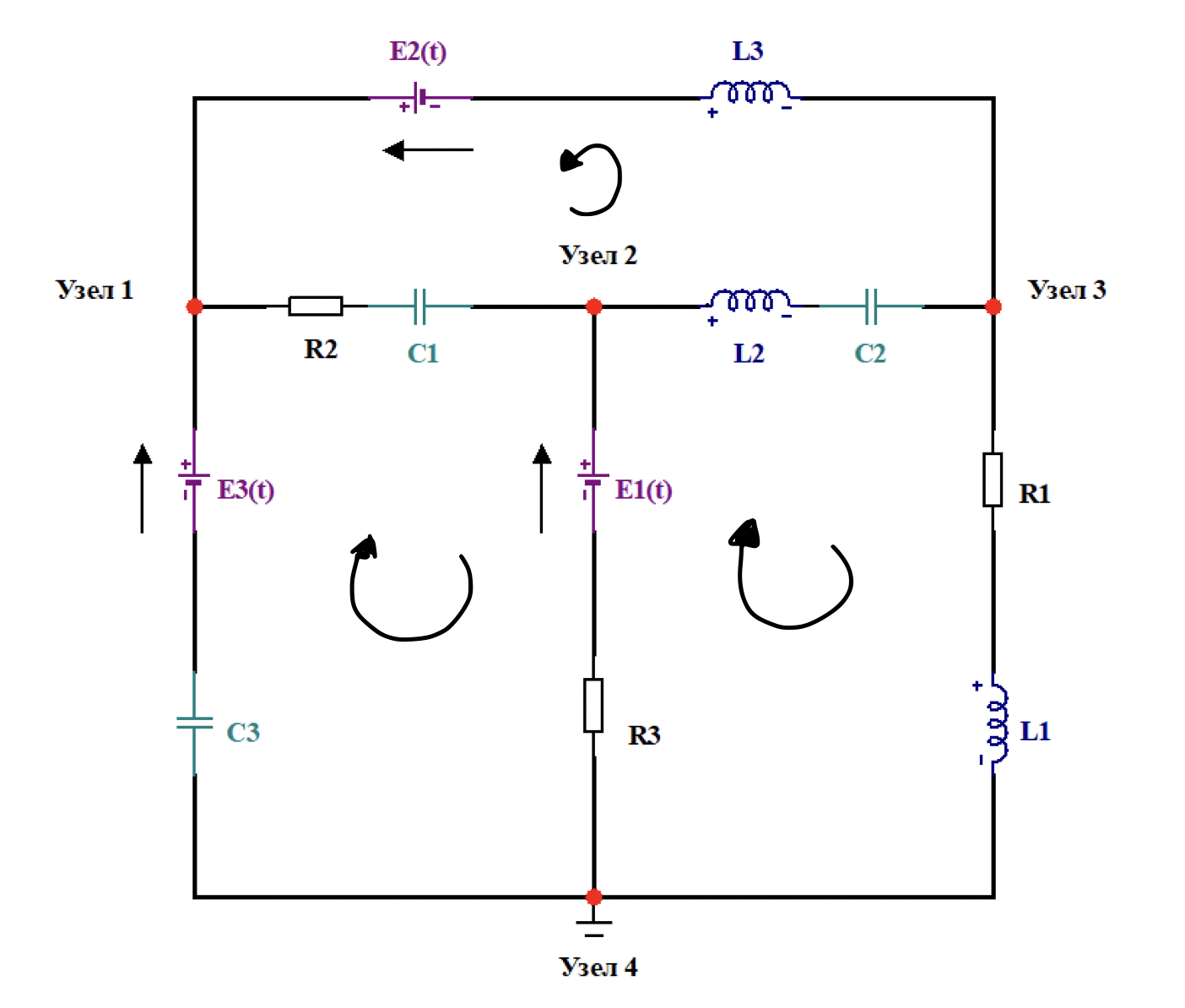
Схема 1.1.1. – Схема электрической цепи с обозначенным направлением эл. тока (с присутствующим напряжением на катушках индуктивности).
Вычисляем , :
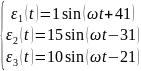
Берём t = 0, следовательно:
Составляем системы уравнений для каждого участка цепи:
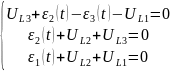
Берём t = 0, следовательно эквивалентной схеме 1.1.1. является схема 1.1.2.
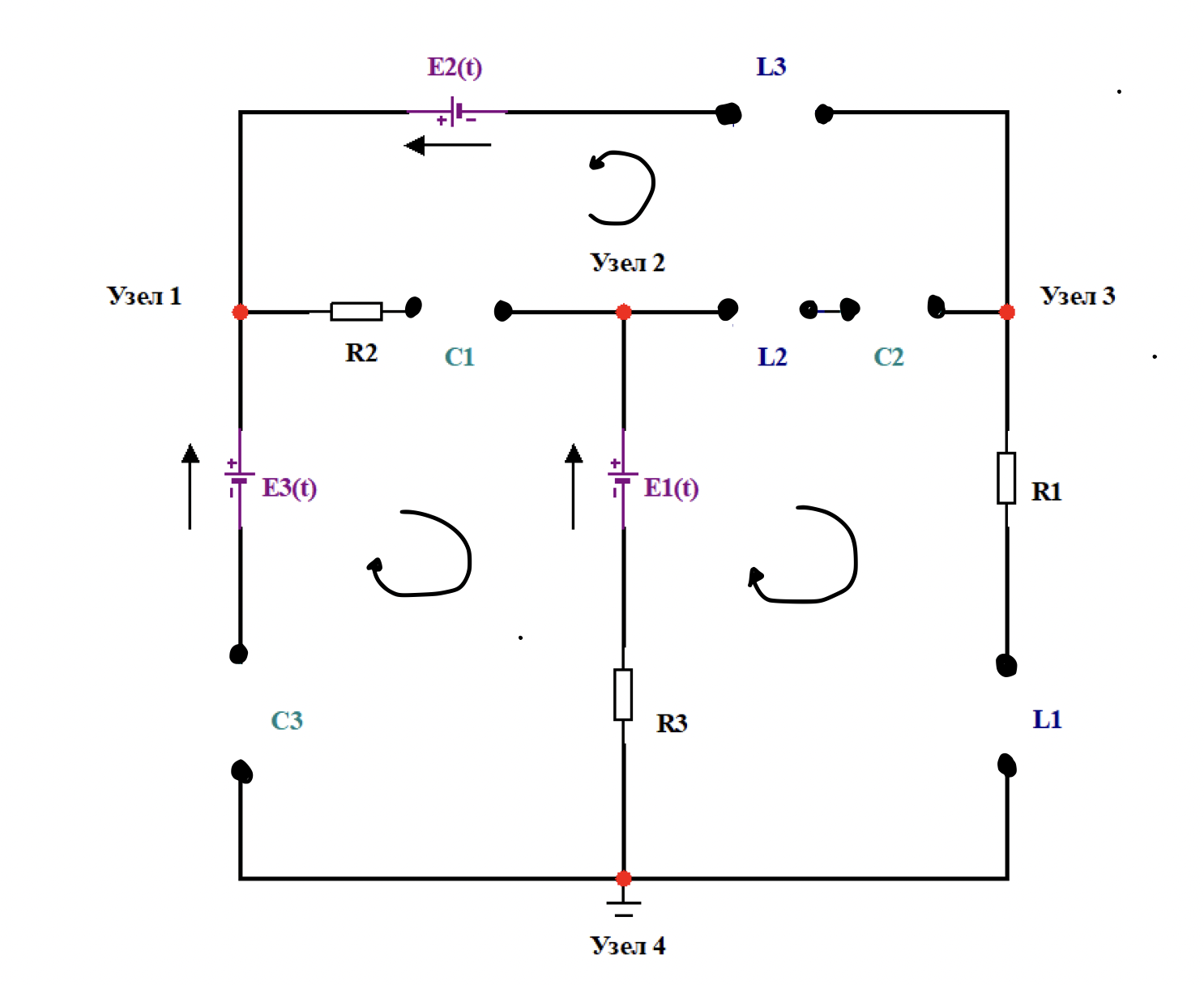
Схема 1.1.2. – Эквивалентная схема, схеме 1.1.1.
Вычисляем
,
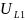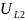и
:
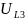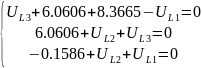
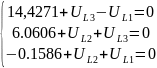
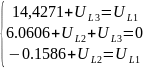
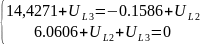
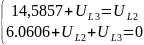
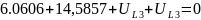
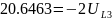
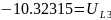
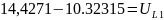
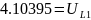
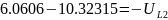
Получаем следующие
результаты:
,
,
=
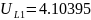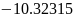
Схема электрической цепи c обозначенными направлениями эл. тока для варианта №6 представлена на схеме 1.1.3. Напряжение присутствует только на конденсаторах.
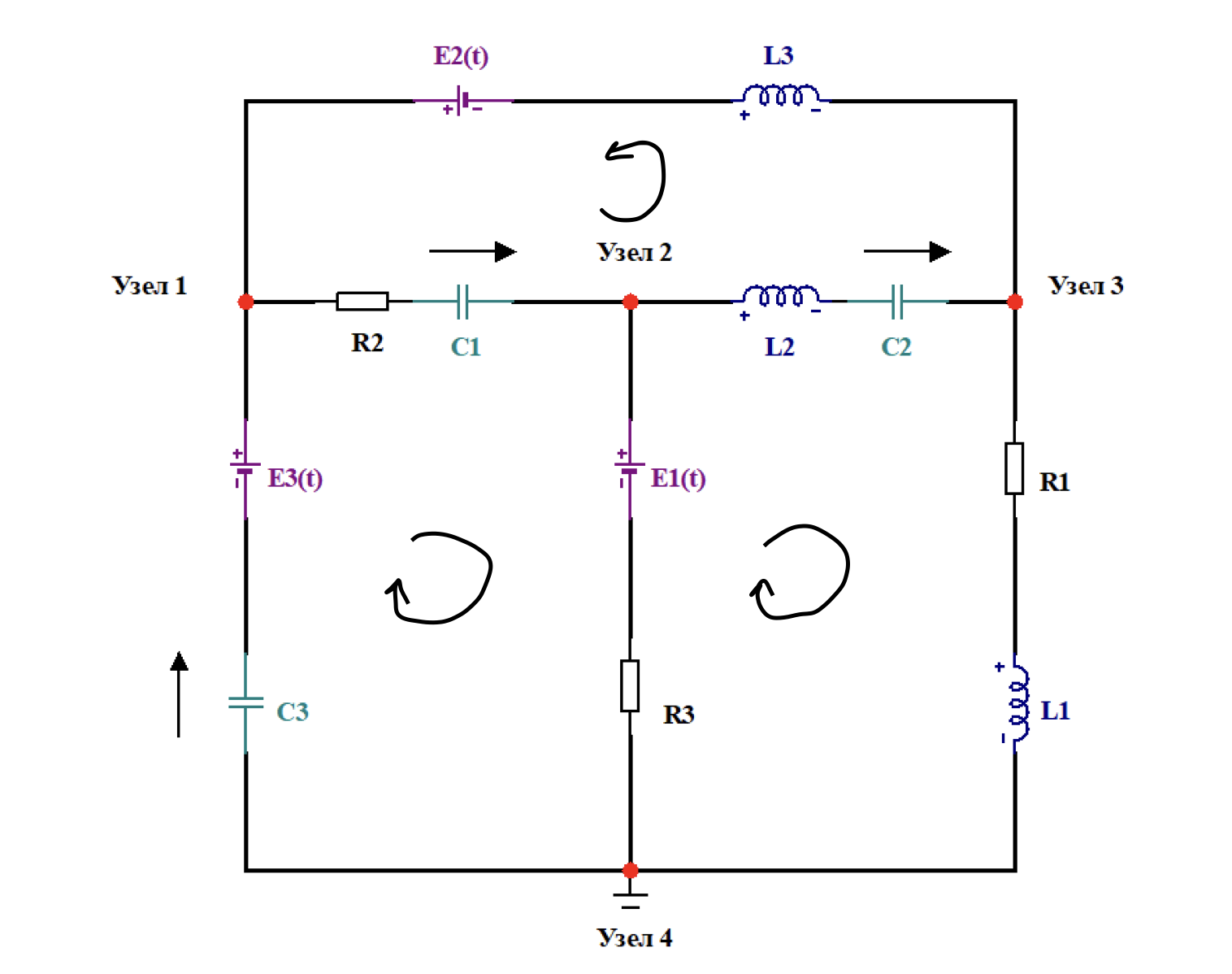
Схема 1.1.3. – Схема электрической цепи с обозначенным направлением эл. тока (с присутствующим напряжением на конденсаторах).
Берём t → ∞, следовательно эквивалентной схеме 1.1.3 является схема 1.1.4
Схема 1.1.4. – Эквивалентная схема, схеме 1.1.3.
Вычисляем
,
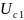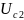и
:
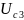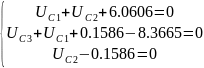
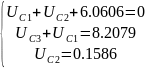
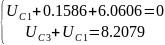
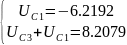
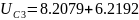
Получаем следующие
результаты:
,
,
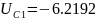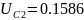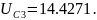
Токи всех ветвей
равны нулю:
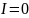Ампер. Напряжение
на катушках индуктивности равны нулю:
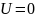Вольт. Исходя
из написанного выше, сделаем вывод, что
при постоянном токе цепь имеет резистивный
характер.
1.2. Анализ цепи при гармонических функциях источника в комплексной области
а) Привести схему электрической цепи во временной области;
б) Составить необходимое и достаточное число уравнений цепи, применяя метод уравнений Кирхгоффа;
в) Составить необходимое и достаточное число уравнений, применяя метод контурных токов;
г) Составить матрицы коэффициентов и правых частей уравнения.
Схема электрической
цепи во временной области для варианта
№6 c
обозначенными направлениями тока
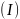представлена на схеме 1.2.1.
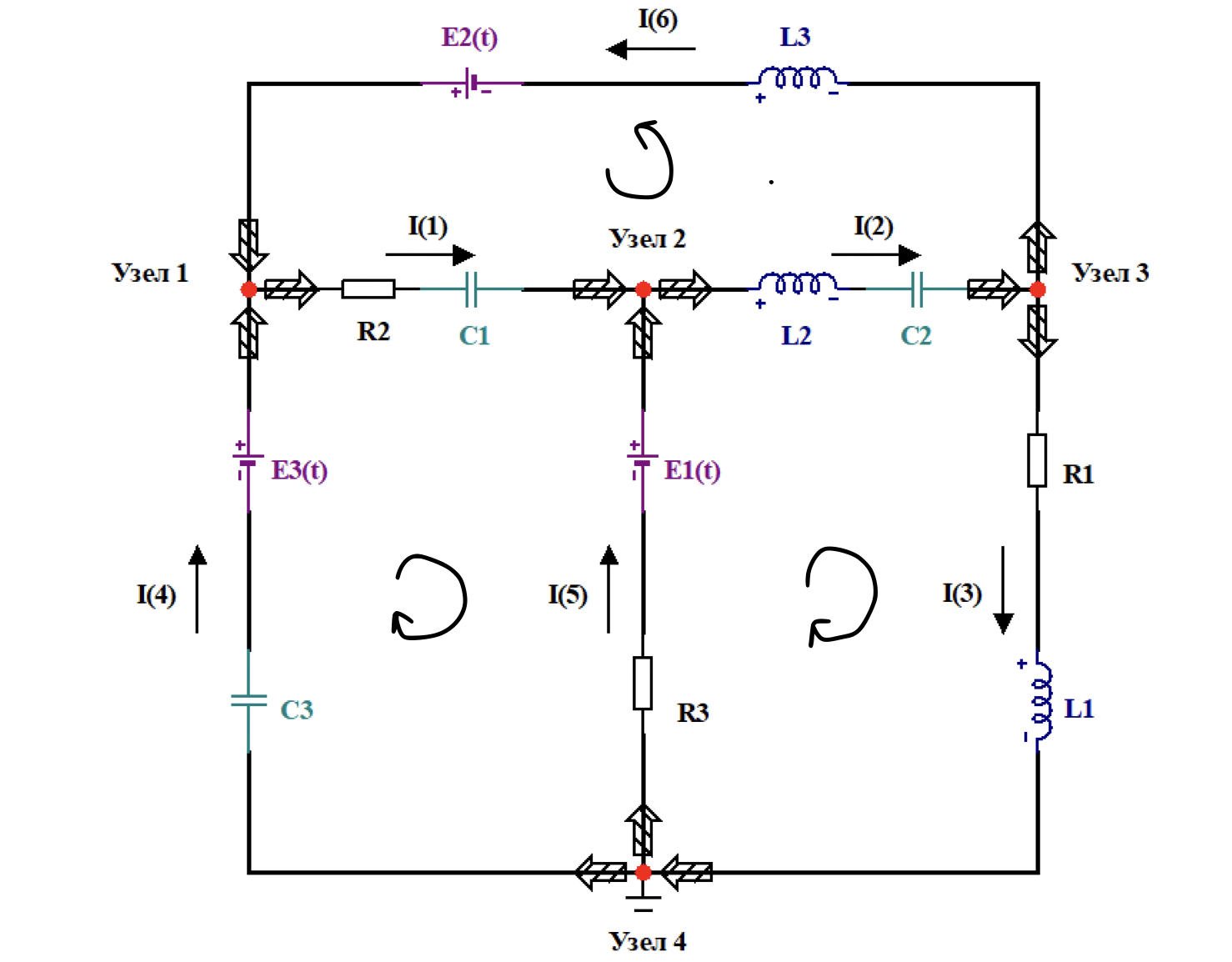
Схема 1.2.1. – Схема электрической цепи во временной области.
По каждой ветви проходит свой ток, следовательно, число неизвестных токов равно числу ветвей, и для определения токов необходимо составить 6 уравнений. Расписываем по 1-ому закону Кирхгоффа уравнения для узлов 1, 2 и 3:
Уравнение
для первого узла:
;
Для
второго узла:
;
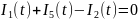И
для третьего:
.
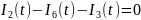Для независимых контуров п о 2-му закону Кирхгофа получаем недостающее количество уравнений:
Для 1-ого контура:
;
;
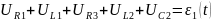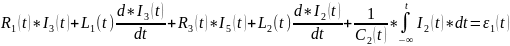Для 2-ого контура:
;
;
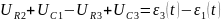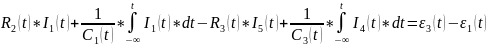Для 3-его контура:
;
.
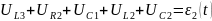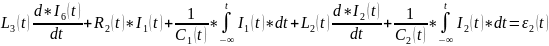Система уравнений по методу контурных токов. Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании 2-го закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.
На
схеме 1.2.2 изображены общие токи контура
.
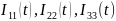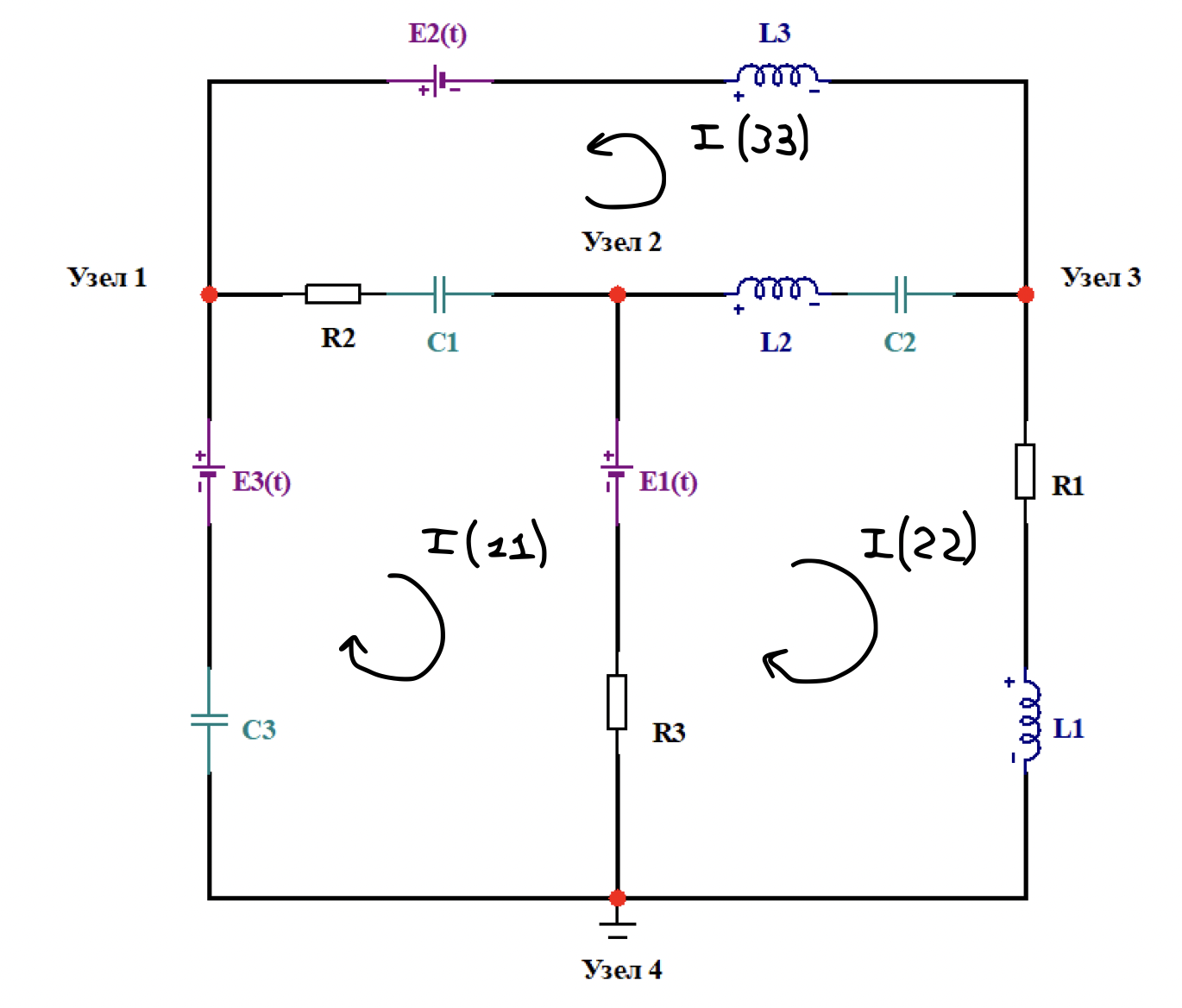
Схема 1.2.2. – Схема электрической цепи во временной области c общими токами .
Упрощаем формулы, приводя общие токи:
Для 1-ого контура:
;
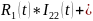Для 2-ого контура:
;
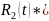Для 3-его контура:
.
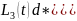Судя из законов Кирхгоффа:
а)
Получаем следующую матрицу сопротивлений
A1
(каждый
столбец сопутствует значению
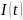от 1-ого до 6-го соответственно из
неупрощённых формул для каждых из трёх
контуров):
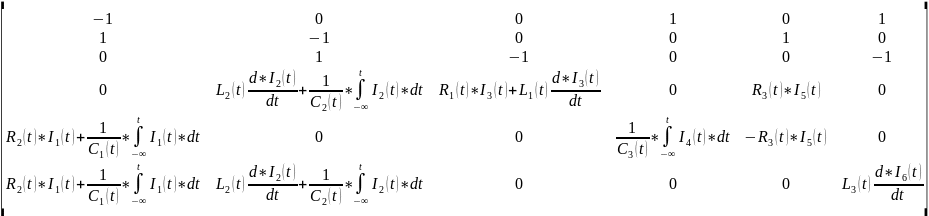
б) Матрица правой части уравнений B1 (каждая строка сопутствует значению каждых из трёх контуров):
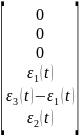
Судя из метода контурных токов:
а) Получаем следующую матрицу сопротивлений A2 (каждый столбец сопутствует значению , соответственно из упрощённых формул для каждых из трёх контуров):
б) Матрица правой части уравнений B2 (каждая строка сопутствует значению каждых из трёх контуров):
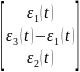
Решение
для токов проводятся по формуле
