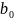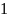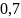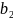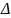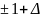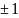МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ

КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра «Общей Теории Связи»

Лабораторная работа №1

«Анализ Нерекурсивных Цифровых Фильтров 1-го и 2-го порядка»

по дисциплине

«Цифровая обработка сигналов»

Выполнили студенты гр. XXXX:

https://t.me/mattervisualizer.

Проверил:

Москва, 2023 г.

СОДЕРЖАНИ

1. ЦЕЛЬ РАБОТЫ: 2

1.2 ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ 2

2. ВЫПОЛНЕНИЕ 3

4. ВЫВОД: 20

4.1 Анализ устойчивости 20

4.2 Классификация фильтров 20

4.3 Анализ поведения АЧХ 20

4.4 Недостатки и преимущества исследуемых фильтров 20

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ: 22

1. ЦЕЛЬ РАБОТЫ: 2

1.2 ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ 2

2. ВЫПОЛНЕНИЕ 3

3. ЛАБОРАТОРНОЕ ЗАДАНИЕ 8

4. ВЫВОД: 19

4.1 Анализ устойчивости 19

4.2 Классификация фильтров 19

4.3 Анализ поведения АЧХ 19

4.4 Недостатки и преимущества исследуемых фильтров 19

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ: 21

1. ЦЕЛЬ РАБОТЫ:

На персональном компьютере провести экспериментальный анализ нерекрусивных (трансверсальных) фильтров (ЦФ) первого и второго порядков. Исследовать частотные и временные характеристики фильтров, а также их взаимосвязь со значениями коэффициентов (параметров) ЦФ.

2. ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ

Исходные данные варианта № 22 представлены в таблице 1.

Таблица 1 – Значения параметров фильтра.

2. ВЫПОЛНЕНИЕ

Разностное уравнение нерекрусивного ЦФ первого порядка имеет вид:

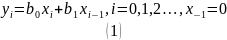
Фильтр является фильтром первого порядка, поскольку максимальный коэффициент параметра .

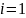Структурная схема нерекурсивного ЦФ первого порядка представлена на рисунке 1.

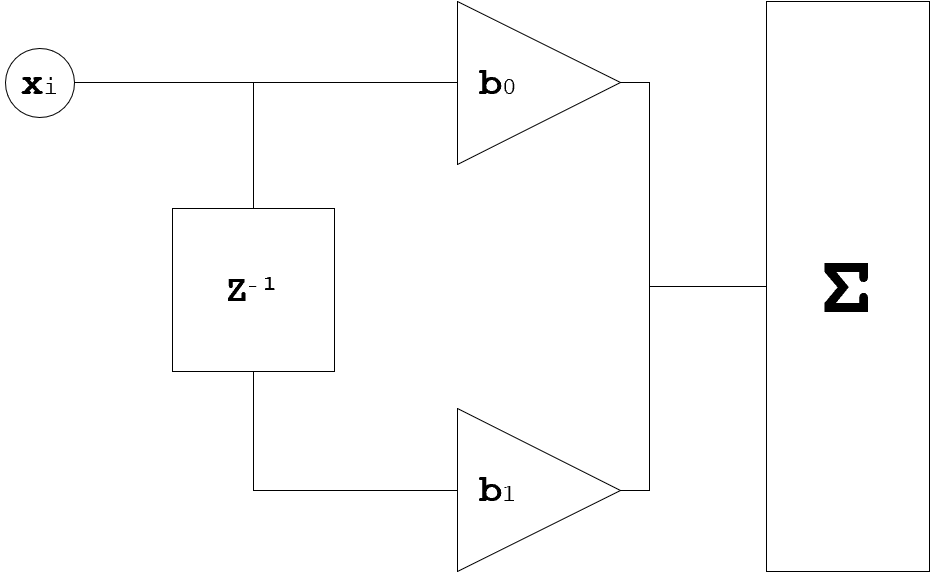
Рисунок 1 – Структурная схема нерекрусивного ЦФ первого порядка

Системной функцией ЦФ назвается следующее отношения:

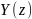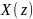Обе части ( и ) можно представить так, с использованием Z-Преобразований:

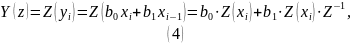
Следовательно:

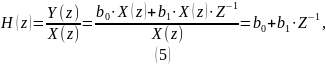
Подставив значения получаем:

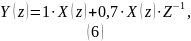
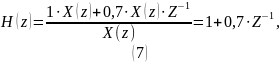
Импульсная и переходная характеристики (ИХ и ПХ) выражаются следующим образом, где ­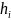– ИХ, а 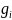– ПХ.

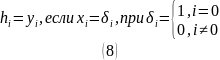
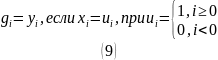
Выражая получаем:

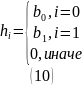
Поскольку:

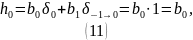
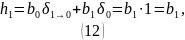
Подставив значения получаем:

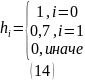
График ИХ представлен на рисунке 2.

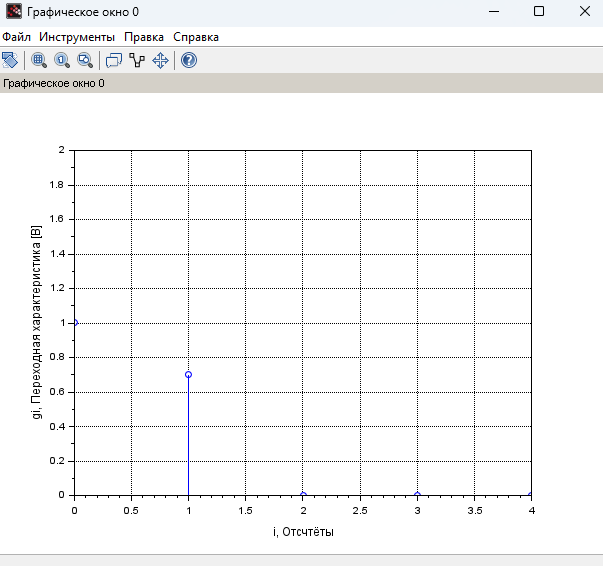
Рисунок 2 – График ИХ (импульсной характеристики)

Выражая получаем:

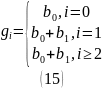
Поскольку:

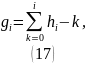
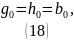
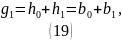
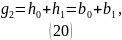
Подставив значения получаем:

График ПХ представлен на рисунке 3.

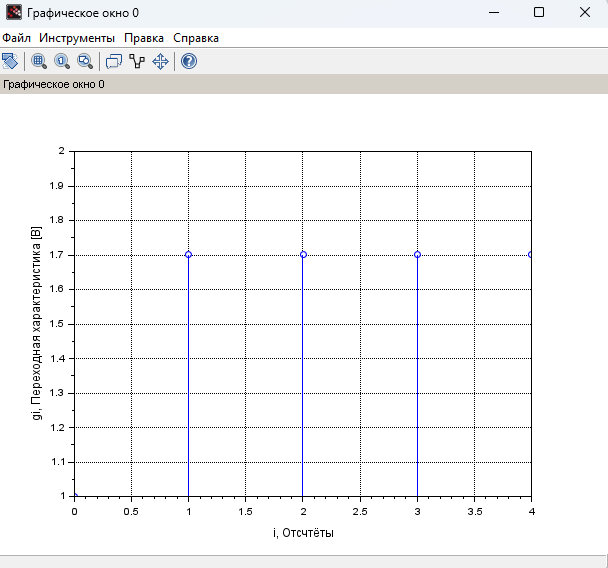
Рисунок 3 – График ПХ (переходной характеристики)

Расчёт АЧХ и ФЧХ производится с помощью ранее найденной системной функции ЦФ. Заменив в ней параметр 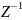получаем:

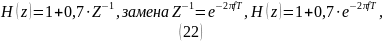
По формуле Эйлера:

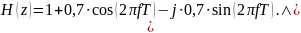
Выделив действительную и мнимую часть, получаем:

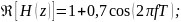
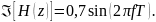
Следуя из всего написанного выше, формула АЧХ:

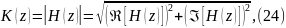
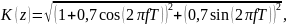
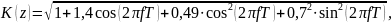
А формула ФЧХ:

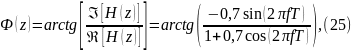
График ФЧХ представлен на рисунке 4.

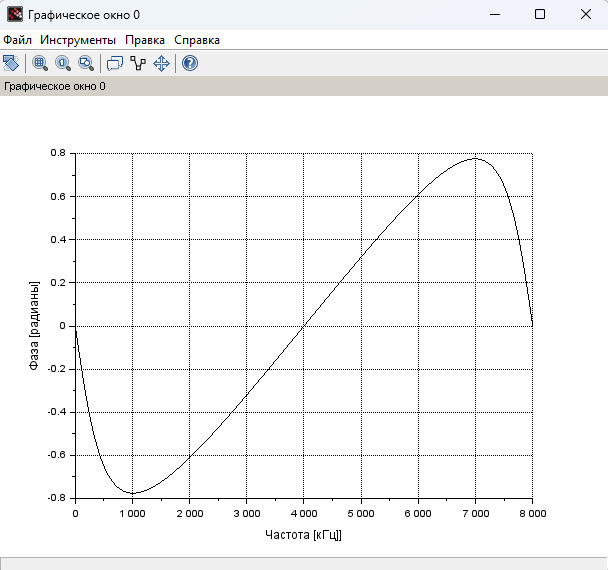
Рисунок 4 – ФЧХ

График АЧХ представлен на рисунке 5.

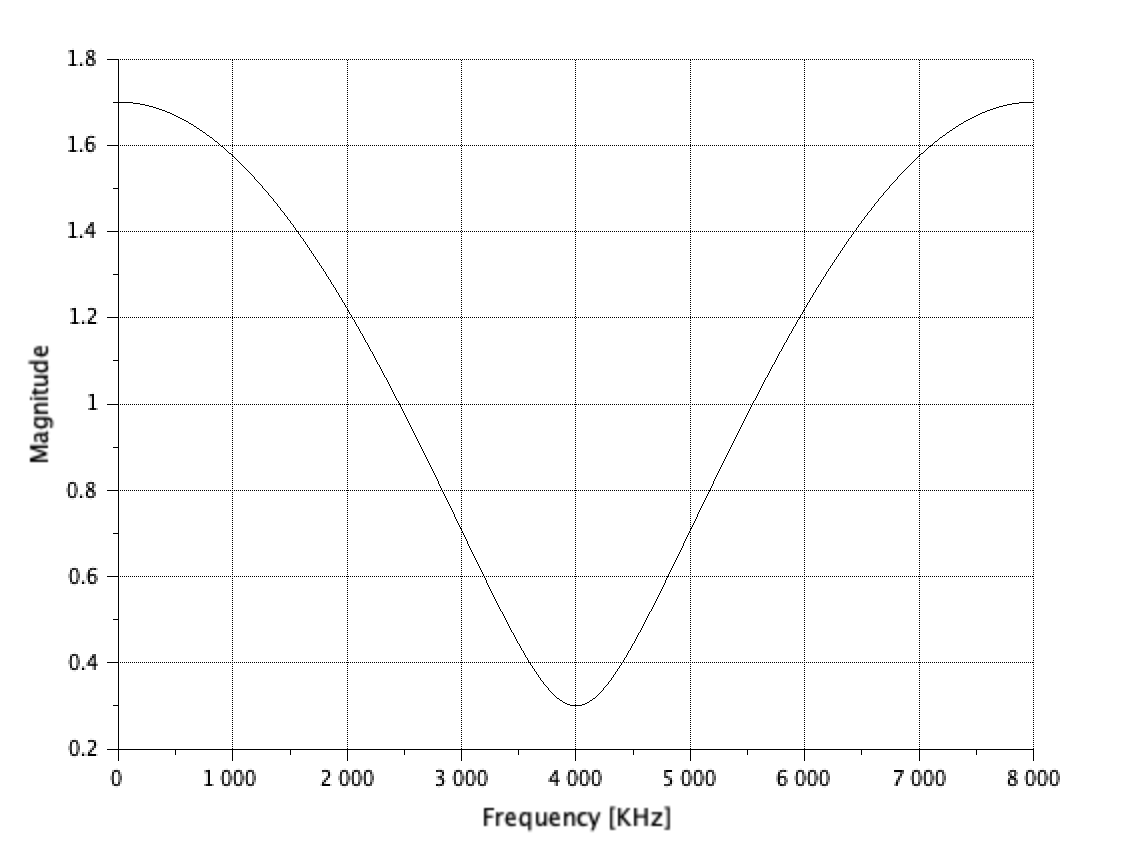
Рисунок 5 – АЧХ

3. ЛАБОРАТОРНОЕ ЗАДАНИЕ

Значения коэффициентов для нерекурсивного ЦФ первого порядка представлены в таблице 2. Значения коэффициентов для нерекурсивного ЦФ второго порядка представлены в таблице 3.

Таблица 2 – Значения параметров ЦФ первого порядка.

Таблица 3 – Значения параметров ЦФ второго порядка.

По аналогии с выполнением домашнего задания было записано разностное уравнение для ЦФ второго порядка:

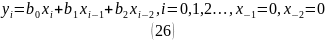
Разностное уравнение ЦФ первого порядка определяется по формуле (1).

Структурная схема нерекурсивного ЦФ второго порядка представлена на рисунке 6.

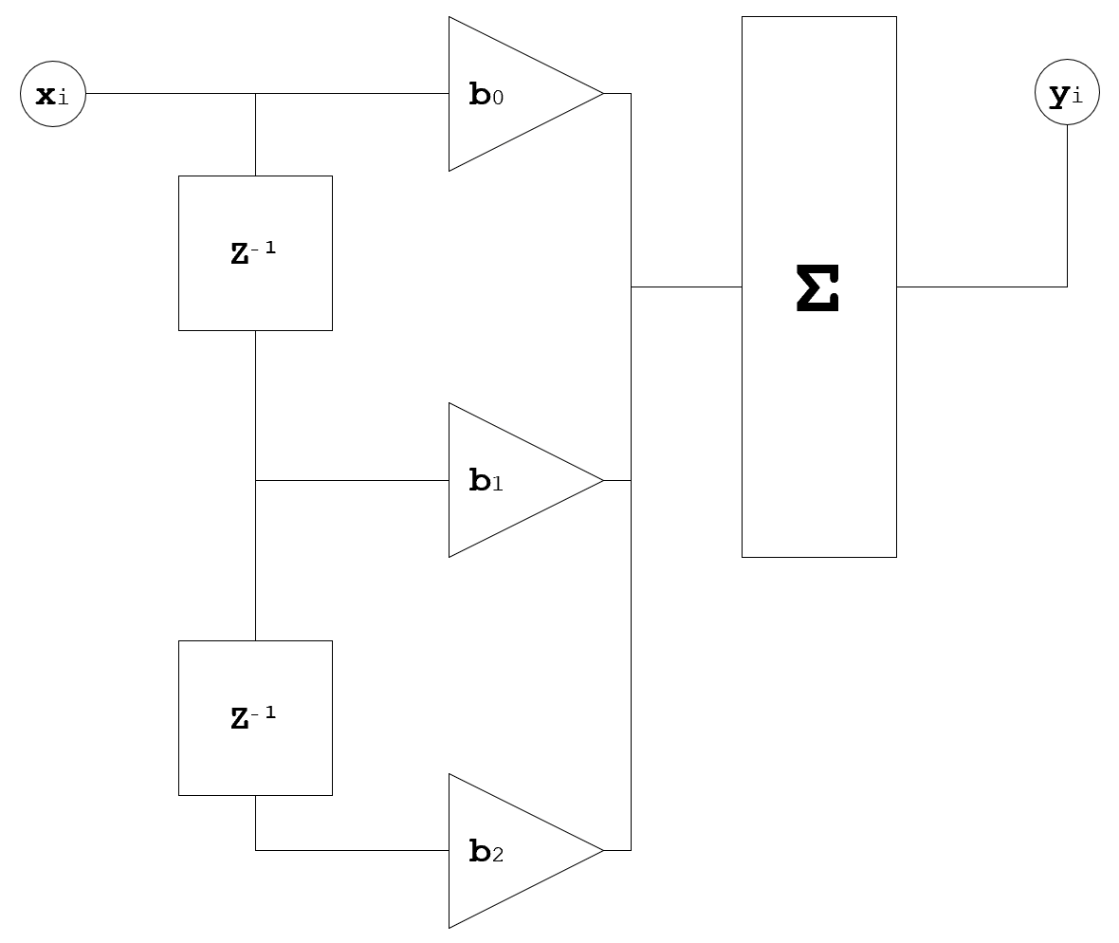
Рисунок 6 – Структурная схема нерекрусивного ЦФ второго порядка

Структурная схема нерекрусивного ЦФ первого порядка представлена ранее на рисунке 1.

Системной функцией ЦФ называется следующее отношения:

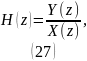
Обе части ( и ) можно представить так, с использованием Z-Преобразований:

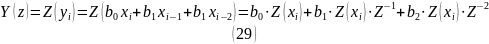
Следовательно:

Расчёт АЧХ и ФЧХ производится с помощью ранее найденной системной функции ЦФ. Заменив в ней параметр и 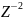получаем:

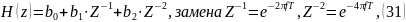
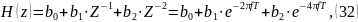
По формуле Эйлера:

Выделив действительную и мнимую часть, получаем:

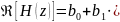
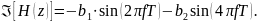
Следуя из всего написанного выше, формула АЧХ:

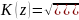
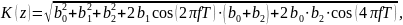
А формула ФЧХ:

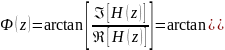
Графики АЧХ и ФЧХ при разных значениях представлены ниже на рисунках от 7 до ..

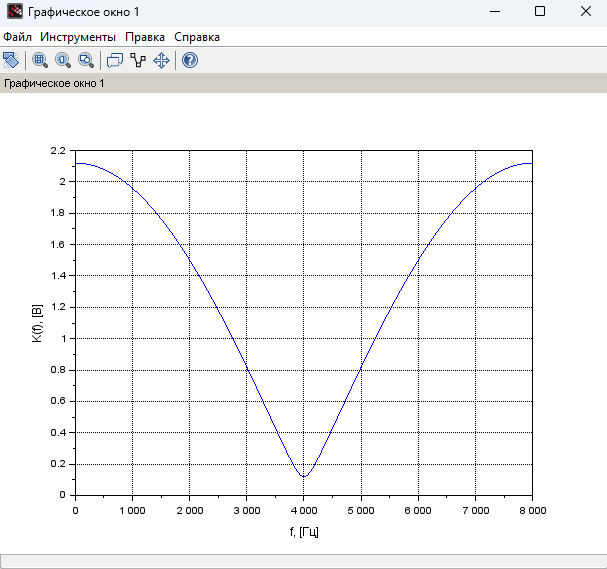
Рисунок 7 – График АЧХ при

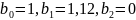
Рисунок 8 – График ФЧХ при

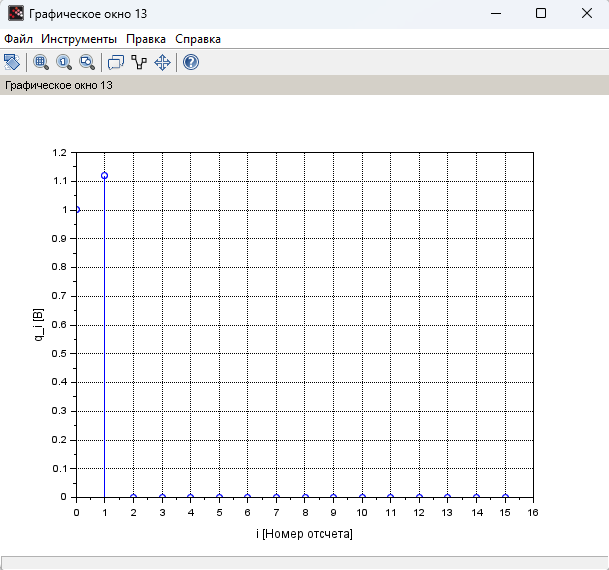
Рисунок 9 – График ИХ при

Рисунок 10 – График АЧХ при

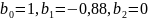
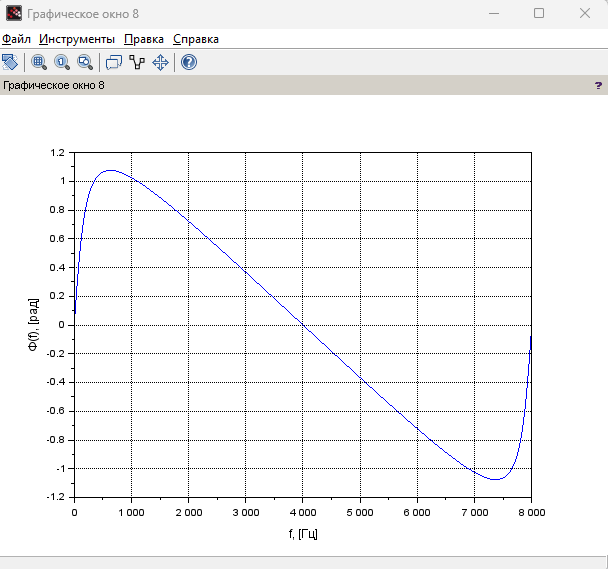
Рисунок 11 – График ФЧХ при

Рисунок 12 – График ИХ при

Рисунок 13 – График АЧХ при

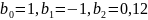
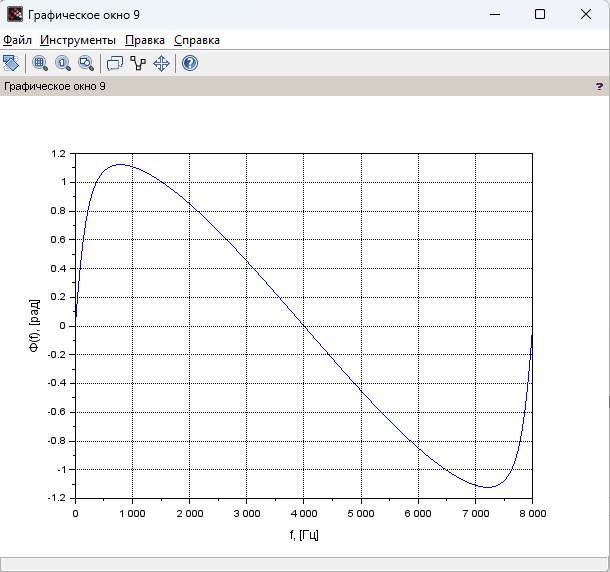
Рисунок 14 – График ФЧХ при

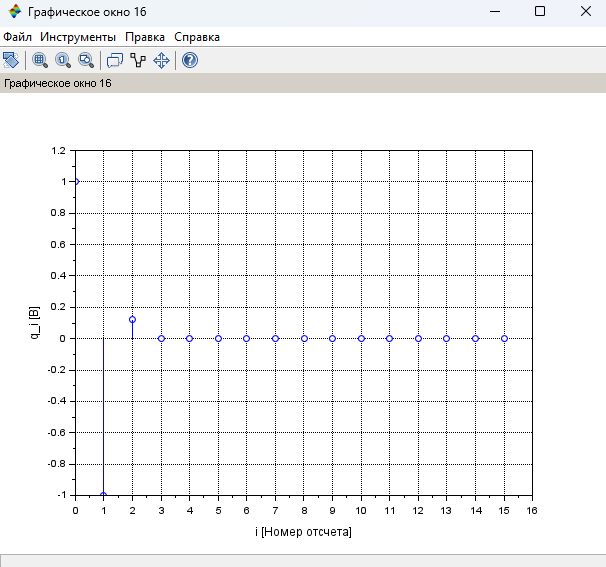
Рисунок 15 – График ИХ при

Рисунок 16 – График АЧХ при

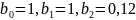
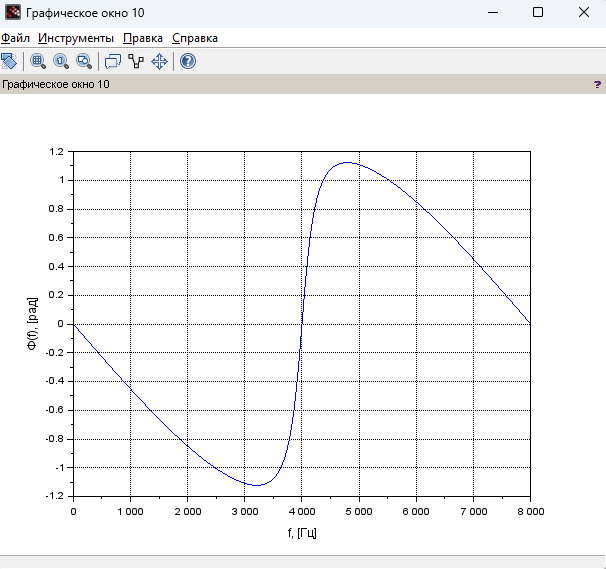
Рисунок 17 – График ФЧХ при

Рисунок 18 – График ИХ при

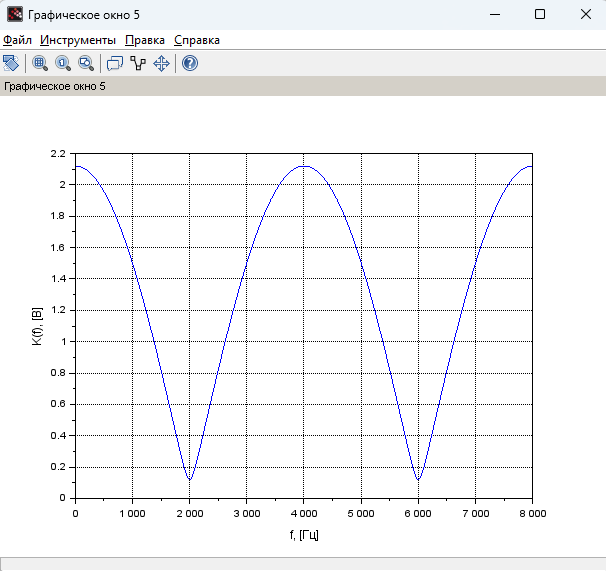
Рисунок 19 – График АЧХ при

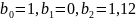
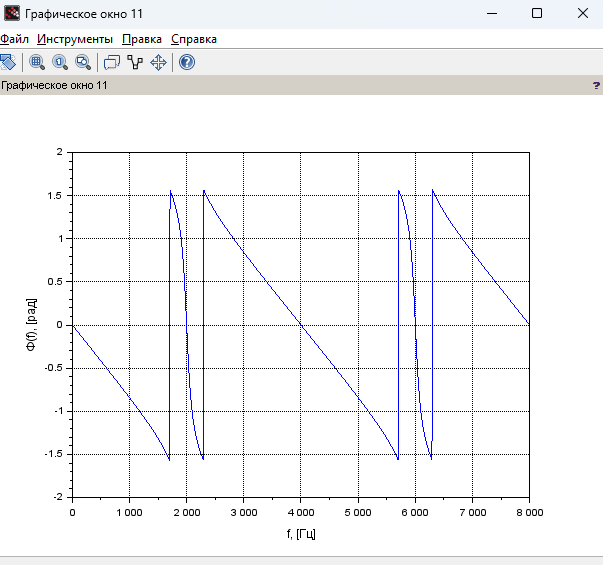
Рисунок 20 – График ФЧХ при

Рисунок 21 – График ИХ при

Рисунок 22 – График АЧХ при

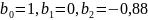
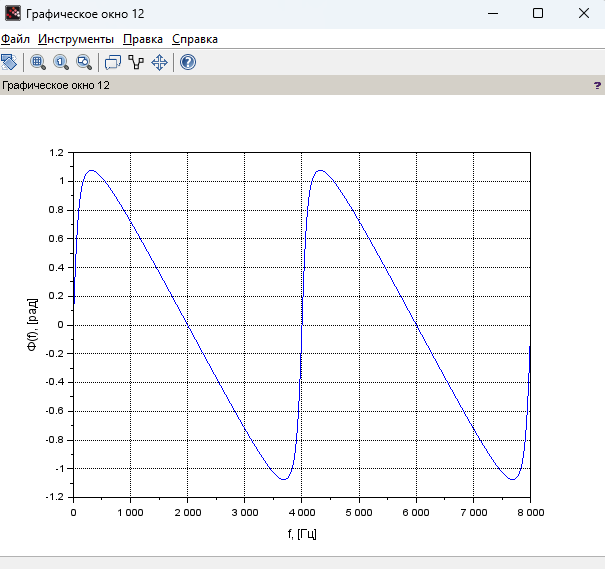
Рисунок 23 – График ФЧХ при

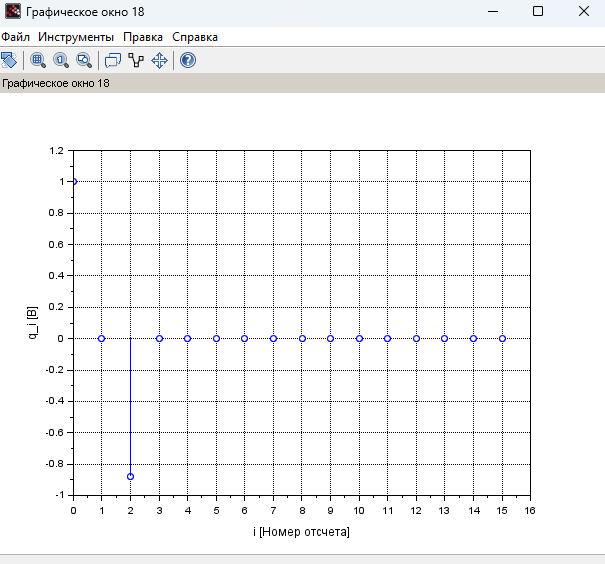
Рисунок 24 – График ИХ при

4. ВЫВОД:

4.1 Анализ устойчивости

Нерекурсивные фильтры являются устойчивыми, так как при любых начальных условиях реакция фильтра на любое ограниченное воздействие также ограничена (имеет конечную импульсную характеристику).

4.2 Классификация фильтров

Вид фильтра определяется по характеру локализации АЧХ в частотной области. У фильтров нижних частот (ФНЧ) локализация АЧХ происходит у нулевой частоты, в то время, как у фильтров верхних частот (ФВЧ) локализация у частоты Найквиста.

Фильтры, полученные в результате выполнения лабораторной работы:

Фильтр №1: (b0=1; b1=1,12;b2=0 ). 1 ФНЧ

Фильтр №2: (b0=1; b1=-0,88;b2=0 ). 1 ФВЧ

Фильтр №3: (b0=1; b1=-1;b2=0,12). 2 ФВЧ

Фильтр №4: (b0=1; b1=1;b2=0,12). 2 ФНЧ

Фильтр №5: (b0=1; b1=0;b2=1,12). 1 рф

Фильтр №6: (b0=1; b1=0;b2=-0,88). 1 пф

4.3 Анализ поведения АЧХ

Нерекурсивные ЦФ 1-го порядка имеют меньшую крутизну АЧХ, чем нерекурсивные ЦФ 2-го порядка. У ФВЧ 1-го порядка крутизна АЧХ (фильтр №2) меньше чем у ФВЧ 2-го порядка (фильтр №6). ФВЧ 2-го порядка обладает пульсацией вне полосы пропускания (фильтр №5), а также в полосе пропускания (фильтр №7). Нерекурсивные ФНЧ 1-го порядка недостаточно подавляют высокие частоты (фильтр №1), ФНЧ 2-го порядка имеет пульсации вне полосы пропускания (фильтр №3), а также в полосе пропускания (фильтр №4).

4.4 Недостатки и преимущества исследуемых фильтров

Преимущества:

Основными преимуществами нерекурсивного фильтра является простота анализа и реализации, а также наглядная связь коэффициентов фильтра с отсчетами его импульсной характеристики и абсолютная устойчивость.

Недостатки:

Несмотря на то, что длительность импульсной характеристики нерекурсивного фильтра конечна, она может оказаться достаточно большой для достижения резкого спада частотной характеристики на границе зоны пропускания, также для получения приемлемых частотных характеристик (например, полосовых фильтров с высокой прямоугольностью АЧХ) необходимы нерекурсивные фильтры высокого порядка до нескольких сотен и даже тысяч.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ:

1) Санников В.Г. и др. Лабораторная работа № 26 Анализ и эмпирический синтез цифровых фильтров, М.: 2009

2) Задание к лабораторной работе 26- 1. Электронный файл – Задание_lab26-1_2022.pdf (высылается преподавателем через старосту группы)

3) Правила электронной верстки отчетов по лабораторному практикуму. Электронный файл – Правила электронной верстки лаб. отчетов по ЦОС_06_09_2022.pdf

4) Электронный файл – Варианты заданий для лаб.26-1_2022.

Дополнительные материалы

5) А.Б. Сергиенко. Цифровая обработка сигналов (Учебник для вузов, 2-е издание) – СПб.: Изд. «Питер», 2007. (возможны более ранние и более поздние издания).

6) Юрий Лазарев. MatLAB 5.x (серия «Библиотека студента»), Киев: Издательская группа BHV, 2000.

7) В. Г. Потемкин. Система инженерных и научных расчетов MATLAB 5.x, Том.1, Москва: «Диалог-МИФИ, 1999.