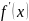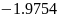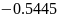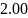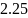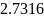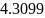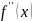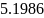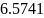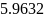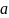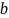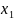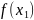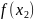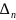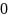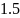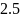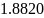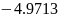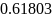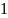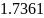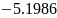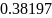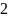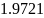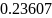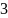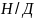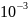ЛР-0006 (Одномерная оптимизация) / chm_lab_0006_final
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И
МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский Технический Университет Связи и Информатики»
Кафедра «Информатика»
Лабораторная работа №6
«Одномерная оптимизация»
по дисциплине
«Численные методы»
Выполнил студент гр. XXXX:
https://t.me/mattervisualizer
Проверил:
Москва, 2023 г.
Содержание.
Индивидуальное задание.
В данной лабораторной работе необходимо
выполнить задачу одномерной оптимизации
по заданным данным: функции
,
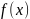минимум которой необходимо найти и
методу. В варианте 6 используется метод
золотого сечения в качестве ручного
расчёта и оценить её погрешность. Для
метода дихотомии необходимо написать
программный код, вычисляющий координаты
точки минимума функции и получить
результаты с точностью
.
Также необходимо провести исследование
функции
.
Заданная функция
в варианте
.
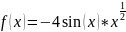Исследование функции.
График функции и двух её производных представлен на рисунке 2.1.
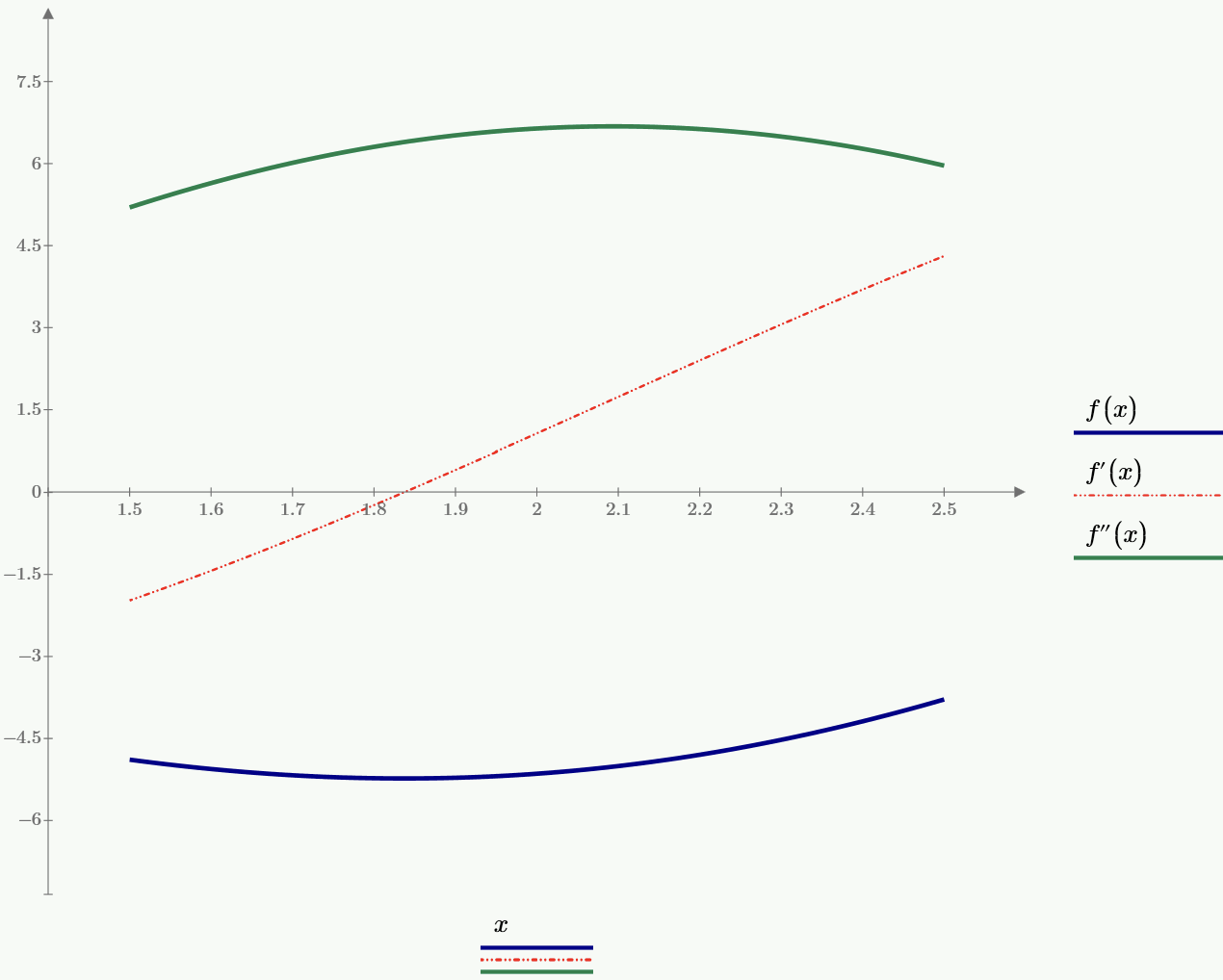
Рисунок 2.1. – График функции и её двух производных.
Аналитическому условию унимодальности
функции на выбранном отрезке
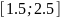выполняется, поскольку первая производная
функции
монотонно возрастает, а вторая – не
обращается в нуль, что видно по графику.
Аналитическое доказательство:
а)
,
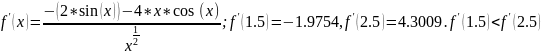см. таблицу 2.1.
б)
,
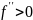см. таблицу 2.2.
Таблица 2.1. – Таблица значений
производной
Таблица 2.2. – Таблица значений
производной
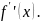
Унимодальность функции доказана. На данном промежутке существует минимум функции.
Метод золотого сечения (ручной расчёт).
Для проведения расчётов по методу золотого сечения необходимо выполнить три итерации для расчёта точки минимума функции на отрезке. Расчёты и оценка погрешности представлены в таблице 3.1.
Таблица 3.1. – Таблица расчёта минимума функции на промежутке методом золотого сечения.
Миниммум
найден в точке
.
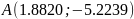Метод дихотомии (с использованием программного кода).
Программный код представлен на листинге 4.1.
#include <iostream>
#include <cmath>
double f(double x)
{
return -4*sin(x);
}
void countmepls(double& a, double& b, double& eps, double& delta)
{
do
{
double x_1 = (a + b - delta)/2;
double x_2 = (a + b + delta)/2;
if (f(x_1)>f(x_2))
{
a = x_1;
}
else
{
b = x_2;
}
}
while ((b-a) <= eps);
std::cout << "MIN(x, y) = (" << (a+b)/2 << ", " << f((a+b)/2) << ")\n";
}
int main()
{
double a, b, eps, delta;
std::cout << "[a] Введите начальную точку отрезка >> ";
std::cin >> a;
std::cout << "\n";
std::cout << "[b] Введите конечную точку отрезка >> ";
std::cin >> b;
std::cout << "\n";
std::cout << "[ε] Введите точность >> ";
std::cin >> eps;
std::cout << "\n";
std::cout << "Введите параметр метода, который соответсвует условию: d ∈ (0, b - a / 2) ";
std::cin >> delta;
std::cout << "\n";
countmepls(a, b, eps, delta);
}
Листинг 4.1. – Программный код.
Значения функции при заданных точностях показаны в таблице 4.1.
Таблица 4.1. – Значения функции при разных точностях.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод.
Был проведён анализ функции, найдены минимумы функции методом золотого сечения ручным способом и написана программа для метода дихотомии для вычисления минимума функции с заданной точностью.