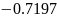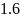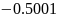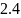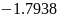МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И
МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский Технический Университет Связи и Информатики»
Кафедра «Информатика»
Лабораторная работа №5
«Методы решения обыкновенных дифференциальных уравнений»
по дисциплине
«Численные методы»
Выполнил студент гр. XXXX:
https://t.me/mattervisualizer
Проверил:
Москва, 2023 г.
Содержание.
Индивидуальное задание.
В данной лабораторной работе необходимо
решить обыкновенное уравнения вида
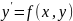c заданным интервалом
,
где
и
– начальная и конечная точка функции
,
начальными условиями
и
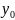и шагом интегрирования
.
Нужно найти аналитическое решение
заданного дифференциального уравнения,
полагая его точным, вычислить значения
полученного решения
,
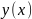найти численное решение дифференциального
уравнения методом Эйлера
в отрезке ручным счётом, вычислить
значение погрешностей
для
.
Составить схему алгоритма и написать
программу интегрирования дифференциальных
уравнений методом Рунге-Кутты 4-ого
порядка с автоматическим выбором шага
и провести контрольные тестирование
на примере. Получить решение «расчётом
на ПК»
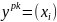с шагом
,
и
.
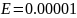Вычислить значения погрешностей
.
Графически проиллюстрировать решения
.
Решение будет производиться в
математическом пакете Mathcad
Prime 8. Программный код для
вычисления дифференциального уравнения
написан на языке программирования C++.
Данные задания варианта 6 представлены в таблице 1.1.
Таблица 1.1. – Исходные данные.
-
Уравнение
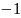
Точное аналитическое решение заданного дифференциального уравнения.
Точное аналитическое решение заданного
дифференциального уравнения варианта
6 (т. е.
найдено разделением переменных (т. е.
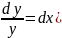и интегрированием с учётом начальных
условий. Аналитическое решение
представлено на рисунке 2.1.
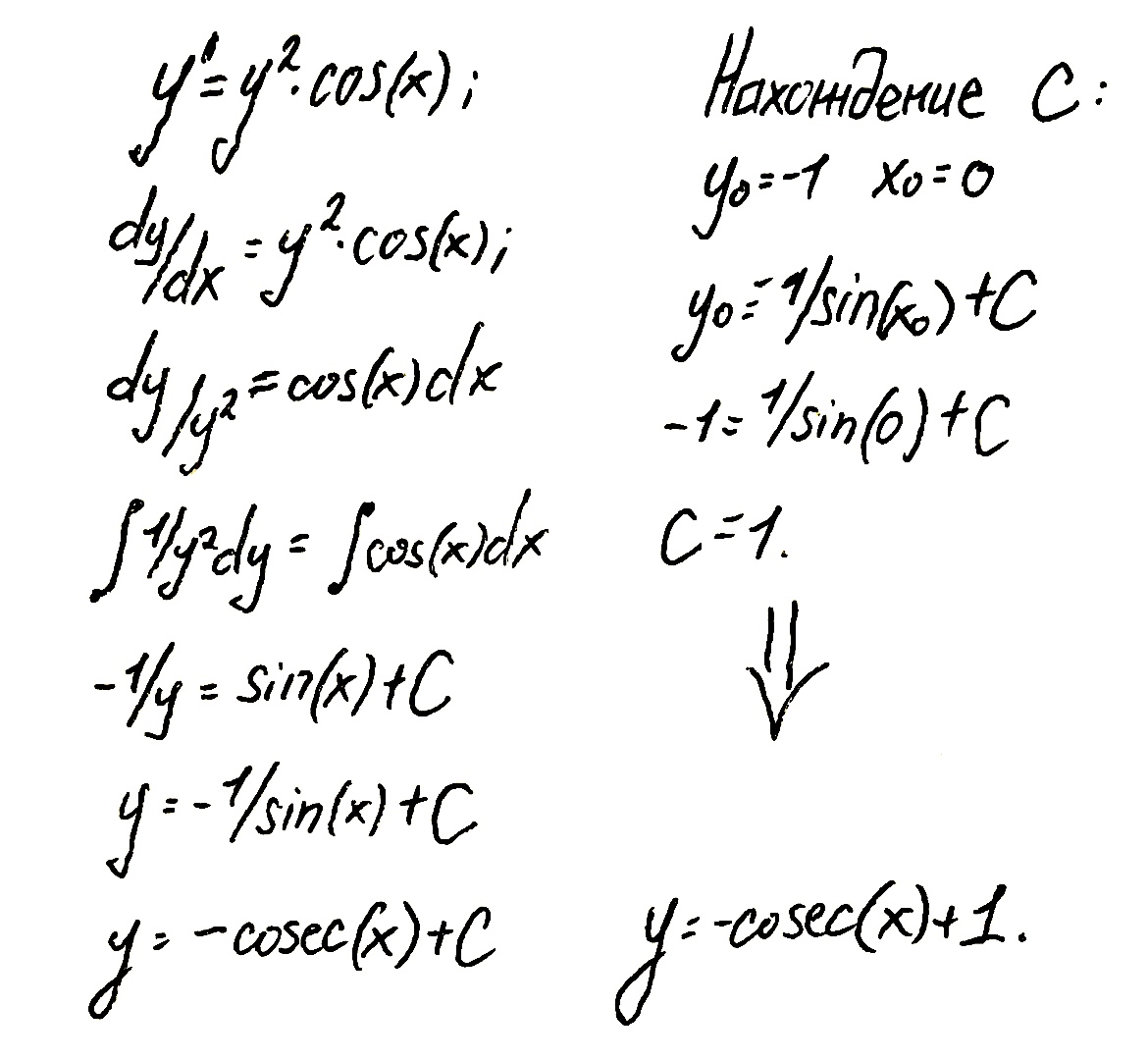
Таблица 2.1. – Аналитическое решение данного дифферециального уравнения.
Получившееся уравнение, решённое
аналитически -
.
Значение точного оду.
Вычисленные значение аналитического уравнения представлено в таблице 3.1. (с данным шагом изменения аргумента и интервалом).
Таблица 3.1. – Значения аналитического уравнения.
