МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И

МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский Технический Университет Связи и Информатики»

Кафедра «Информатика»

Лабораторная работа №4

«Численное интегрирование.»

по дисциплине

«Численные методы»

Выполнил студент гр. XXXX:

https://t.me/mattervisualizer

Проверил:

Москва, 2023 г.

Содержание.

1. Индивидуальное задание.

В данной лабораторной работе необходимо выполнить численное интегрирование подынтегральной функции в пределах от до , используя методы (метод Симпсона) и (метод трапеций). Для метода трапеций необходимо определять значения с шагом и . Для метода Симпсона необходимо написать программу с точностями . Провести оценку погрешности полученных результатов по правилу Рунге. Построить график зависимости числа разбиений отрезка от заданной точности.

2. Численное интегрирование по методу Симпсона.

Для численного интегрирования по методу Симпсона был использован математический пакет Mathcad Prime 8. Перенесённые данные в программу показаны (для шага ) на рисунке 2.1, для шага на рисунке 2.2. Все данные перенесены в таблицу 2.1.

Рисунок 2.1. – Перенесённые данные для .

Рисунок 2.2. – Перенесённые данные для .

Таблица 2.1. – Значения функции.

Интегралы были вычислены два раза: для шага и . Вычисления для соответствующих шагов показаны на рисунках 2.3 и 2.4. Значения интегралов для каждого из вычислений занесены в таблицу 2.2.

Рисунок 2.3. – Вычисление интеграла функции для .

Рисунок 2.4. – Вычисление интеграла функции для .

Таблица 2.2. – Значения интегралов.

	Значение вычисленного интеграла

Была произведена оценка погрешности по правилу Рунга. Она составила . В предыдущих лабораторных работах была обозначена планка в максимально допустимую погрешность в , поэтому здесь была взята она же. Число, получившееся в результате оценки погрешности по правилу Рунга получилось не больше установленной погрешности, что свидетельствует о правильности расчётов (см. рисунок 2.5)

Рисунок 2.5. – Оценка погрешности по правилу Рунге.

Для численного интегрирования по методу Симпсона была написана программа на языке C++. Её программный код показан на листинге 2.1.

#include <iostream>

#include <cmath>

static double f(const double& x)

{

return 8 * sin(2 * x) - 2;

}

static double simpson_counter(const double& a, const double& b, const double& h)

{

double n = (b - a) / h, intermediateFirst = 0, intermediateSecond = 0;

for (int i = 1; i <= h / 2; i++) {

if (i > 1)

{

intermediateSecond += f(a + n * (2 * i - 1));

intermediateFirst += f(a + n * (2 * i - 2));

}

else

{

intermediateSecond += f(a + n * (2 * i - 1));

}

}

return (n / 3) * (f(a) + f(b) + 4 * intermediateSecond + 2 * intermediateFirst);

}

int main(int args, char* argv[])

{

static double a, b, e;

std::cout << "[a] Введите нижнюю границу: ";

std::cin >> a;

std::cout << "[b] Введите верхнюю границу: ";

std::cin >> b;

static double h;

std::cout << "[h] Задайте количество отрезков: ";

std::cin >> h;

std::cout << "[e] Задайте точность: ";

std::cin >> e;

static double counted_integral, counted_integral2, uncertainty;

do

{

counted_integral = simpson_counter(a, b, h);

h = h*2;

counted_integral2 = simpson_counter(a, b, h);

uncertainty = (counted_integral-counted_integral2)/15;

}

while (fabs(uncertainty) > e);

std::cout << "\n\n\n===---------------------------------------------------===\n";

std::cout << "[∫] Расчёт завершён! Получившееся значение: " << counted_integral2 + uncertainty << "\n";

std::cout << "Используемые значения: [a = " << a << "]" << " [b = " << b << "]\n";

std::cout << "Точность: " << e << "\n";

std::cout << "Оценка погрешности по Рунге: " << uncertainty << "\n";

std::cout << "===---------------------------------------------------===\n\n\n";

return 0;

}

}

}

Листинг 2.1. – Программный код.

Данная программа численно интегрирует функцию по методу Симпсона с заданным шагом и точностью. Пример её работы представлен на рисунке 2.6.

Рисунок 2.6. – Результат работы программы.

Программный и ручной расчёт совпадает, что свидетельствует о правильности работы программы. Ниже, в таблице 2.3, представлены значения интеграла функции для расчётов с указанными точностями .

Таблица 2.3. – Значения интегралов при заданных точностях, полученные с помощью программного расчёта.

	Значения интеграла	h	h/2	Оценка погрешности по Рунге

На рисунке 2.7 показан график зависимости числа разбиений от заданной точности.

Рисунок 2.7. – График зависимости числа разбиений от заданной точности.

3. Численное интегрирование по методу трапеции.

Для численного интегрирования по методу трапеции был использован математический пакет Mathcad Prime 8. Перенесённые данные в программу показаны на рисунке 3.1. Все данные перенесены в таблицу 3.1.

Рисунок 3.1. – Перенесённые данные.

Таблица 3.1. – Значения функции.

Интегралы были вычислены два раза: для шага и . Вычисления для соответствующих шагов показаны на рисунке 3.2. Значения интегралов для каждого из вычислений занесены в таблицу 3.2.

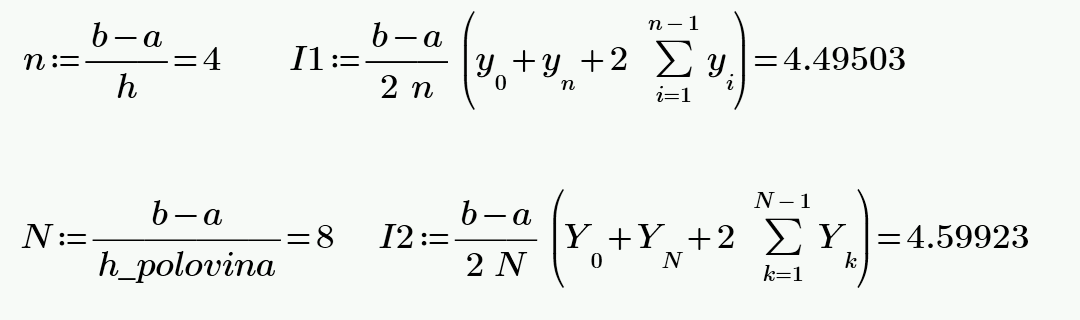
Рисунок 3.3. – Вычисление интеграла функции .

Таблица 3.2. – Значения интегралов.

	Значение вычисленного интеграла

Была произведена оценка погрешности по правилу Рунга. Она составила . В предыдущих лабораторных работах была обозначена планка в максимально допустимую погрешность в , поэтому здесь была взята она же. Число, получившееся в результате оценки погрешности по правилу Рунга получилось не больше установленной погрешности, что свидетельствует о правильности расчётов (см. рисунок 3.4)

Рисунок 3.4. – Оценка погрешности по правилу Рунга.

4. Вывод.

Было выполнено численное интегрирование функции , значения интегралов были записаны в таблицы. Из проделанной работы можно сделать вывод, что метод Симпсона гораздо более точный, тем метод трапеций. Сравнение этих методов представлено в таблице 4.1. На рисунке 4.1 представлен. Посчитанные интегралы можно сравнить с компьютерным расчётом (см. рисунок 4.1). Как можно заметить, посчитанные интегралы методом Симпсона и методом трапеций похожи на компьютерный расчёт.

Таблица 4.1. – Значения интегралов в сравнении.

Метод Симпсона (		Метод трапеций

Рисунок 4.1. – Компьютерный расчёт интеграла заданной функции.