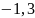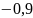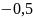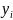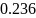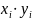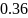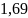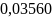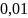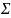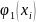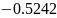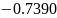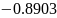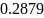ЛР-0003 (Аппроксимация функций. Метод наименьших квадратов) / chm_lab_0003_final
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И
МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский Технический Университет Связи и Информатики»
Кафедра «Информатика»
Лабораторная работа №3
«Аппроксимация функций. Метод наименьших квадратов.»
по дисциплине
«Численные Методы»
Выполнил студент гр. XXXX:
https://t.me/mattervisualizer
Проверил:
Москва, 2023 г.
Содержание.
Индивидуальное задание.
В данной лабораторной работе необходимо
выполнить аппроксимацию функции
методом наименьших квадратов по заданным
узлам
(вариант 6), выполнить линейную
аппроксимацию, с помощью математического
пакета (Mathcad) получить
аппроксимирующие полиномы МНК 1, 2, 3, 4 и
5-ых степеней, соответствующие им СКО и
построить графики полученных полиномов.
Аппроксимация методом наименьших квадратов.
Для решения задачи аппроксимации методом наименьших квадратов была выбрана функция, заданная следующей таблицей. (см. таблицу 2.1)
Таблица 2.1. —
Значения функции
от
узлов 0, 1, 2, 3, 4, 5 и 6.
Значения элементов матрицы Грама и столбцов свободных членов представлены в таблице 2.2.
Таблица 2.2. — Значения элементов матрицы Грама и столбцов свободных членов.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение системы уравнений, поиск исходной функции аппроксимации, её значения в узлах и среднеквадратичное отклонение представлены на рисунке 2.1 и ниже, а также в таблице 2.3.
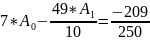
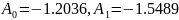
Тогда полином первой степени имеет вид
.
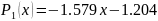Среднеквадратичное отклонение считается
по следующей формуле:
Рисунок 2.1. — Решение системы уравнений; поиск исходной функции аппроксимации, её значения в узлах и среднеквадратичное отклонение (оценка погрешности).
Таблица 2.3. — Исходная функция аппроксимации, её значения в узлах и среднеквадратичное отклонение (оценка погрешности).
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
Приближённый (линейно аппроксимированный) график функции представлен на рисунке 2.2.
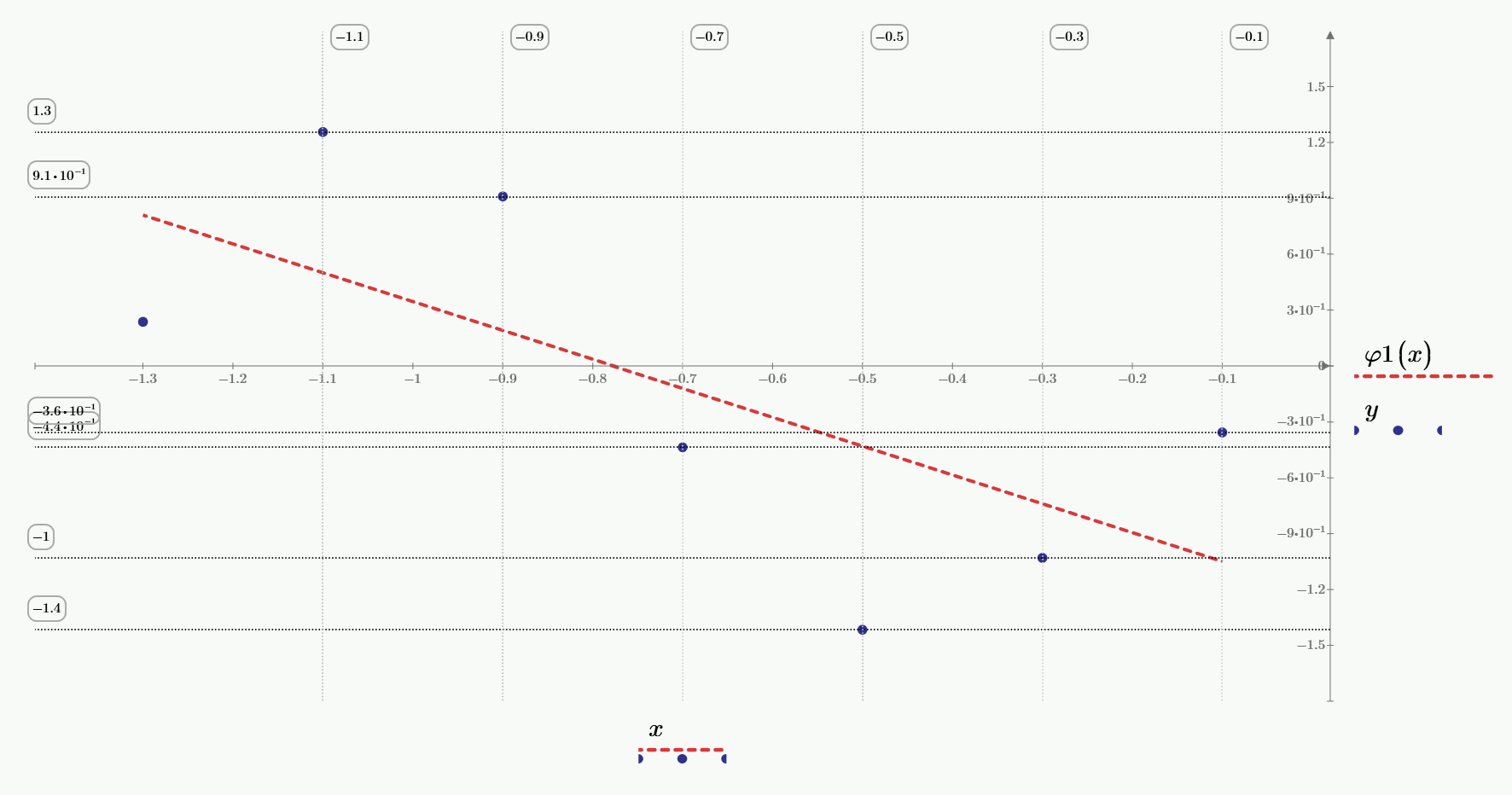
Рисунок 2.2. — График
линейная
аппроксимация функции
).
Аппроксимация с использованием математического пакета; получение полиномов МНК 1, 2, 3, 4 и 5-ых степеней и их СКО.
Посчитанные полиномы МНК 1, 2, 3, 4 и 5-ых степеней и их среднеквадратичное отклонение представлены на рисунках 3.1 – 3.5. Данные о значениях полиномов в узлах перенесены в таблицу 3.1.
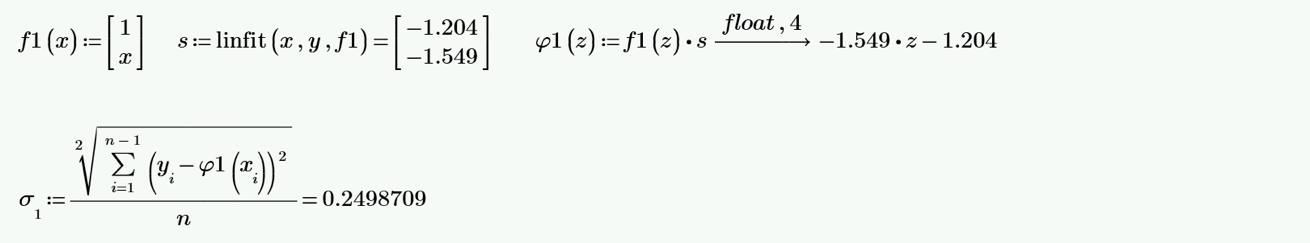
Рисунок 3.1. — Полином МНК первой степени, его СКО.
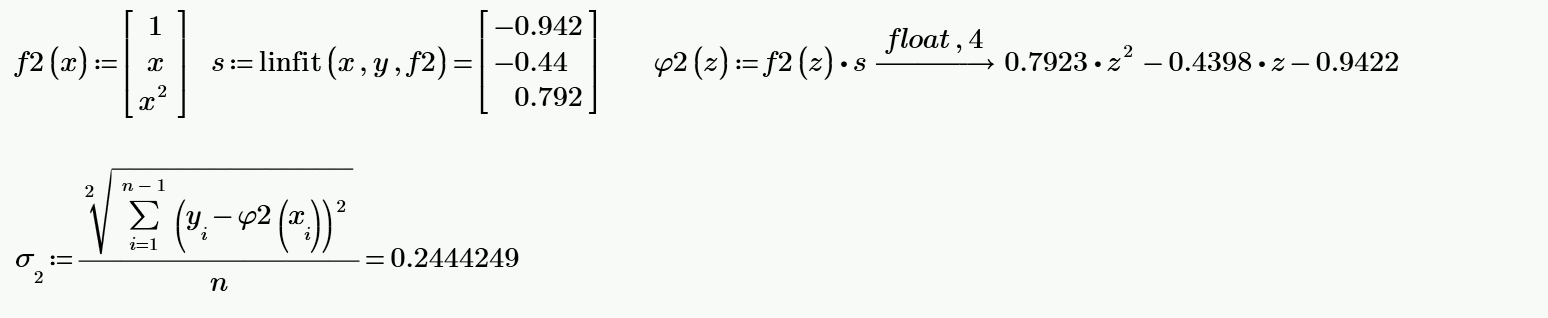
Рисунок 3.2. — Полином МНК второй степени, его СКО.
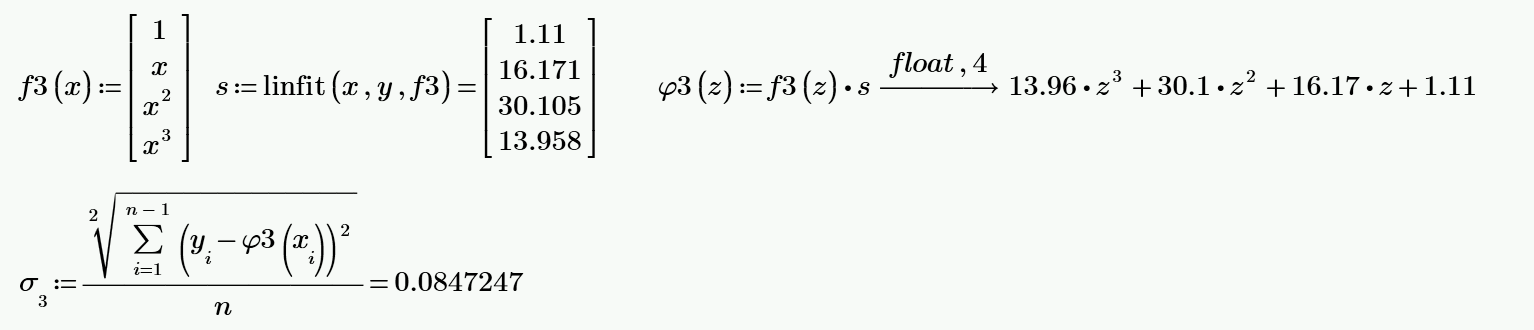
Рисунок 3.3. — Полином МНК третьей степени, его СКО.
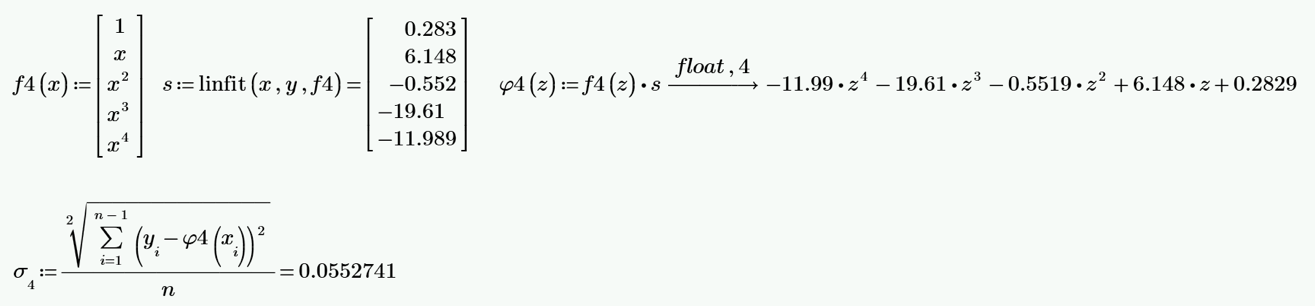
Рисунок 3.4. — Полином МНК четвётой степени, его СКО.
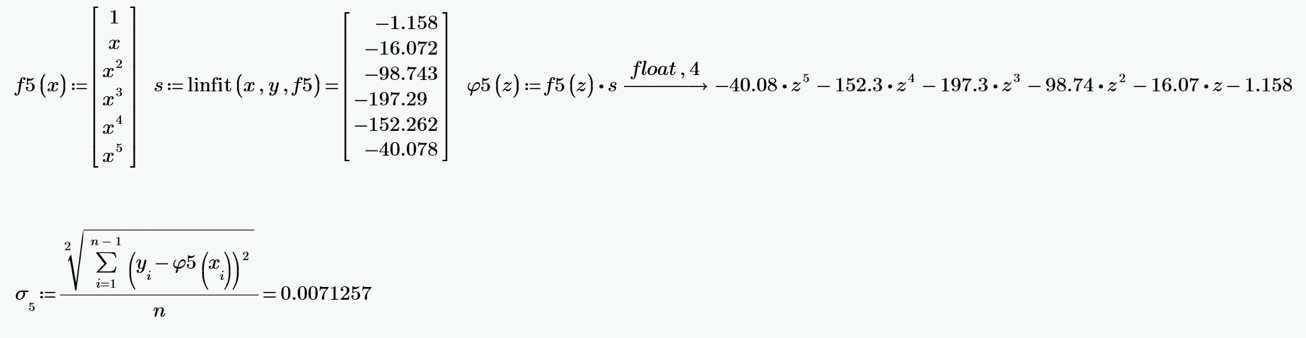
Рисунок 3.5. — Полином МНК пятой степени, его СКО.
Таблица 3.1. — Значения каждого из 5 полиномов МНК, их СКО.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приближённые (квадратично аппроксимированные) графики функции представлены на рисунке 3.2.
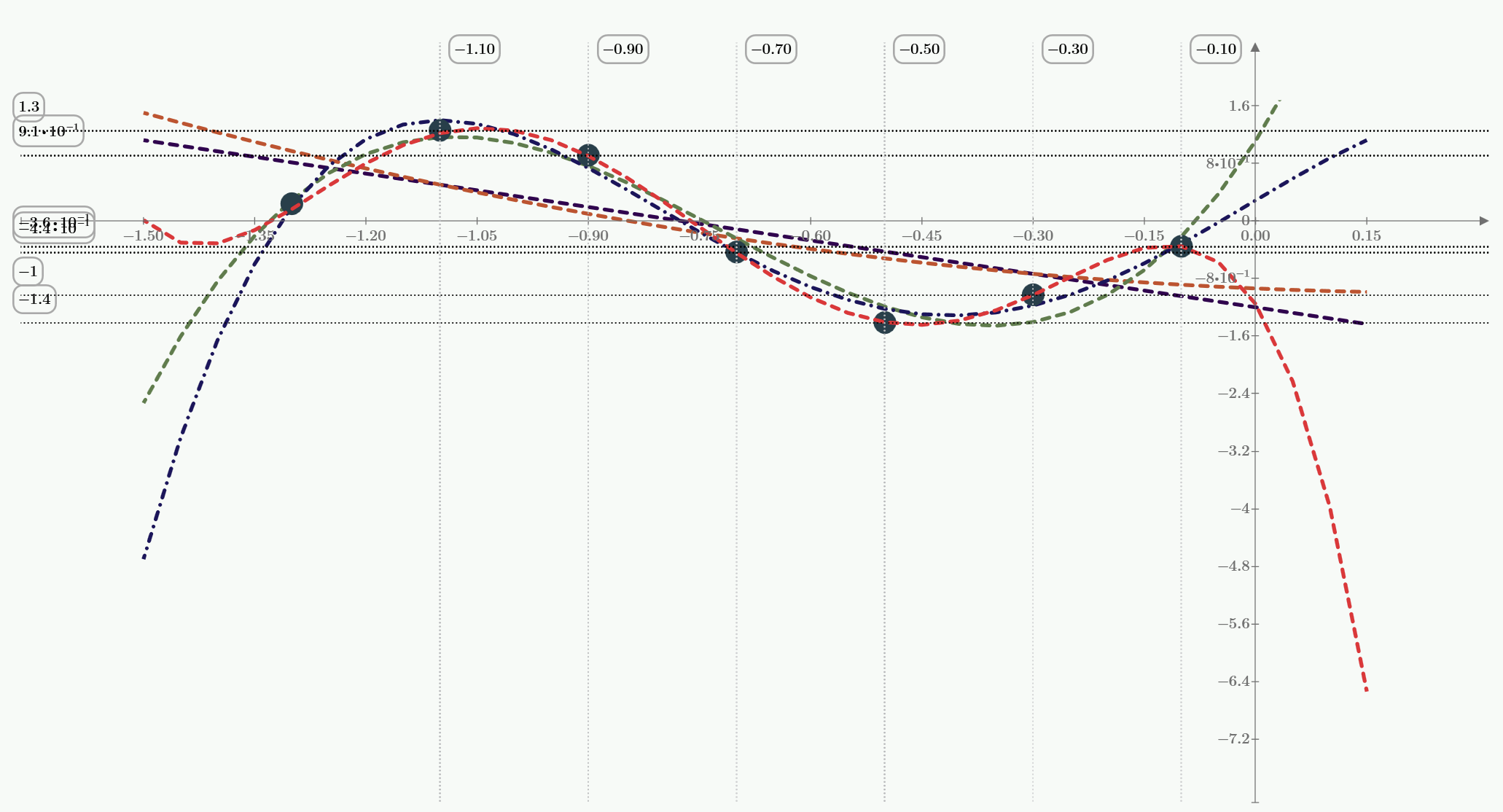
Рисунок 3.2. — Графики полиномов МНК квадратичная аппроксимация функции разных степеней).
Вывод.
Была выполнена линейная и квадратичная
аппроксимация функции
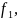значения аппроксимированных функций
были записаны в таблицы и построены их
графики. Из проделанной работы можно
сделать вывод, что квадратичная
аппроксимация 5-ой степени уже достаточно
приближена к аппроксимируемой функции.