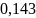ЛР-0002 (Интерполяция функций) / chm_lab_0002_final
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И
МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра «Информатика»
Лабораторная работа №2
«Интерполяция функций»
по дисциплине
«Численные методы»
Выполнил студент гр:
https://t.me/mattervisualizer
Проверил:
Москва, 2023 г.
Содержание.
1. Общее задание. 3
2. Метод Лагранжа. 4
3. Метод Ньютона. 7
4. Вывод. 11
Общее задание.
В данной лабораторной работе необходимо
выполнить вручную интерполяцию методами
Лагранжа в точке
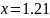 и метод Ньютона в точке
и метод Ньютона в точке
 .
Необходимо записать интерполяционные
формулы 1-ой, 2-ой и 3-ей степени полинома,
выполнить расчёты по каждой интерполяционной
формуле и вычислить погрешность для
обоих методов.
.
Необходимо записать интерполяционные
формулы 1-ой, 2-ой и 3-ей степени полинома,
выполнить расчёты по каждой интерполяционной
формуле и вычислить погрешность для
обоих методов.
Метод Лагранжа.
Вся работа была выполнена в математическом пакете Mathcad. Первым делом вычисления будут производиться методом Лагранжа (рисунок 2.1.)

Рисунок 2.1. – Перенесённые данные.
Здесь
 – номер узла,
– номер узла,
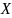 – данный корень. Таблица
– данный корень. Таблица
 – значения, которые приближены к
исходному корню, а5 таблица
– значения, которые приближены к
исходному корню, а5 таблица
 – значение функции, взятое из таблицы,
представленной в методических материалах.
Запишем значения в таблицу (см. таблицу
2.1).
– значение функции, взятое из таблицы,
представленной в методических материалах.
Запишем значения в таблицу (см. таблицу
2.1).
Таблица 2.1. – Приближённые значения
и соответствующие им значения

Номер узла |
x |
y |
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
После переноса данных в Mathcad были вычислениы полиномов Лагранжа. (рисунок 2.2.)

Рисунок 2.2. – Вычисления полиномов Лагранжа 1, 2 и 3 степени.
Проверка вычисления полиномов Лагранжа ручным расчётом выполнена и показана ниже. (рисунок 2.3.)

Рисунок 2.3. – Ручной расчёт вычисления полиномов Лагранжа 1, 2 и 3 степени и сравнение с машинным расчётом.
Машинный и ручной расчёт идентичны, что означает правильность вычислений. Для удобства все значения вычисленных полиномов Лагранжа записаны в таблицу (см. таблицу 2.2).
Таблица 2.2. – Значения полиномов Лагранжа 1, 2 и 3 степени.
|
|
|
|
|
|
Полиномы Лагранжа вычислены. Ниже представлены вычисления оценок погрешностей полиномов Лагранжа 1-ой и 2-ой степени (рисунок 2.3)
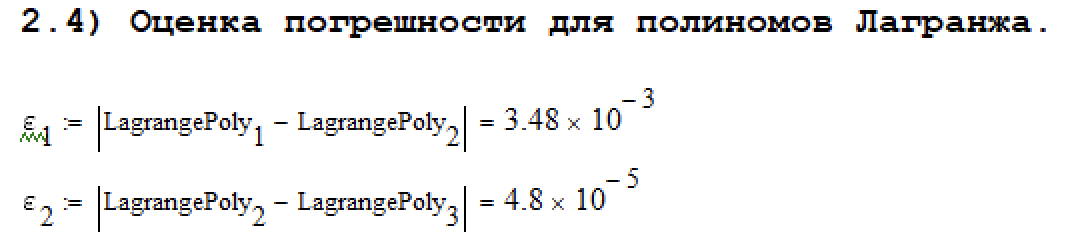
Рисунок 2.4. – Оценка погрешностей для полиномов Лагранжа 1-ой и 2-ой степени.
Перенесём полученные данные в таблицу (см. таблицу 2.3).
Таблица 2.3. – Оценка погрешностей для полиномов Лагранжа.
|
|
Погрешность |
|
|
|
|
|
|
|
|
|
Погрешность
 (последней из произведённых, в которой
можно оценить эту самую погрешность)
получилась меньше, чем 0.001, из чего
следует правильность расчёта.
(последней из произведённых, в которой
можно оценить эту самую погрешность)
получилась меньше, чем 0.001, из чего
следует правильность расчёта.
Метод Ньютона.
Переходим к методу Ньютона. Перенесённые данные представлены ниже (рисунок 3.1)

Рисунок 3.1. – Перенесённые данные.
Здесь
– номер итерации,
 – данный корень. Таблица
– данный корень. Таблица
 –
значения, которые приближены к исходному
корню, а таблица
–
значения, которые приближены к исходному
корню, а таблица
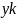 – значение функции, взятое из таблицы,
представленной в методических материалах.
Значения были записаны в таблицу ниже.
(см. таблицу 3.1.)
– значение функции, взятое из таблицы,
представленной в методических материалах.
Значения были записаны в таблицу ниже.
(см. таблицу 3.1.)
Таблица 3.1. – Приближённые значения и соответствующие им значения
x |
y |
|
|
|
|
|
|
|
|
Вычисление конечных разностей 1-ого, 2-ого и 3-его порядка представлены ниже (рисунок 3.2.)

Рисунок 3.2. – Вычисление конечных разниц 1-ого, 2-ого и 3-его порядков.
Для удобства все значения вычисленных конечных разниц записаны в таблицу (см. таблицу 3.2).
Таблица 3.2. – Приближённые значения и соответствующие им значения и конечные разницы 1-ого, 2-ого и 3-его порядков.
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисленные полиномы Ньютона показаны
ниже. (рисунок 3.3), где
 - шаг для узлов.
- шаг для узлов.

Рисунок 3.3. – Вычисление полиномов Ньютона.
Машинный и ручной расчёт идентичны, что означает правильность вычислений. Для удобства все значения вычисленных полиномов Лагранжа записаны в таблицу (см. таблицу 3.3).
Таблица 3.3. – Значения полиномов Ньютона 1, 2 и 3 степени.
|
|
|
|
|
|
Полиномы Ньютона вычислены. Ниже представлены вычисления оценок погрешностей полиномов Ньютона 1-ой и 2-ой степени (рисунок 3.4)
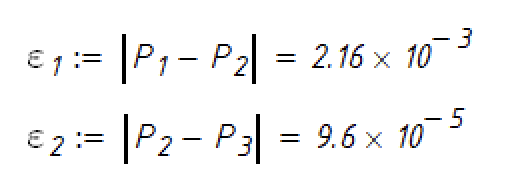
Рисунок 3.4. – Оценка погрешностей для полиномов Ньютона 1-ой и 2-ой степени.
Полученные данные перенесены в таблицу ниже. (см. таблицу 3.4)
Таблица 3.4. – Оценка погрешностей для полиномов Ньютона.
|
|
Погрешность |
|
|
|
|
|
|
|
|
|
Погрешность (последней из произведённых, в которой можно оценить эту самую погрешность) получилась меньше, чем 0.001, из чего следует правильность расчёта.
4. Вывод.
В процессе выполнения лабораторной работы была произведена интерполяция методами Лагранжа и Ньютона и оценена погрешность этих методов. При увеличении степени полиномов обоих методов увеличивается точность вычисления (см. таблицу 4.1, таблицу 4.2 и таблицу 4.3).
Таблица 4.1. – Сравнение погрешностей путём вычислений методами Лагранжа и Ньютона.
Полином |
Точность метода Лагранжа |
Точность метода Ньютона |
|
|
|
|
|
|
Таблица 4.2. – Таблица полиномов.
Степень |
Полином Лагранжа |
Полином Ньютона |
|
|
|
|
|
|
3 |
|
|
Таблица 4.3. – Таблица значений полиномов в узлах интерполяции
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|






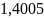






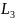



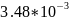
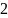










 123
123