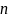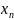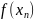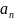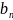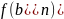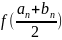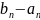МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И

МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра «Информатика»

Лабораторная работа №1

«Методы решения нелинейных уравнений»

по дисциплине

«Численные методы»

Выполнил студент гр. БББ0000:

https://t.me/mattervisualizer

Проверил:

Москва, 2023 г.

Содержание.

1. Общее задание. 3

2. Ход работы. 4

3. Этап отделения корней. 5

4. Этап уточнения корней (метод хорд). 7

4.1. Этап уточнения корней (метод половинного деления). 10

5. Вывод. 15

1. Общее задание.

В данной лабораторной работе необходимо исследовать функцию нелинейного уравнения, данную по вариантам. В этом случае будет исследоваться уравнение 6-го варианта:

В этом уравнении необходимо найти корни уравнение двумя методами:

1. методом хорд;

2. методом половинного деления.

Также необходимо проверить погрешность и написать программу для анализа уравнения.

2. Ход работы.

Вся работа будет производится в математическом пакете Mathcad 15. Первым делом переносим данную функцию и строим её график (рис. 1)

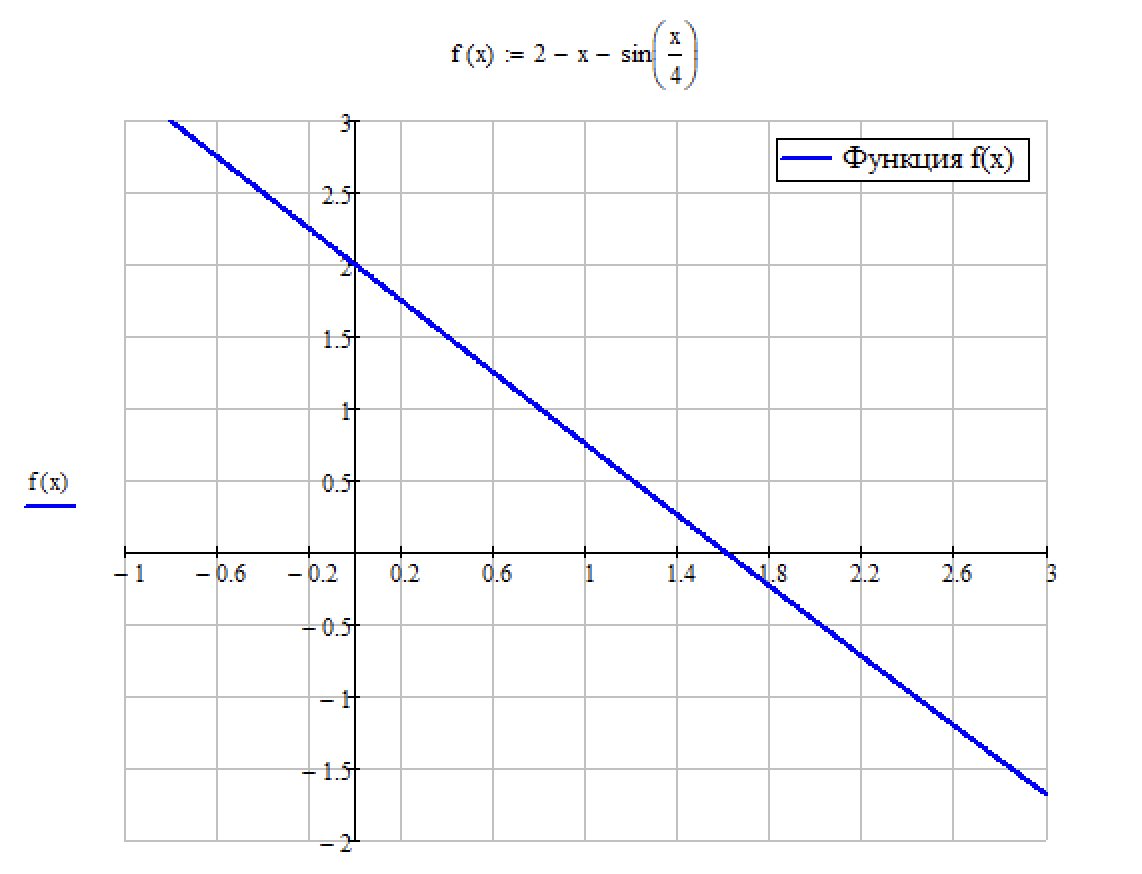
Рисунок 1. – График функции 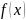(графический метод отделения корня .

3. Этап отделения корней.

Переходим к этапу отделения корней. Для этого необходим как графический метод, так и аналитический. График уже построен выше (рис. 1), а аналитический метод представлен ниже (рис. 2).

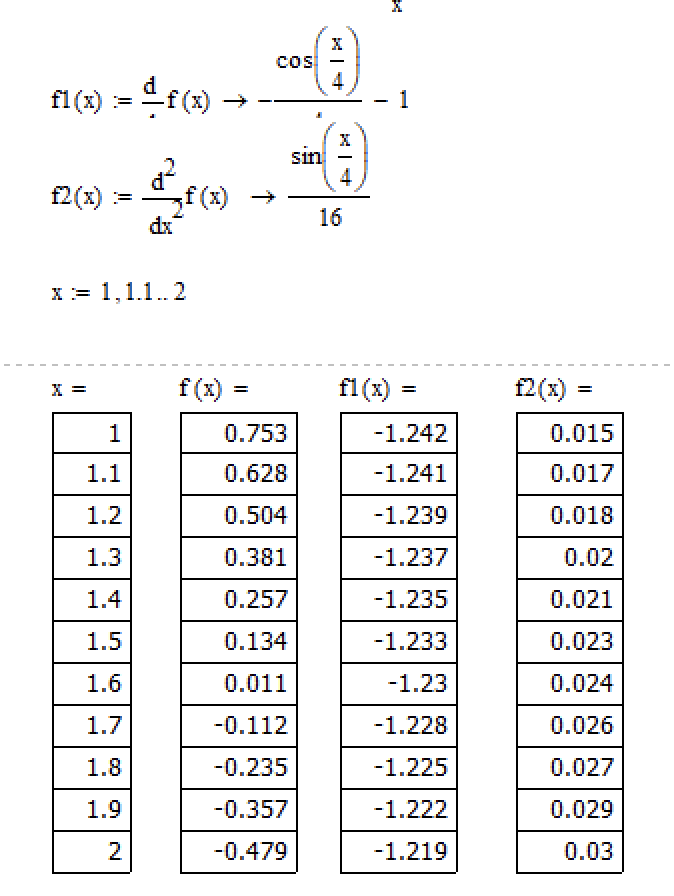
Рисунок 2. – Аналитический метод отделения корня , таблица первых и вторых производных функции , её значения и значения .

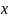На графике функции видно, что корень один (там, где он пересекает ось абсцисс). Это промежуток .

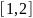Для аналитического метода понадобится таблица первых и вторых производных функции , её значения и значения (рис. 2) Выбранный шаг – 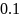, поэтому .

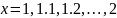Можно заметить, что значение меняет свой знак на значении из чего можно сделать вывод, что в промежутке 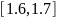существует единственный корень данного уравнения.

Значения первой производной 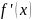, не меняется на протяжении всего промежутка , т. к. функция всегда убывает. Можно сделать вывод, что убывает всегда, хоть это и не совсем корректно.

Значения первой производной и второй производной 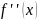будут использоваться в дальнейшем в методе хорд.

4. Этап уточнения корней (метод хорд).

Необходимые и достаточные условия сходимости для метода хорд:

1. непрерывна на 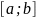и ;

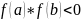2. и отличны от нуля и сохраняют знаки для

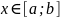
Проверим условия сходимости на промежутке (рис. 3).

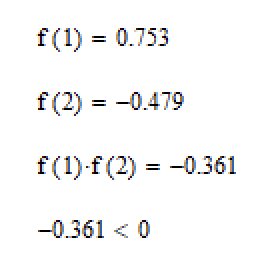
Рисунок 3. – Проверка условия сходимости.

Видно, что условие выполняется. Второе требование может быть проверено по полученной нами ранее таблице (рис. 2) где видно, что и отличны от нуля и сохраняют знаки для .

Условия сходимости выполняются.

Для вычисления методом хорд воспользуемся следующей рекуррентной формулой:

;

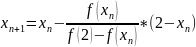Вторая производная 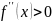, из этого следует, что функция вогнутая и, следовательно,

Расчёт в Mathcad 15 показан ниже (рис. 4).

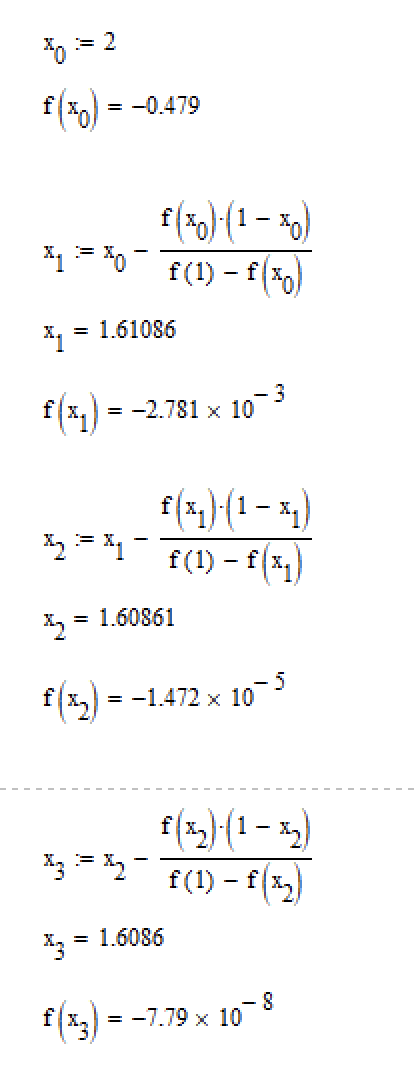
Рисунок 4. – Расчёт метода трёх хорд в Mathcad.

Построим таблицу по полученным данным (табл. 1).

Таблица 1. – Результаты расчёта методом трёх хорд в Mathcad.

0	0	-0.479
1	1.61086	-0.002781
2	1.60861	-0.000016861
3	1.6086	-0.0000000779

Оценим погрешность этих вычислений по этой формуле:

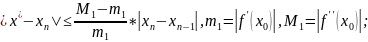
Расчёт в Mathcad 15 показан ниже (рис. 5).

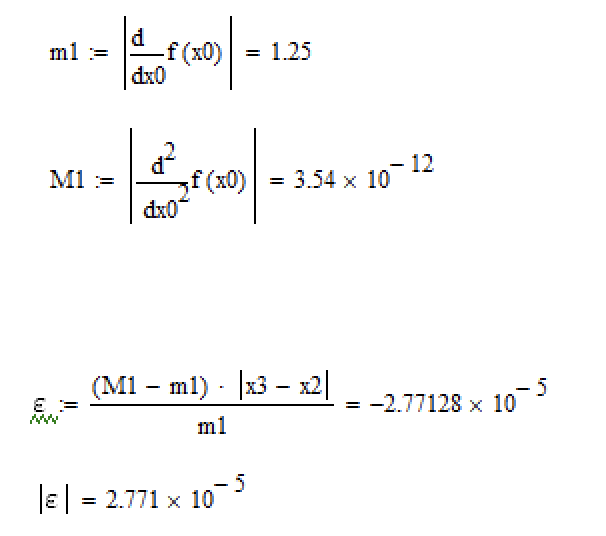
Рисунок 5. – Расчёт погрешности в Mathcad.

Полученная погрешность 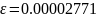, что достаточно мало.

1. Этап уточнения корней (метод половинного деления).

Необходимое и достаточное условие сходимости для метода половинного деления одно: если на отрезке существует только один корень. Это действительно так, так что условие сходимости уже доказано.

Выбираем начальное приближение. Это делается по следующей формуле:

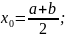
Приближаем так три раза. Все расчёты из Mathcad 15 представлены ниже (рис. 6.1 и рис. 6.2)

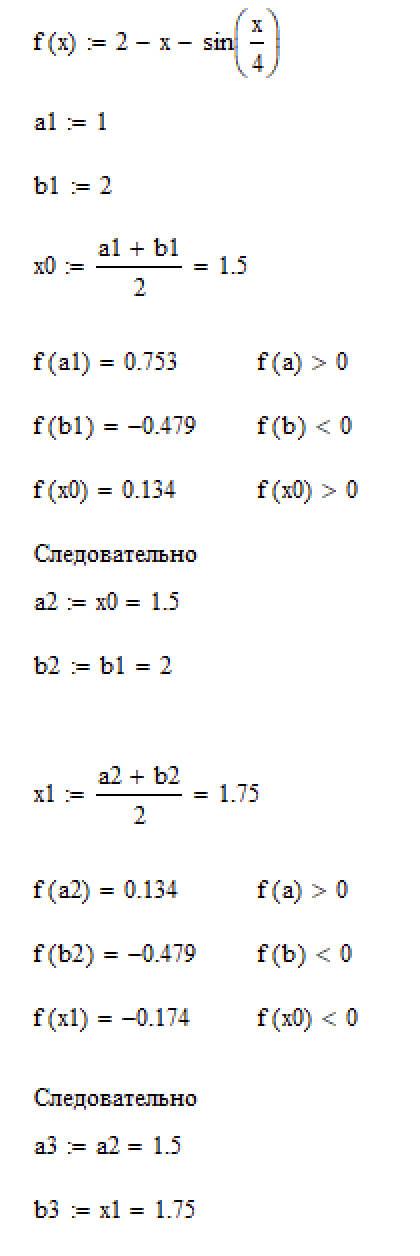
Рисунок 6.1. – Расчёт первых двух итераций метода половинного деления в Mathcad.

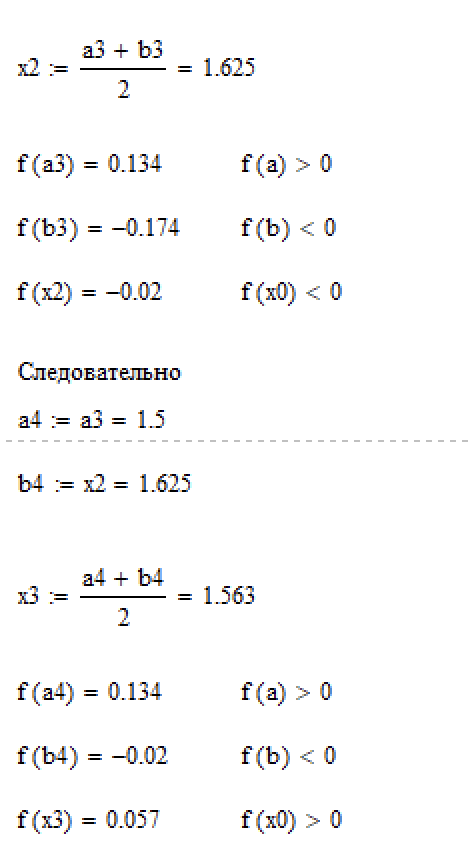
Рисунок 6.2. – Расчёт последней итерации метода половинного деления в Mathcad.

Из последней итерации видно, что корень уравнения 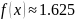. Число схоже с первым методом хорд, но гораздо менее точное. Внесём все результаты в таблицу (см. таблицу 2).

Таблица 2. – Результаты расчёта методом половинного деления в Mathcad.

0	1	2	0.753	-0.479	1.5	0.134	-1
1	1.5	2	0.134	-0.479	1.75	-0.174	-0.5
2	1.5	1.75	0.134	-0.174	1.625	-0.174	-0.25
3	1.5	1.625	0.134	-0.02	1.5625	-0.02	-0.125

Реализуем данный метод с помощью языка программирования C++. Программный код представлен ниже (см. листинг 1).

#include <cmath>

#include <iostream>

double fx(double x)

{

double function = 2 - x - sin(x/4);

return function;

};

int main()

{

double a, b, c, e;

std::cout << "[a] Введите нижнюю границу промежутка > ";

std::cin >> a;

std::cout << "[b] Введите верхнюю границу промежутка > ";

std::cin >> b;

std::cout << "[e] Задайте точность (чем меньше число, тем точнее) > ";

std::cin >> e;

int i = 0;

while (b - a > e)

{

i++;

c = (a + b)/2;

if (fx(b) * fx(c) < 0)

{

a = c;

}

else

{

b = c;

}

std::cout << "Итерация: " << i << "; " << (a + b)/2 << "\n";

}

return 0;

}

Листинг 1. – Программный код для реализации метода половинного деления на языке C++.

Данная программа получает на вход три значения: 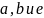. 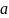и 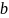– переменные, обозначающие верхний и нижний пределы промежутка, а 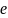– точность, с которой вычисляется корень уравнения.

В ручном расчёте точность можно вычислить по формуле:

;

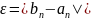Исходя из выше полученных данных (табл. 1) точность расчёта третий итерации равна .

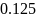Проверим программу на работоспособность, написав туда необходимые значения (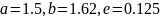 ). Вывод программы показан ниже (рис. 7).

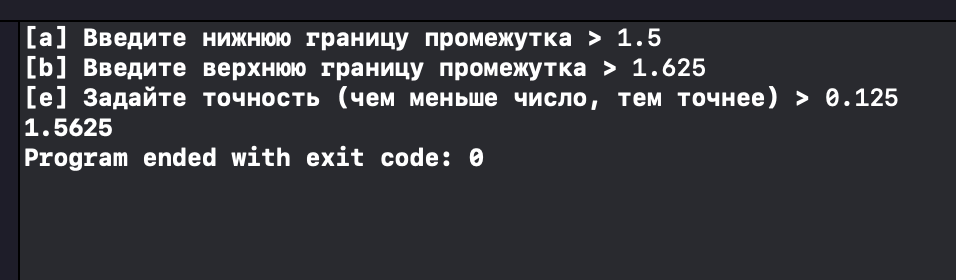
Рисунок 7. – Вывод программы.

Значение совпадает с тем, которое было получено ручным счётом, что говорит о правильности написания программы.

Рассчитаем корень с другими точностями (таблица 2).

Точность	Корень
0.1	1.59475
0.01	1.60547
0.001	1.60811
0.0001	1.6086

Таблица 2. – Результаты расчёта методом половинного деления с заданными точностями.

5. Вывод.

В процессе выполнения лабораторной работы был уточнён участок нахождения корня уравнения аналитическим и графическим методами. При отделении корня было решено анализировать промежуток .

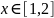Также было произведено сравнение метода половинного деления с методом хорд и половинного деления. Результаты сравнения приложены в таблице 3.

Таблица 3. – Сравнение метода хорд и половинного деления.

Номер итерации	Метод хорд	Половинное деление
0	0	2
1	1.61086	2
2	1.60861	1.75
3	1.6086	1.625