9. Дискретизация выбранного непрерывного регулятора

По полученной ранее непрерывной передаточной функции регулятора получим дискретную передаточную функцию регулятора. Для этого необходимо определить период квантования . Найти верхнюю границу для этого параметра можно из неравенства:

где – частота среза ЛАЧХ разомкнутой модели, – допустимое значение погрешности аппроксимации (примем или ).

Рисунок 9. ЛАЧХ разомкнутой линейной системы с выбранным регулятором.

Определение дискретной передаточной функции по известной передаточной функции регулятора возможно с помощью кода MATLAB:

Wreg = tf([20 20],[1 0])

dregulator=c2d(Wreg,1/75.3*pi))

Таким образом, дискретная передаточная функция имеет вид:

dregulator =

20 z - 19.92

------------

z – 1

Чтобы была возможность выставлять начальные условия, представим полученный регулятор в форме пространств состояний, используя следующие команды:

>> [Ad,Bd,Cd,Dd]=ssdata(dregulator);

>> ddregulator=ss(Ad,Bd,Cd,Dd, (1/75.3*pi))

Полученные матрицы A, B, C, D дискретизированного непрерывного регулятора:

A =

x1

x1 1

B =

u1

x1 0.25

C =

x1

y1 0.3382

D =

u1

y1 20

Импортируем из рабочего пространства MATLAB, полученный регулятор в Simulink модель, с помощью блока LTI System для дальнейшего сравнения.

10. Сравнение характеристик системы при дискретном регуляторе и непрерывном регуляторе, синтезированном «в большом».

Произведем сравнительный анализ поведения системы аналогично п. 10 при использовании различных регуляторов.

10.1 При переходе с номинального режима на заданный.

Рассмотрим поведение системы при переходе с номинального на заданный режим. На рисунках 11.1.1. – 11.1.4. представлены соответствующие графики.

Для сравнения показателей качества сведем их в таблицу, представленную ниже (таблица 5).

Рисунок 10.1.1. Переход системы с номинального режима на заданный при непрерывном и дискретном регуляторах. Сигнал , выход системы.

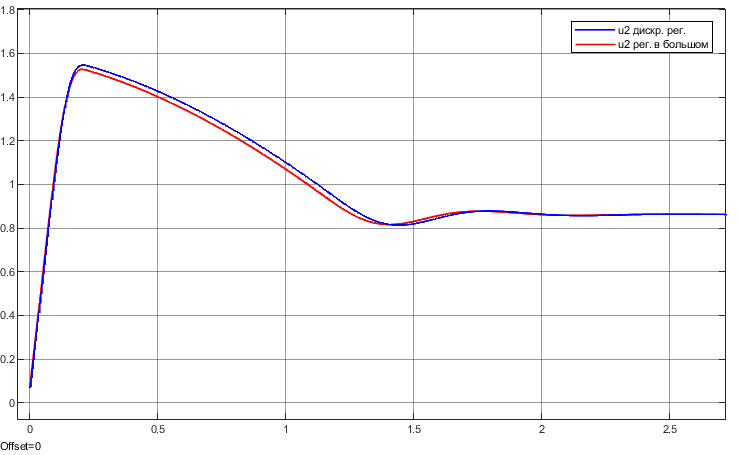
Рисунок 10.1.2. Переход системы с номинального режима на заданный при непрерывном и дискретном регуляторах. Сигнал , выход регулятора.

Рисунок 10.1.3. Переход системы с номинального режима на заданный при непрерывном и дискретном регуляторах. Сигнал , выход преобразователя.

Рисунок 10.1.4. Переход системы с номинального режима на заданный при непрерывном и дискретном регуляторах. Сигнал , выход исполнительного механизма.

Таблица 5

Регулятор	«в большом»	Дискретный
	6.5	6.6
	1.141	1.153

Как можно видеть по таблице 5, регуляторы обеспечивают почти одинаковое качество процессов, но дискретный регулятор немного «отстает» от непрерывного в выдаче управляющего воздействия, что неизбежно при дискретизации.