3. Анализ поведения системы при переходе с номинального режима на заданный

Для анализа перехода системы с номинального режима на заданный примем вектор начальных условий равным вектору равновесного состояния для номинального режима . Для интегрирования будем использовать метод Рунге-Кутта 4 и 5-го порядка (ode45) с малым шагом . На рисунках 4-7 представлены графики переходных процессов в системе.

Рисунок 3.1. Переход системы с номинального режима на заданный. Сигнал на выходе ПИ-регулятора

Рисунок 3.2. Переход системы с номинального режима на заданный. Сигнал на выходе преобразователя

Рисунок 3.3. Переход системы с номинального режима на заданный. Сигнал на выходе ИМ

Рисунок 3.4. Переход системы с номинального режима на заданный. Сигнал на выходе системы

Как можно видеть из рисунков при единичных параметрах система устойчива. В дальнейшем произведем синтез регулятора для улучшения качества процессов. Приблизительное время интегрирования данным методом составило 15 секунд, время засекалось секундомером.

4. Определение максимального допустимого шага для методов численного интегрирования

Найдем для методов одношагового (Эйлера, Гойна) и многошагового численного интегрирования (Адамса, Гира, Рунге-Кутта 2 и 3-го порядков) максимальный фиксированный шаг интегрирования , при котором ещё сохраняется устойчивость численного метода и качество процессов. Для определения времени, затрачиваемого на интегрирование, используем следующие команды MATLAB:

t=cputime; % записываем время перед запуском симуляции

sim('pressure'); % запуск симуляции

time=cputime-t; % затраченное время = текущее время – время начала симуляции.

Метод Эйлера ode1:

Максимальный шаг интегрирования, при котором сохраняется качество процессов . Время моделирования составило 5.6 сек.

Полученные графики процессов перехода с номинального режима на заданный:

Рисунок 4.1. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode2, шаг h=0.0276.

Рисунок 4.2. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode2, шаг h=0.02802.

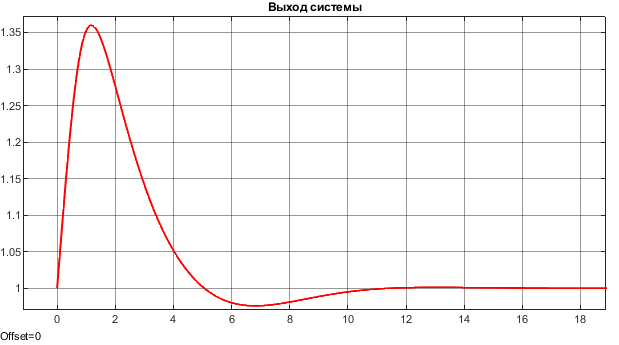
Рисунок 4.3. Переход системы с номинального режима на заданный. Сигнал на выходе системы , метод интегрирования ode1, шаг h=0.0276.

Метод Гойна (Heun) ode2:

Максимальный шаг интегрирования, при котором сохраняется качество процессов . Время моделирования составило 6.625сек.

Полученные графики процессов перехода с номинального режима на заданный:

Рисунок 4.4. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode2, шаг h=0.0435.

Рисунок 4.5. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode2, шаг h=0.0436.

Рисунок 4.6. Переход системы с номинального режима на заданный. Сигнал на выходе системы , метод интегрирования ode1, шаг h=0.0435.

Метод Bogacki-Shampine ode3:

Максимальный шаг интегрирования, при котором сохраняется качество процессов . Время моделирования составило 7.53 сек.

Полученные графики процессов перехода с номинального режима на заданный:

Рисунок 4.7. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode3, шаг h=0.047.

Рисунок 4.8. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode23, шаг h=0.0475.

Рисунок 4.9. Переход системы с номинального режима на заданный. Сигналы метод интегрирования ode3, шаг h=0.047.

Метод Bogacki-Shampine ode4:

Максимальный шаг интегрирования, при котором сохраняется качество процессов . Время моделирования составило 9.9 сек.

Полученные графики процессов перехода с номинального режима на заданный:

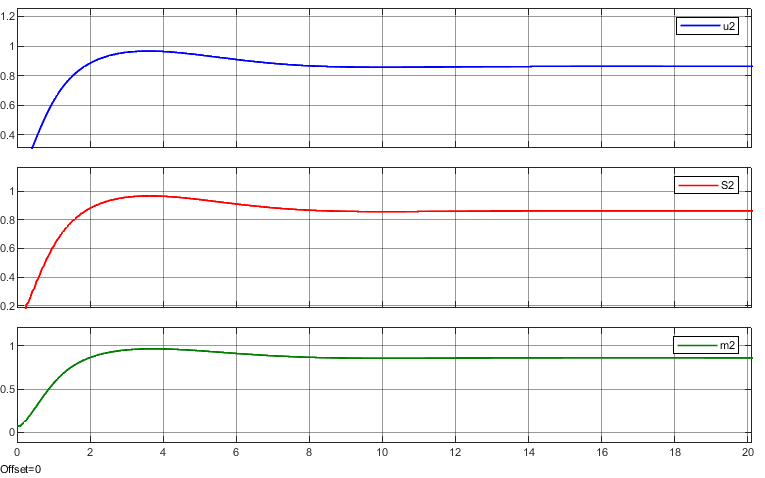
Рисунок 4.10. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode4, шаг h=0.052.

Рисунок 4.11. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode4, шаг h=0.053.

Рисунок 4.12. Переход системы с номинального режима на заданный. Сигналы метод интегрирования ode3, шаг h=0.052.

Метод Рунге-Кута 2 и 3-го порядков ode23:

Максимальный шаг интегрирования, при котором сохраняется качество процессов . Время моделирования составило 7.53 сек.

Полученные графики процессов перехода с номинального режима на заданный:

Рисунок 4.13. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode23, шаг h=0.047.

Рисунок 4.14. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode23, шаг h=0.048.

Рисунок 4.15. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode23, шаг h=0.047.

Метод Адамса ode113:

Максимальный шаг интегрирования, при котором сохраняется качество процессов . Время моделирования составило 3.41 сек.

Полученные графики процессов перехода с номинального режима на заданный:

Рисунок 4.16. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode113, шаг h=0.0134.

Рисунок 4.17. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode113, шаг h= 0.0135.

Рисунок 4.18. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode113, шаг h=0.0134.

Метод Гира ode15s:

Максимальный шаг интегрирования, при котором метод сходится . Время моделирования составило 6.19 сек.

Полученные графики процессов перехода с номинального режима на заданный:

Рисунок 4.19. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode15s, шаг h=0.2395.

Рисунок 4.20. Переход системы с номинального режима на заданный. Сигналы метод интегрирования ode15s, шаг h=0.2395.

При увеличении шага до получаем ошибку, так как метод не сходится, ошибка моделирования многократно возрастает и не укладывается в установленный предел:

An error occurred while running the simulation and the simulation was terminated

Caused by:

• Solver encountered an error while simulating model 'pressure' at time 0.23999999999999999 and cannot continue. Please check the model for errors. 

  • Nonlinear iteration is not converging with step size reduced to hmin (0.24) at time 0. Try reducing the minimum step size and/or relax the relative error tolerance. 

Результаты исследования различных методов численного интегрирования приведены в таблице 2. Для всех методов относительная ошибка составила .

Таблица 2

Метод интегрирования	Максимальный шаг h	Длительность моделирования, сек
Одношаговые методы
Метод Эйлера (ode1)	0.0276	5.6
Метод Гойна (ode2)	0.0435	8.9
Метод Bogacki-Shampine (ode3)	0.047	6.625
Метод Рунге-Кутта (ode4)	0.052	9.9
Многошаговые методы
Метод Рунге-Кутта (ode23)	0.047	7.53
Метод Адамса (ode113)	0.0134	3.41
Метод Гира (ode15s)	0.2395	6.19

Из рассматриваемых методов подходящим для дальнейшего исследования системы является метод Адамса (ode113), который несмотря на относительно малый максимальный шаг интегрирования, при котором сохраняется устойчивость метода и качество процессов, обеспечивает минимальное время интегрирования по сравнению с другими методами.