4. Определение максимального допустимого шага для методов численного интегрирования

Найдем для методов одношагового (Эйлера, Гойна) и многошагового численного интегрирования (Адамса, Гира, Рунге-Кутта 2 и 3-го порядков) максимальный фиксированный шаг интегрирования , при котором ещё сохраняется устойчивость численного метода и качество процессов. Для определения времени, затрачиваемого на интегрирование, используем следующие команды MATLAB:

t=cputime; % записываем время перед запуском симуляции

sim('pressure'); % запуск симуляции

time=cputime-t; % затраченное время = текущее время – время начала симуляции.

Метод Эйлера ode1:

Максимальный шаг интегрирования, при котором сохраняется качество процессов . Время моделирования составило 3.2031сек.

Полученные графики процессов перехода с номинального режима на заданный:

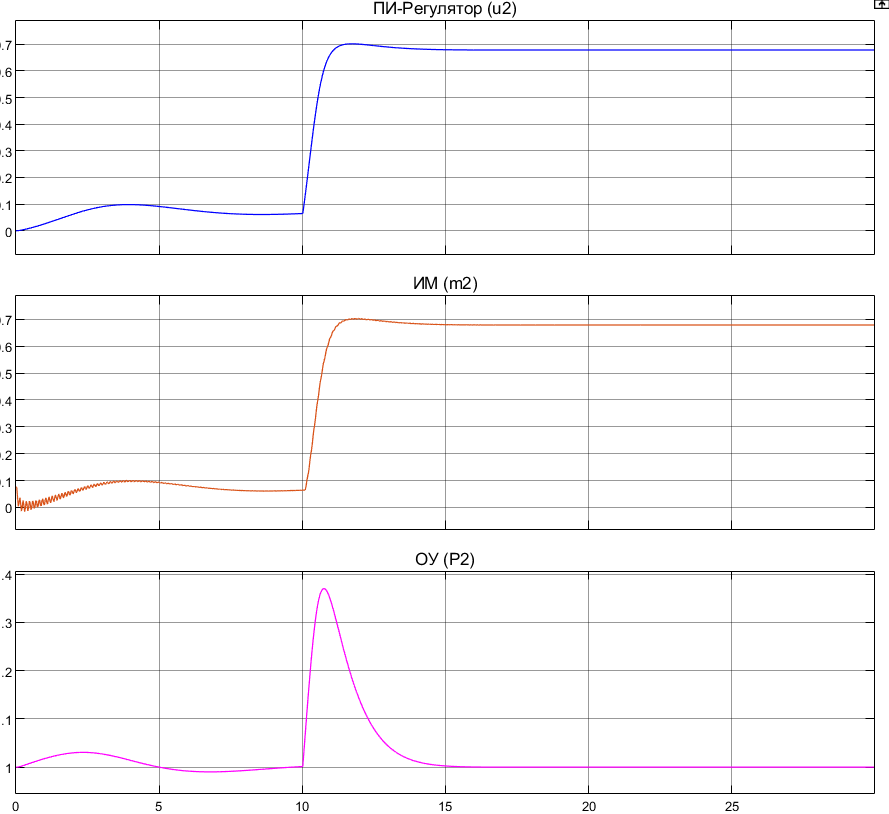
Рисунок 4.1. Переход системы с номинального режима на заданный. Сигналы метод интегрирования ode1, шаг h=0.0276.

Метод Гойна (Heun) ode2:

Максимальный шаг интегрирования, при котором сохраняется качество процессов . Время моделирования составило 3.2656.

Полученные графики процессов перехода с номинального режима на заданный:

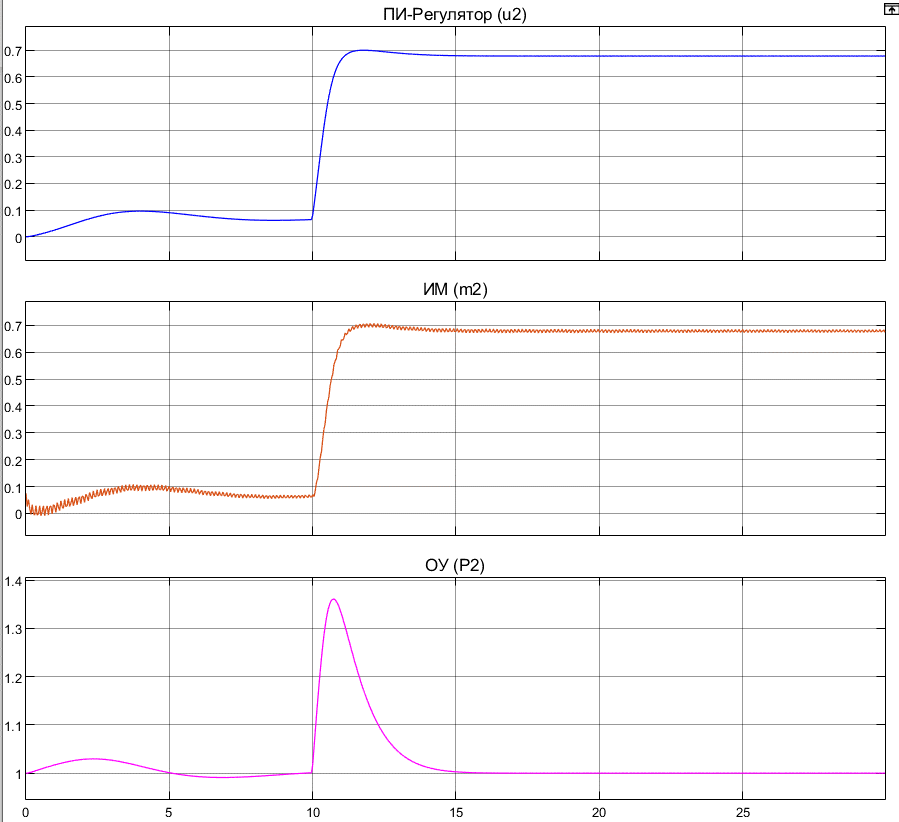
Рисунок 4.2. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode2, шаг h=0.0431.

Метод Рунге-Кутта ode4:

Максимальный шаг интегрирования, при котором сохраняется качество процессов . Время моделирования составило 9.9 сек.

Полученные графики процессов перехода с номинального режима на заданный:

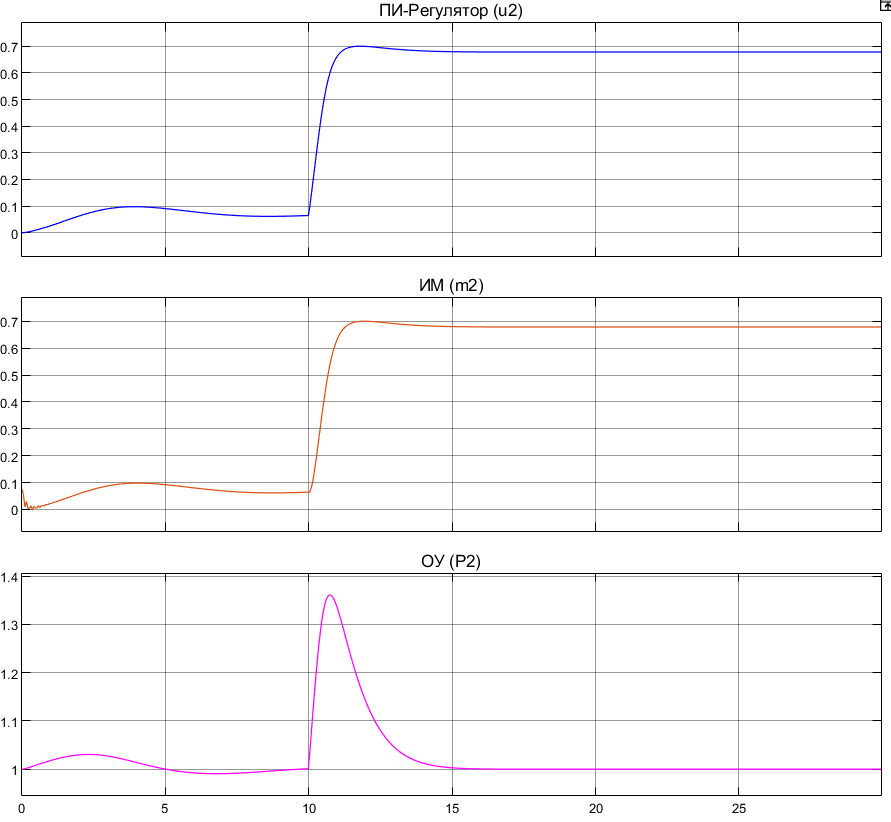
Рисунок 4.3. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode4, шаг h=0.052.

Метод Рунге-Кута 2 и 3-го порядков ode23:

Максимальный шаг интегрирования, при котором сохраняется качество процессов . Время моделирования составило 7.53 сек.

Полученные графики процессов перехода с номинального режима на заданный:

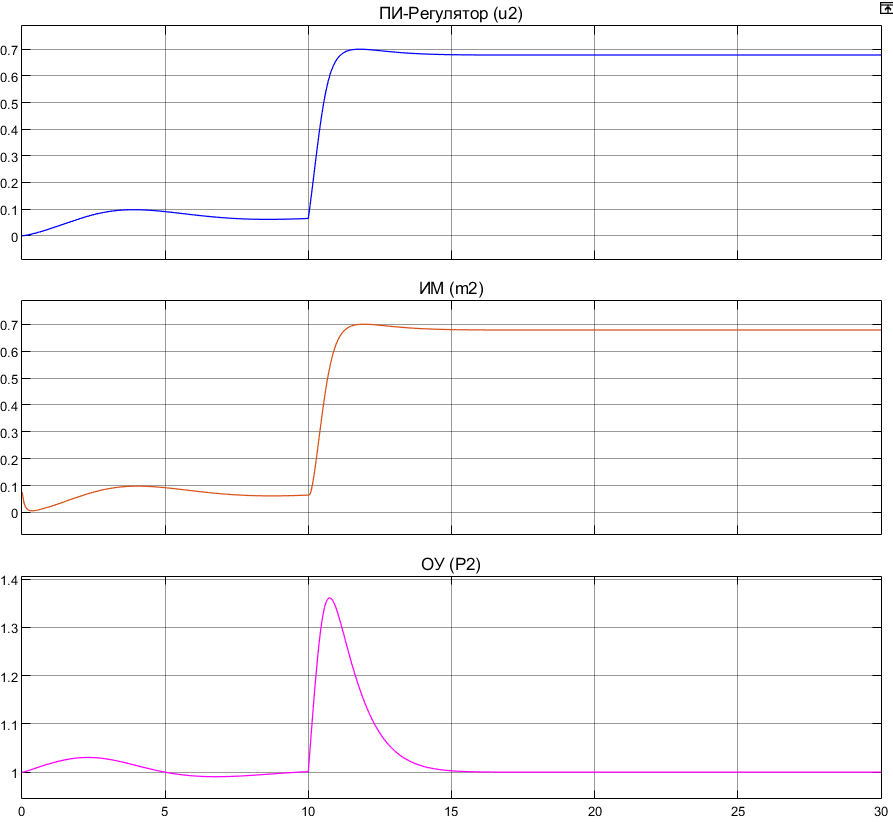
Рисунок 4.4. Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode23, шаг h=0.047.

Метод Адамса ode113:

Максимальный шаг интегрирования, при котором сохраняется качество процессов . Время моделирования составило 3.41 сек.

Полученные графики процессов перехода с номинального режима на заданный:

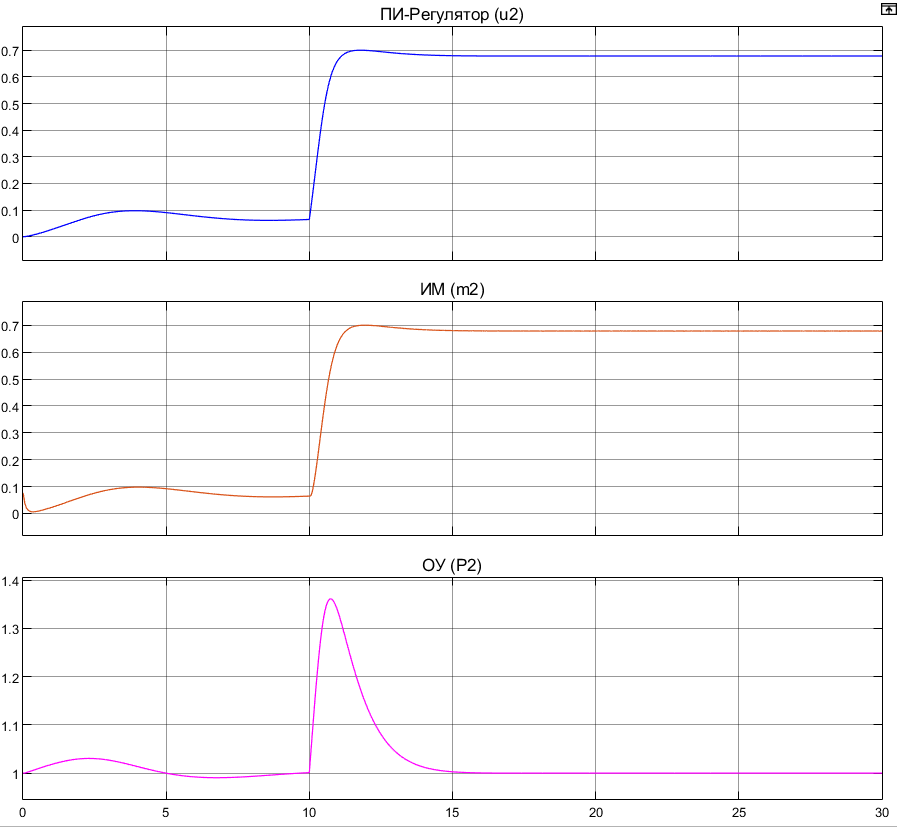
Рисунок 4.5 Переход системы с номинального режима на заданный. Сигналы , метод интегрирования ode113, шаг h=0.0134.

Результаты исследования различных методов численного интегрирования приведены в таблице 2. Для всех методов относительная ошибка составила .

Таблица 2

Метод интегрирования	Максимальный шаг h	Длительность моделирования, сек
Одношаговые методы
Метод Эйлера (ode1)	0.0276	3.2031
Метод Гойна (ode2)	0.0431	3.2656
Метод Рунге-Кутта (ode4)	0.052	3.0312
Многошаговые методы
Метод Рунге-Кутта (ode23)	0.047	3.3906
Метод Адамса (ode113)	0.01	3.2500

Из рассматриваемых методов подходящим для дальнейшего исследования системы является метод Рунге-Кутта (ode4), который имеет наибольший максимальный шаг интегрирования, при котором сохраняется устойчивость метода и качество процессов и обеспечивает минимальное время интегрирования по сравнению с другими методами.