Определение шага дискретизации при численном моделировании

До сих пор предполагалось, что исходная конечномерная модель СУ непрерывна, но при вводе в ЭВМ осуществляется её дискретизация — переход к разностной модели с выбранным шагом дискретизации (шагом интегрирования) . Однако исходная модель может быть и дискретной или дискретно-непрерывной, т. е. содержать импульсный элемент (ИЭ), работающий с периодом квантования . При численном моделировании дискретных систем между периодом квантования ИЭ и шагом интегрирования разностной схемы обычно устанавливается соотношение . Чтобы обобщить методику выбора периода квантования и шага интегрирования исходя из допустимой погрешности аппроксимации процессов при моделировании, вводится обозначение:

для непрерывных ( моделей;

для дискретных моделей.

Пусть дискретная СУ содержит реальный импульсный элемент РИЭ (рис. 1), модель которого включает идеальный импульсный элемент ИИЭ и формирующее устройство ФУ типа экстраполятора 0-го или 1-го порядка.

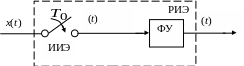
Рис. 1. Структурная схема реального импульсного элемента

На схеме принято:  — непрерывный процесс на входе РИЭ;  — модулированная последовательность -импульсов на выходе ИИЭ, причём ;  — квантованный процесс на выходе РИЭ.

Возможный вид процесса на выходе РИЭ в зависимости от типа экстраполятора изображён на рис. 2.

а б

Рис. 2. Квантование процесса

Период квантования (шаг дискретизации по времени) принимается постоянным, т. е.

Величина представляет собой максимальную абсолютную погрешность аппроксимации (экстраполяции) непрерывной функции квантованной функцией на i-м интервале времени.

Максимальная абсолютная погрешность квантования на заданном интервале моделирования процесса

,

где  — целая часть числа.

Пусть максимальное по модулю значение процесса на интервале моделирования

Тогда отношение

представляет собой приведённую к максимальному значению погрешность аппроксимации.

Требуется определить период квантования исходя из условия

,

где  — допустимое значение приведённой погрешности аппроксимации.

По существу, здесь рассматривается задача аппроксимации функции на интервале другой функцией, в частности, степенным полиномом . Например, этой аппроксимирующей функцией может быть интерполяционный полином Лежандра

(1)

где ,  — узлы интерполяции.

При аппроксимации функции с высокой точностью в широком интервале изменения аргумента степень аппроксимирующего полинома может оказаться слишком высокой, а полином (1) слишком сложным для реализации. В этом случае целесообразно интервал разбить на частей

и на каждом из отрезков аппроксимировать функцию своим полиномом . Аппроксимирующая функция , составленная из полученных таким образом кусков, называется ломаной и представляет собой кусочно-непрерывную на интервале функцию.

Возможность сколь угодно точной равномерной (с равномерным шагом) аппроксимации обеспечивается выполнением условий следующей теоремы.

Теорема. Если функция непрерывна на , то для любого существует ломаная функция (  — конечно), для которой справедливо

.

Следствие. Любая непрерывная на функция может быть аппроксимирована полиномиальной ломаной функцией . В частности, аппроксимирующая функция может быть ступенчатой ломаной или линейной ломаной . Отметим, что к классу кусочно-полино­миальных аппроксимирующих функций относятся также и так называемые полиномиальные сплайны.

Абсолютная погрешность аппроксимации функции интерполяционным полиномом Лежандра (1) определяется остаточным членом этого полинома

или

.

Возвращаясь к рассматриваемой задаче, на каждом интервале дискретизации получаем:

для

;

для

(так как , что достигается при ). Здесь  — максимальные значения модуля соответствующих производных на -м интервале дискретизации.

Для оценки максимальной погрешности аппроксимации на всем интервале моделирования процессов используется максимально возможное значение модуля соответствующей производной

,

определяемое на множестве всех интервалов дискретизации.

Следовательно, можно записать:

для  —  ; для  —  .

Возможны различные способы определения и . В частности, можно воспользоваться неравенством С. Н. Бернштейна, которое вытекает из следующего утверждения.

Утверждение. Если процесс ограничен по модулю некоторым максимальным значением , т. е. , и имеет ограниченную спектральную характеристику в диапазоне (рис. 3), то максимальное значение производной -го порядка ограничено неравенством

. (2)

Рис. 3. Ограниченная спектральная характеристика процесса

Переходные процессы, получаемые по моделям, представленным в форме систем ДУ, теоретически имеют неограниченные спектры. Однако ММ любой реальной СУ справедлива лишь в определённом диапазоне частот, поэтому в качестве можно взять границу частотного диапазона адекватности ММ.

Для линейных моделей СУ часто рекомендуется принять , где  — значение наименьшей постоянной времени.

С учетом (2) можно записать следующие соотношения:

; .

Отсюда имеем:

для  —  ;

для  —  .

Иначе можно записать:

для  —  , ;

для  —  , .

Например, при (или ):

для  —  ;

для  —  .

При использовании логарифмических амплитудно-частотных характеристик разомкнутых линейных импульсных СУ (рис. 4) учитывается ограничение .

Это неравенство согласуется с условием теоремы Шеннона–Котельникова

,

е сли .

Рис. 4. Логарифмическая амплитудно-частотная характеристика разомкнутой

линейной импульсной системы

В результате получаем

,

откуда

.

Следовательно, период квантования отвечает неравенству

.

Сравнивая это неравенство с результатами, полученными с использованием неравенства Бернштейна, находим:

для  —  ;

для  —  .

В том случае, если рассматривается исходная непрерывная модель, то для определения шага интегрирования следует принять и воспользоваться полученными соотношениями, например при выполнении курсовой работы.

60