ИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра АПУ

Отчёт

По Курсовой РАБОТе

по дисциплине «Теория автоматического управления»

Тема: Синтез систем автоматического управления перевёрнутым маятником на каретке

Студент гр. 0391		Чащин Д.
Преподаватель		Имаев Д.Х.

Санкт-Петербург

2023

содержание

Предисловие		3
1. Перевёрнутый маятник на каретке как модель управления		4
1.1.	Перевёрнутый маятник на каретке	4
1.2.	Математическая модель объекта управления	5
1.3.	Дифференциальные уравнения в форме Коши	6
2. Анализ объекта управления		7
2.1.	Компьютерное моделирование	7
2.2.	Линеаризация дифференциальных уравнений	9
2.3.	Передаточная функция объекта	10
2.4.	Анализ устойчивости положения равновесия	11
2.5.	Линеаризация модели и анализ в среде MATLAB/Simulink	11
3. Синтез системы автоматической стабилизации методом пространства состояний		12
3.1.	Синтез регулятора состояния	12
3.2.	Синтез наблюдателя состояний	17
3.3.	Динамический регулятор	18
3.4.	Оценка области притяжения положения равновесия	20
4. Синтез системы стабилизации частотным методом		22
4.1.	Частотный метод синтеза	22
5. Системы с цифровыми управляющими устройствами		30
5.1	Моделирование системы цифрового управления непрерывным объектом	30

Предисловие

Динамические модели перевернутых маятников различной конфигурации используются в научных публикациях для сравнения методов синтеза алгоритмов автоматической стабилизации, а также в учебном процессе технических университетов в качестве наглядных примеров неустойчивых объектов.

Отмечается, что многозвенные перевернутые маятники служат примерами шагающих роботов, ракет на старте, нескольких барж, которых толкает буксир и т. д. и т. п.

Целью курсового проектирования является освоение методов моделирования, анализа и синтеза систем автоматического управления с помощью современных инструментальных средств.

Для достижения цели необходимо решить следующие задачи:

- построить нелинейную математическую модель объекта управления;

- провести анализ объекта методом компьютерной имитации;

- провести анализ устойчивости, управляемости и наблюдаемости объекта по линеаризованной модели;

- синтезировать регуляторы методом пространства состояний;

- синтезировать регуляторы частотным методом;

- провести анализ нелинейных систем управления;

- выбрать алгоритмы цифрового управления непрерывным объектом.

1. Перевёрнутый маятник на каретке как модель управления

1.1. Перевернутый маятник на каретке

Принципиальная схема механического объекта — перевернутого маятника на каретке — изображена на рис. 1.1, где приняты следующие обозначения параметров:

• m – масса маятника, кг;

• M – масса каретки, кг;

• l – длина маятника, м,

а также переменных:

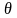• (t) – угол отклонения маятника, рад;

• x(t) – положение каретки, м;

• f(t) – сила, действующая на каретку, Н (кг*м/сек²).

Целью управления является стабилизация верхнего положения равновесия маятника.

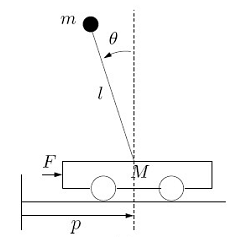
Рис. 1.1. Принципиальная схема перевернутого маятника на каретке

Рассматриваемый объект имеет две степени свободы – вращательное движение маятника и поступательное движение каретки. Управление таким объектом осложняется тем обстоятельством, что имеется только одно управляющее воздействие – сила f(t), приложенная к каретке.

1.2. Математическая модель объекта управления

Методы синтеза систем автоматического управления непрерывными объектами основаны на математических моделях в виде дифференциальных уравнений.

Рис. 1.1 можно интерпретировать как символьную модель, представленную на языке механики. Для перевода знаний с языка механики (рис. 1.1) на язык математических моделей используют законы классической механики. Такой способ построения математических моделей называют аналитическим — он возможен для объектов хорошо изученной природы.

Примем следующие допущения:

• массы маятника и каретки сосредоточены;

• отсутствуют сопротивление среды и трение.

В качестве обобщенных координат для рассматриваемой системы с двумя степенями свободы выберем y (t) — угол отклонения маятника и x(t) — положение каретки.

Математическая модель рассматриваемого объекта — система двух дифференциальных уравнений второго порядка

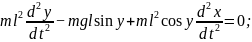(1.1)

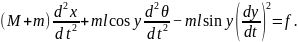(1.2)

Уравнение (1.2) представляет собой выражения баланса моментов, действующих на маятник, а уравнение (1.2) — баланса сил, действующих на каретку.