3.1.3 Пилообразный сигнал

Рисунок 3 — Пробный пилообразный сигнал и его спектр

Вызвав функцию signal.sawtooth(), мы построим нужный нам сигнал и его спект

sig_saw = test_sig_ampl ∗ s i g n a l . sawtooth ( t ∗ 2 ∗ np . pi ∗ test_sig_freq)

sig_saw_spec = np . abs ( np . f f t . f f t ( sig_saw ) ) saw_freqs = np . f f t . f f t f r e q ( sig_saw . shape [ 0 ] , dt )

Дальше построим графики, аналогично как мы строили для синуса и меандра.

2. Реле

Теперь мы рассмотрим Реле на трёх видах пробных сигналов.

1. Синусоида

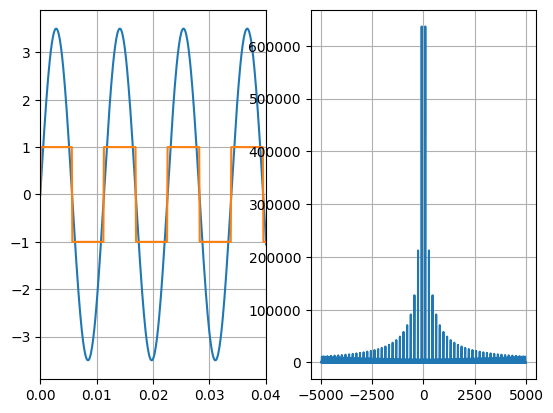
Рисунок 4 — Синус через реле и спектр выходного сигнала

Вызываем функцию из библиотеки numpy, np.sign. Синус проходит через Реле

s i g_sin_relay = np . s i g n ( s i g _si n )

s i g_sin_relay_spectre = np . abs ( np . f f t . f f t ( s i g_sin_relay ) )

s i g_sin_relay_freqs = np . f f t . f f t f r e q ( s i g_sin_relay . shape [ 0 ] ,dt)

Построим график сигнала с изменениями и без, чтобы лучше увидеть изменения

p l t . subplot ( 1 , 2 , 1 ) p l t . g r i d ( )

−

p l t . ylim ( 1 .9 , 1 . 9 ) p l t . xlim ( 0 , 0.2 )

p l t . p l o t ( t , s ig_sin , t , s i g_sin_relay ) p l t . subplot ( 1 , 2 , 2 )

p l t . g r i d ( )

p l t . p l o t ( s ig_sin_relay_freqs , s i g_sin_relay_spectre )

мы можем увидеть, что после прохождения данного звена, синус становится похожим на меандр, с амплитудой равно 1 и частотой равно частоте синуса.

2. Меандр

Рисунок 5 — Меандр через реле и спектр выходного сигнала

Здесь мы рассмотрим прохождения меандра через реле. Используем ту же функцию что и в части, написанной выше.

s ig_square_relay = np . s i g n ( s ig_square )

s ig_square_relay_spec = np . abs ( np . f f t . f f t ( s ig_square_relay ) ) s ig_square_relay_freqs = np . f f t . f f t f r e q ( s ig_square_relay . shape

можем заметить, что форма сигнала не меняется, а амплитуда выходного сигнала становится равной 1.

3. Пилообразный сигнал

Рисунок 6 — Пилообразный сигнал через реле и спектр выходного сигнала

Используем те же функции.

sig_saw_relay = np . s i g n ( sig_saw )

sig_saw_relay_spec = np . abs ( np . f f t . f f t ( sig_saw_relay ) ) s ig_saw_relay_freqs = np . f f t . f f t f r e q ( sig_saw_relay . shape [ 0 ] , d

Пилообразный сигнал заменился меандром с амплитудой равной 1, а также сжался по частоте. Так же его спектр не отличается от спектров синуса и меандра.

3. Мертвая зона

Реализация звена в Python:

−

def dead_zone_scalar ( x , wight = 0 . 5 ) :

i f np . abs ( x ) < wight :

return 0 e l i f x > 0 :

e l s e :

return x − wight return x + wight

dead_zone = np . v e c t o r i z e ( dead_zone_scalar , otypes = [ np . f l o a t ],

excluded = [‘width’])

1. Синусоида

Рисунок 7 — Синус через мертвую зону и спектр выходного сигнала

Ниже мы уже привели код для реализации мертвой зоны.

Теперь мы будем использовать его с нелинейным параметром, который вычисляется по формуле 0.5 + вариант * 0.1. Для нашего случая, параметр равен 1.

sig_sin_dz = dead_zone ( s ig_sin , non_lin_param_1 )

sig_sin_dz_spec = np . abs ( np . f f t . f f t ( sig_sin_dz ) ) s ig_sin_dz_freqs = np . f f t . f f t f r e q ( sig_sin_dz . shape [ 0 ] , dt )

Теперь построим графики входного и выходного сигнала

Амплитуда сигнала изменилась и появилась зона, в которой сигнал становится равным нулю. Амплитуда уменьшилась на 1, т.е. на коэффициент нашего нелинейного звена.

2. Меандр

Рисунок 8 — Меандр через мертвую зону и спектр выходного сигнала

В этой секции мы рассмотрим прохождения меандра через мертвую зону. Используем вышеописанный алгоритм для имитации прохождения сигнала через мертвую зону и используем выше посчитанный коэффициент.

sig_square_dz = dead_zone ( sig_square , non_lin_param_1 ) sig_square_dz_spec = np . abs ( np . f f t . f f t ( sig_sin_dz ) )

sig_square_dz_freqs = np . f f t . f f t f r e q ( sig_sin_dz . shape [ 0 ] , dt )

Амплитуда сигнала уменьшилась на 1 как и у синуса.