МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра АПУ

ОТЧЕТ

по лабораторной работе №1

по дисциплине «Теория автоматического управления» Тема: Типовые нелинейности

Студент гр. 0391 Чащин Д. Преподаватель К.М. Жеронкин

Санкт-Петербург 2023

Содержание

1. Задача работы

2. Задание на лабораторную работу

3. Отчет по лабораторной работе

3.1 Пробные сигналы

3.1.1 Синусоида

3.1.2 Меандр

3.1.3 Пилообразный сигнал

3.2 Реле

3.2.1 Синусоида

3.2.2 Меандр

3.2.3 Пилообразный сигнал

3.3 Мертвая зона

3.3.1 Синусоида

3.3.2 Меандр

3.3.3 Пилообразный сигнал

3.4 Насыщение

3.4.1 Синусоида

3.4.2 Меандр

3.4.3 Пилообразный сигнал

4. СХ нелинейных звеньев в Simulink

3.4.1 Прохождение сигнала через Реле

3.4.2 Прохождение сигнала через Мертвую зону

3.4.3 Прохождение сигнала через Насыщение

5. Вывод

Лабораторная работа 1. Типовые нелинейности в моделях систем управления

Добавление нелинейных элементов (НЭ) - распространенная практика в создании нелинейных моделей систем управления. Такие элементы позволяют учесть ряд естественных факторов, таких как ограничения на управляющие воздействия, зоны нечувствительности в измерительных и исполнительных механизмах, наличие люфта в кинематических сочленениях и прочее. Вбудовывание таких НЭ в линейные модели систем управления значительно повышает их эффективность и точность.

Задача работы:

Изучение типовых НЭ моделей систем автоматического управления.

Задание на лабораторную работу:

Для безынерционных НЭ типа «идеальное реле», «зона нечувствительности», «насыщение»:

• сгенерировать различные тестовые (пробные) сигналы;

• получить реакции НЭ на тестовые сигналы;

- построить статические характеристики (СХ) НЭ;

• по СХ НЭ объяснить разницу в реакциях при разных пробных сигналах.

3. Отчет по лабораторной работе

1. Пробные сигналы

   1. Синусоида

В данном разделе мы рассмотрим тестовый сигнал в виде синусоиды. В соответствии с заданием нам необходимо было сформировать сигнал с амплитудой, вычисляемой по формуле: 1 + вариант * 0.1, и частотой, вычисляемой следующим образом: 1 + вариант * 3.5. Учитывая наш вариант, мы получаем значения амплитуды, равной 1.5, и частоты, равной 18.5. Рассмотрим, как можно сформировать данный сигнал с использованием языка программирования Python.

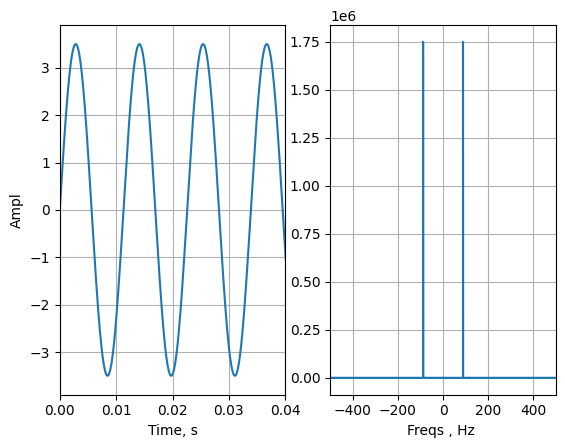
Рисунок 1 — Пробный сигнал синуса и его спектр

t = np.arange(0, test_signal_duration, dt)

sig_sin = test_sig_ampl * np.sin(t*2*np.pi*test_sig_freq);

Формируем синусоидальный сигнал с нужными нам частотой и амплитудой. Потом построим спектр нашего сигнала.

s ig_sin_spec = np . abs ( np . f f t . f f t ( s i g_s in ) )

s i n _f r e q s = np . f f t . f f t f r e q ( s i g_s in . shape [ 0 ] , dt )

Теперь построим графики.

p l t . subplot ( 1 , 2 , 1 ) p l t . g r i d ( )

p l t . x l a b e l ( ’ Time , s ’ ) p l t . y l a b e l ( ’ Ampl ’ )

−

p l t . ylim ( 1 .9, 1 . 9 ) p l t . xlim ( 0 , 0. 2 )

p l t . p l o t ( t , s i g _s i n ) p l t . subplot ( 1 , 2 , 2 )

p l t . g r i d ( )

−

p l t . x l a b e l ( ’ Freqs , Hz ’ ) p l t . xlim ( 55 , 55 )

p l t . p l o t ( s in_freqs , s ig_sin_spec )

p l t . show ( )

3.1.2 Меандр

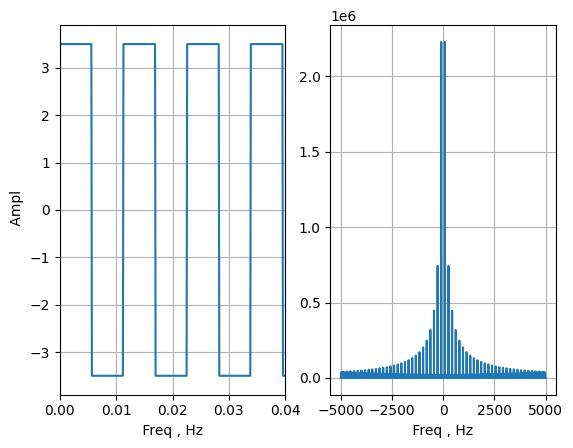
Рисунок 2 — Пробный сигнал меандра и его спектр

Рассмотрим построение меандра с использованием языка программирования Python. Наша задача - создать меандр с амплитудой, равной 1.5, и частотой, равной 18.5 Гц. Для этого мы будем использовать библиотеку Python:

from s c i p y import s i g n a l

Вызвав функцию signal.square, мы строим сигнал и его спектр.

s ig_square = test_sig_ampl ∗ s i g n a l . square ( t ∗ 2 ∗ np . pi * test_sig_freq)

sig_square_spec = np . abs ( np . f f t . f f t ( s ig_square ) ) square_freqs = np . f f t . f f t f r e q ( s ig_square . shape [ 0 ] , dt )

Построим графики спектра и самого сигнала.

p l t . subplot ( 1 , 2 , 1 ) p l t . g r i d ( )

−

p l t . y l a b e l ( ’ Ampl ’ ) p l t . ylim ( 1 .9 , 1 . 9 )

p l t . x l a b e l ( ’ Freq , Hz ’ ) p l t . xlim ( 0 , 0.2 )

p l t . p l o t ( t , s ig_square )

p l t . subplot ( 1 , 2 , 2 ) p l t . g r i d ( )

p l t . x l a b e l ( ’ Freq , Hz ’ )

p l t . p l o t ( square_freqs , sig_square_spec )

p l t . show ( )