ЛАБЫ / TAulaba5

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра АПУ

отчет

по лабораторной работе №5

по дисциплине «Теория автоматического управления»

Тема: Анализ устойчивости положения равновесия

Студенты гр. 0391		Варик А.Ю. Чащин Д. Ломаков Д.М.
Преподаватель		Жеронкин К.М.

Санкт-Петербург

2023

Основные теоретические положения

Первый метод Ляпунова позволяет судить об устойчивости изолированного положения равновесия по линеаризованным уравнениям. Метод основан на утверждениях:

• если собственные значения (с.з.) линеаризованной системы имеют отрицательные действительные части (линеаризованная система асимптотически устойчива), то положение равновесия нелинейной системы устойчиво «в малом»;

• если среди с.з. линеаризованной системы имеются «правые», то положение равновесия нелинейной системы неустойчиво;

• если имеются некратные с.з. на мнимой оси, а остальные — «левые», то в этом критическом случае по линеаризованной модели нельзя судить об устойчивости положения равновесия нелинейной системы.

Пример исследования устойчивости положения равновесия

осциллятора Ван дер Поля, описываемого дифференциальным уравнением второго порядка:

.

Система имеет единственное положение равновесия 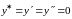. Линеаризованное для малых отклонений уравнение запишется так:

,

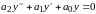где:

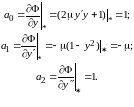
Характеристический полином уравнения

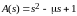
имеет следующие корни

.

Положение равновесия не устойчиво, если  > 0. При значении   2 на фазовой плоскости в начале координат имеется особая точка типа «неустойчивый узел». При значениях 0 <  < 2 имеет место особая точка типа «неустойчивый фокус».

Фазовый портрет осциллятора Ван дер Поля имеет устойчивый предельный цикл, которому соответствуют автоколебания в нелинейной системе (см. Лабораторную работу 4).

Задание 1. Проанализируйте первым методом Ляпунова нелинейный осциллятор, заданный системой дифференциальных уравнений.

;

.

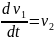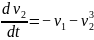Найдите координаты положения равновесия: из условий

.

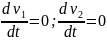Применение первого метода Ляпунова

Пусть переменных малы. Тогда в исходных уравнениях состояния можно пренебречь членом  , в результате чего получим линейные уравнения:

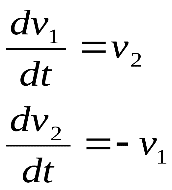
Запишем систему уравнений состояния в матричной форме:

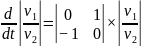
Характеристический полином матрицы А

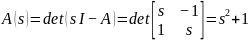
Корни характеристического полинома

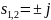
Т.е. корни находятся на границе устойчивости. Таким образом, первый метод Ляпунова не позволяет сказать что-то об устойчивости положения равновесия, т.к. неизвестно, как действует член, которым мы пренебрегли на расположение полюсов.

Второй метод Ляпунова.

Второй метод Ляпунова не связан с линеаризацией. Выберем положительно – определенную функцию:

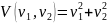
Найдем производную этой функции по времени:

В силу дифф. уравнений системы, имеем:

Функция   обращается в ноль в точке равновесия (0).

Получили отрицательную знакпостоянную функцию, следовательно, положение равновесия устойчиво.

Построим фазовый портрет нелинейного осциллятора на языке программирования Python.

import numpy as np

import matplotlib.pyplot as plt

# функция правых частей системы

def f(t, v):

    dv1dt = v[1]

    dv2dt = -v[0] - v[1]**3

    return np.array([dv1dt, dv2dt])

# создаем сетку для построения фазового портрета

v1 = np.linspace(-2, 2, 20)

v2 = np.linspace(-2, 2, 20)

V1, V2 = np.meshgrid(v1, v2)

# вычисляем значения производных на сетке

DV1DT, DV2DT = f(0, [V1, V2])

# рисуем фазовый портрет

plt.streamplot(V1, V2, DV1DT, DV2DT)

plt.xlabel('$v_1$')

plt.ylabel('$v_2$')

plt.title('Фазовый портрет нелинейного осциллятора')

plt.show()

Получим следующий график

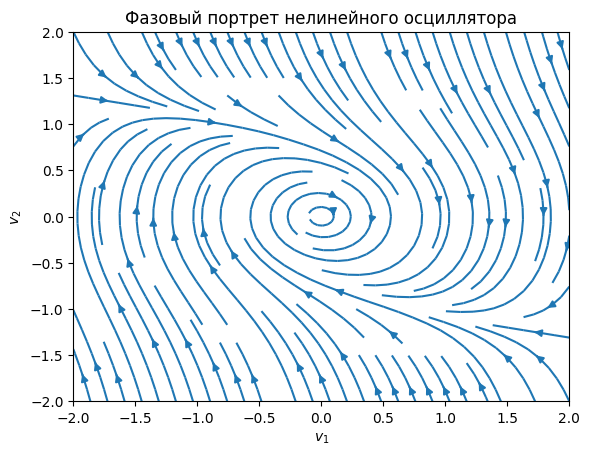
Что можно сказать об устойчивости положения равновесия?

На графике фазового портрета нелинейного осциллятора не видно положения равновесия. Это свидетельствует о том, что система имеет устойчивые положения равновесия.

Задание 2. Проанализируйте первым методом Ляпунова систему, заданную структурной схемой

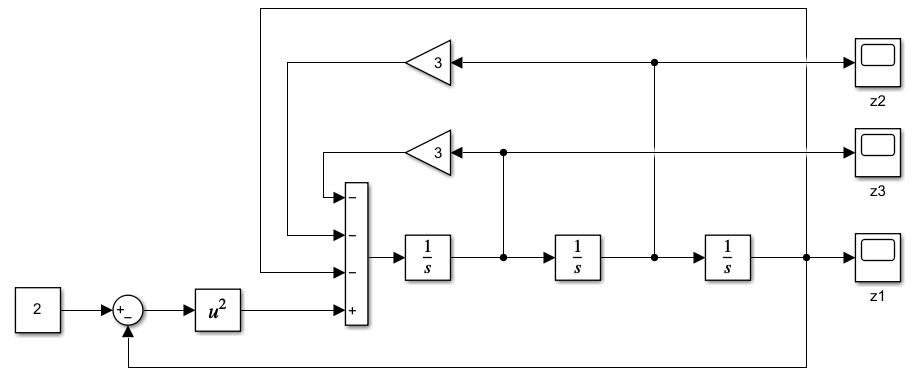
Рис. 5.1. Структура модели

Составим систему дифференциальных уравнений.

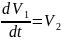
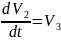
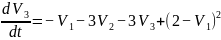
1. Найдем положение равновесия, для этого нужно решит систему уравнений, приравняв производные к нулю.

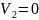
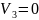
В таком случае

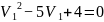
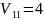
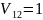
В тако случае положение равновесия в точках (1,0, 0) и (4,0,0)

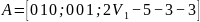- матрица состояний линеаризованной системы.

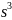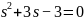ХП: +3 в точке (1,0,0)

Корни

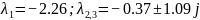
Устойчивое положение равновесия

ХП: +3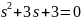 в точке (1,0,0)

Корни

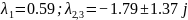
Неустойчивое положение равновесия

Вывод. В данной лабораторной работе мы научились анализировать системы методом Ляпунова, а также анализировать устойчивость положения равновесия системы.