
Система 1

def ode(Y, t):
x, y = Y
dydt = [ -4*x + 0.1*(x**2) - 4*y, 1.5*x + y - 0.2*(y**3) ]
return dydt
drawPhasePortrait(-2, 2,-2, 2, 1,1, -3,4, -3,3, ts =1.5, nt =201)
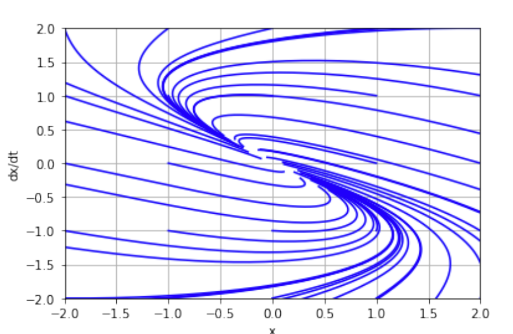 Система
1
Система
1
Для линеаризации системы нужно разложить нелинейные функции в ряд Тейлора до первого порядка в окрестности некоторой точки (x0, y0). Выберем точку (0, 0):
f(x, y) = -4x + 0.1x^2 - 4y
f(0, 0) = 0
∂f/∂x(0, 0) = -4
∂f/∂y(0, 0) = -4
g(x, y) = 1.5x + y - 0.2y^3
g(0, 0) = 0
∂g/∂x(0, 0) = 1.5
∂g/∂y(0, 0) = 1
Подставляя эти значения в линейную систему, получим:
x' = -4x - 4y
y' = 1.5x + y
Линеаризованная система

def ode(Y, t):
x, y = Y
dydt = [ -4*x - 4*y, 1.5*x + y]
return dydt
drawPhasePortrait(-2, 2,-2, 2, 1,1, -3,4, -3,3, ts =1.5, nt =201)
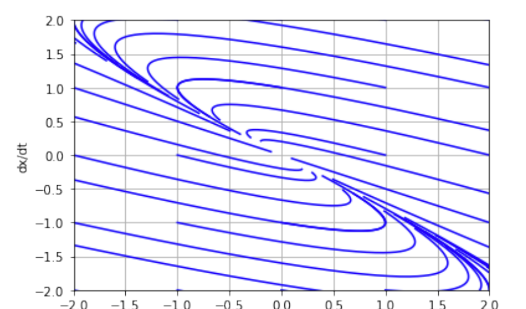
Фазовый портрет имеет вид особой точки «неустойчивый узел». Система имеет положительные действительные корни. Фазовый портрет линеаризованной модели практически не отличается от первоначальной. Положение равновесия неустойчиво
Система 2

def ode(Y, t):
x, y = Y
dydt = [ x + 0.5*y - 0.1 * (y**2), 0.5*x + y - 0.2*(x**2)+y]
return dydt
drawPhasePortrait(-5, 5,-5, 5, 1,1, -7,7, -7,7, ts =1.5, nt =300)
 Система
2
Система
2
Линеаризованная система

def ode(Y, t):
x, y = Y
dydt = [ x + 0.5*y, 0.5*x + y]
return dydt
drawPhasePortrait(-5, 5,-5, 5, 1,1, -7,7, -7,7, ts =1.5, nt =300)
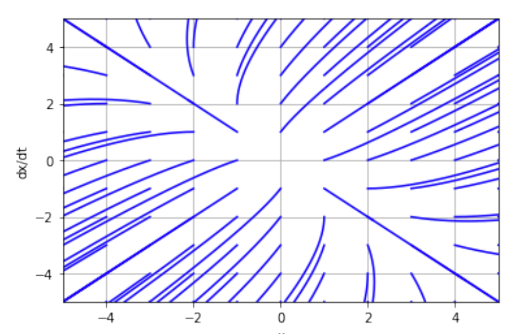
Фазовый портрет имеет вид особой точки «устойчивый узел». Система имеет отрицательные действительные корни. Положение равновесия не линеаризованной системы не устойчиво.
Система 3

def ode(Y, t):
x, y = Y
dydt = [ 2*x + 0.2*(x**2) + y - 0.1*(y**2), x - 3*y ]
return dydt
drawPhasePortrait(-4, 7,-4, 4, 1,1, -10,5, -10,10, ts =0.29, nt =301)
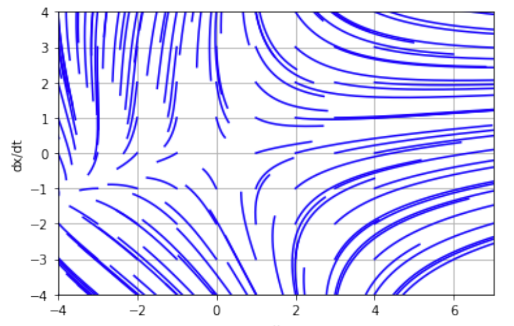 Система
3
Система
3
Линеаризованная система

def ode(Y, t):
x, y = Y
dydt = [ 2*x + y, x - 3*y ]
return dydt
drawPhasePortrait(-4, 7,-4, 4, 1,1, -10,5, -10,10, ts =0.29, nt =301)
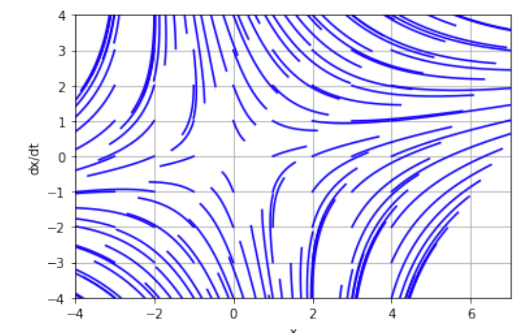
Фазовый портрет имеет вид особой точки «седло». Система имеет положительные и отрицательные действительные корни. Фазовый портрет линеаризованной модели практически не отличается от первоначальной. Положение равновесия неустойчиво.
Система 4

def ode(Y, t):
x, y = Y
dydt = [ -0.1*(x**2) + 2*y, -3*x - y ]
return dydt
drawPhasePortrait(-5, 4,-5, 5, 1,1, -5,5, -5,5, ts =0.6, nt =201)
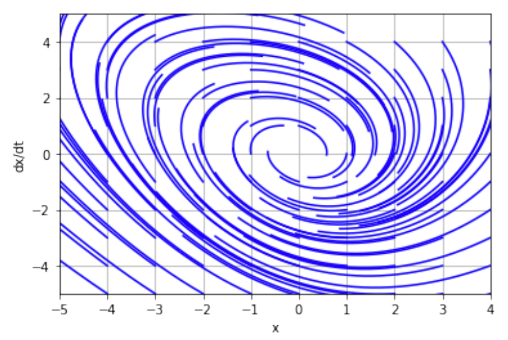 Система
4
Система
4
Линеаризованная система

def ode(Y, t):
x, y = Y
dydt = [ 2*y, -3*x - y ]
return dydt
drawPhasePortrait(-5, 4,-5, 5, 1,1, -5,5, -5,5, ts =0.6, nt =201)
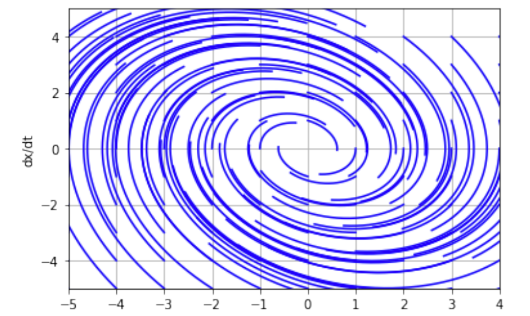
Фазовый портрет имеет вид особой точки «устойчивый фокус». Система имеет комплексно-сопряженные с отрицательными действительными частями. Фазовый портрет линеаризованной модели практически не отличается от первоначальной. Положение равновесия малоустойчиво.
Система 5

def ode(Y, t):
x, y = Y
dydt = [ 0.1*x - 4*y, 4*x - 0.2*(x** 2) + 0.1*y ]
return dydt
drawPhasePortrait(-6, 5,-7, 7,5, 1,1, -10,10, -10,10, ts =0.2, nt =201)
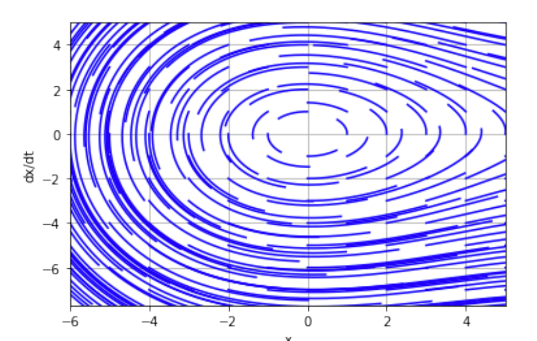 Система
5
Система
5
Линеаризованная система

def ode(Y, t):
x, y = Y
dydt = [ 0.1*x - 4*y, 4*x + 0.1*y ]
return dydt
drawPhasePortrait(-6, 5,-7, 7,5, 1,1, -10,10, -10,10, ts =0.2, nt =201)
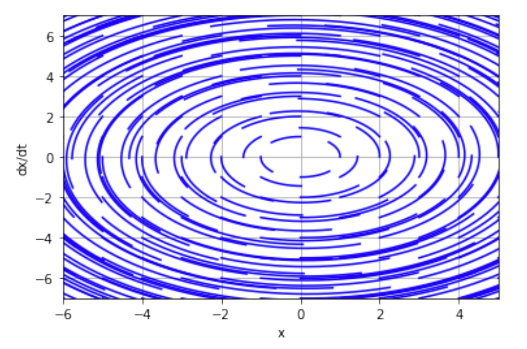
Фазовый портрет имеет вид особой точки «неустойчивый фокус». Система имеет комплексные корни с положительной действительной частью. Фазовый портрет линеаризованной модели практически не отличается от первоначальной. Положение равновесия неустойчиво
