LR1_MOTS

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра АПУ

отчет

по лабораторной работе №1

по дисциплине «Математические основы теории систем»

Тема: Матричные преобразования и трехмерная графика

Студенты гр. 0391		Абрамова А.К.
		Чащин Д.
		Филиппова А.С.
Преподаватель		Гульванский В.В.

Санкт-Петербург

2022

Цель работы: освоение специфики матричных преобразований MATLAB и сравнительный анализ различных форм графического отображения результатов.

Ход работы:

В начале работы использовались команды, отчищающие командную строку (clc), закрывающее ненужные окна(close all) и удаляющие неиспользуемые переменные(clear).

clc;

clear all;

clf;

Задание 1. В качестве исходной фигуры, на которой будем изучать матричные преобразования, выберем пирамиду (рис. 1). Симметрия матрицы R относительно главной диагонали и антидиагонали делает такую матрицу вырожденной – ее определитель равен нулю. Соответственно, большинство матричных операций для нее невыполнимо. Поэтому добавим к элементам на главной диагонали по единице, сложив ее с единичной матрицей (eye) того же размера. Теперь над матрицей можно производить как поэлементные, так и матричные операции.

Для построения пирамиды формируем 2 взаимно перпендикулярные плоскости Х и Y – аналоги двумерных осей ординат.

x = -10:10;

y = ones(1,21);

X = x'*y;

Y = y'*x;

И построим пирамиду (рис. 1).

R = max(abs(X),abs(Y));

figure(1);

surf(X,Y,-R);

title('Исходная пирамида')

Проверяем что определитель равен 0

det_R=det(R);

Так как det_R = 0, большинство матричных операций для нее невыполнимо. Поэтому добавим к элементам на главной диагонали по единице, сложив ее с единичной матрицей (eye) того же размера. Теперь над матрицей можно производить как поэлементные, так и матричные операции.

R=R+eye(21);

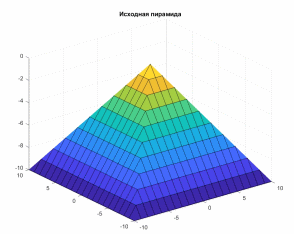
Рис. 1

Задание 2. Сравните (по графикам - рис.2) результаты двух операций – обращения матрицы командой inv и поэлементного деления матрицы ones(n,n) на R.

figure(2);

inv_R=inv(R);

S = ones(size(R))./R;

subplot(1, 2, 1),surf(X,Y,-inv_R);

title('Обращение матрицы командой inv')

subplot(1, 2, 2), surf(X,Y,-S);

title('Поэлементного деления матрицы')

После построения двух графиков (рис. 2), можем сделать вывод, что графики не идентичны.

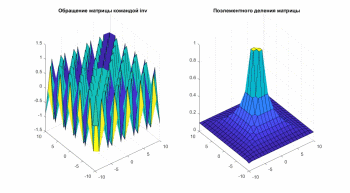
Рис. 2

Задание 3. Сравните матричные операции sqrtm(A), logm(A), expm(A) с аналогичными операциями, выполняемыми поэлементно.

Операция sqrtm()

Сравнение производится построением двух графиков (рис. 3).

figure(3);

R_sqrtm= sqrtm(R);

subplot(1, 2, 1),surf(X,Y,abs(R_sqrtm));

title('Матричная операция sqrtm(R)')

R_sqrtm_el=R.^(1/2);

subplot(1, 2, 2),surf(X,Y,R_sqrtm_el);

title('Поэлементное выполнение операции sqrtm')

После построения двух графиков (рис. 3), можем сделать вывод, что графики не идентичны.

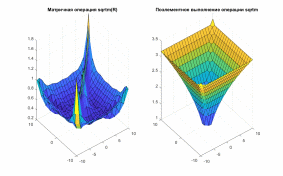
Рис. 3

Операция logm()

Сравнение производится построением двух графиков (рис. 4).

figure(4);

R_log=logm(R)

subplot(1, 2, 1),surf(X,Y,abs(R_log)); title('Матричная операция logm(R)')

R_logPoel=log(R);

subplot(1, 2, 2),surf(X,Y,abs(R_logPoel));

title('Поэлементное выполнение операции logm')

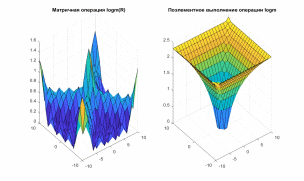
Рис. 4

После построения двух графиков (рис. 4), можем сделать вывод, что графики не идентичны.

Операция expm()

Сравнение производится построением двух графиков (рис. 5).

figure(5);

R_exp=expm(R);

subplot(1, 2, 1),surf(X,Y,R_exp);

title('Матричная операция expm(R)')

R_expPoel=exp(R);

subplot(1, 2, 2), surf(X,Y,R_expPoel);

title('Поэлементное выполнение операции expm')

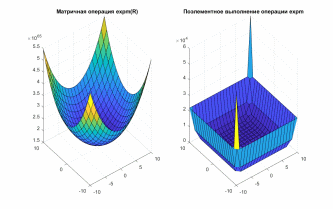
Рис. 5

После построения двух графиков (рис. 5), можем сделать вывод, что графики не идентичны.

Задание 4. Преобразуйте пирамиду R операциями врезки. «Отрежьте» один из углов, приравняв нулю выбранные элементы.

R1 = R;

R1(:,1:5)=0; figure(6)

mesh(R1)

R1(10:15,:)=4; figure(7)

mesh(R1)

surfl(R1) % освещенная поверхность (без каркасной сетки)

shading interp % линейное изменение цвета

colormap('gray') % палитра серого

Результаты приведены в виде графиков (рис. 6 и рис. 7).

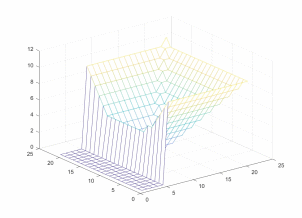
Рис. 6

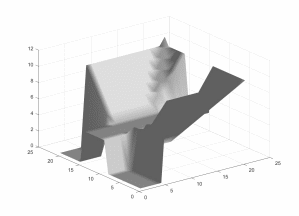
Рис. 7

Задание 5. Создайте 9 конусов c помощью матрицы 3*3. Поменяйте порядок матриц в последней операции (рис. 8). Сделайте Центральный конус в два раза выше соседей.

figure(8);

Cone=sqrt(X.^2+Y.^2);

Unit=ones(3,3);

Kron_cone=kron(Unit,Cone);

Kron_cone2=kron(Cone,Unit);

subplot(1, 2, 1),surf(-Kron_cone);

xlabel('Координата Х');

ylabel('Координата Y');

title('Кронекеровское умножение матриц');

subplot(1, 2, 2), surf(-Kron_cone2);

title('Кронекеровское умножение матриц со сменой порядка');

xlabel('Координата Х');

ylabel('Координата Y');

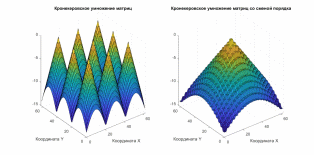
Рис. 8

Сделаем центральный конус в два раза выше соседей (рис. 9)

figure(9);

Kron_cone3=kron(Unit,Cone);

Kron_cone3(21:42,21:42)=Kron_cone3(21:42,21:42)-7;

surf(-Kron_cone3);

xlabel('Координата Х');

ylabel('Координата Y');

title('Кронекеровское умножение матриц(Центральный конус в 2 раза выше');

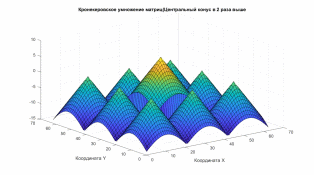
рис. 9

Задание 6. На основе данных из пункта 5 создайте две картинки с помощью функций heatmap и imagesc, установите границы сегментации данных. Сравните полученные результаты. Уберите «сетку», чтобы данные графики были более репрезентативны.

Создание тепловой карты с помощью heatmap (рис. 10)

figure(10);

h1 = heatmap(-Kron_cone);

grid off;

h1.Title = 'Тепловая карта 9 Конусов';

h1.XLabel = 'Х координата';

h1.YLabel = 'Y координата';

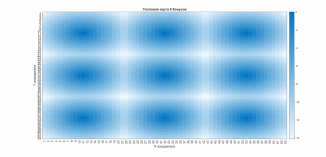
Рис. 10

Создание тепловой карты с помощью imagesc (рис. 11)

figure(11);

h2=imagesc(-Kron_cone);

grid off;

colorbar;

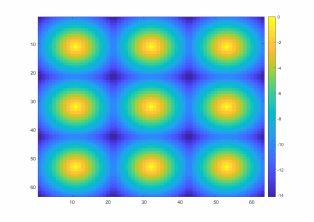
Рис. 11