lr4

МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра АПУ

ОТЧЕТ по лабораторной работе №4

по дисциплине «Математические основы теории систем» Тема: Дискретные системы

Санкт-Петербург

2022

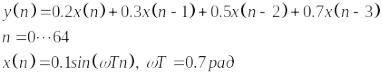
Цель работы:

•Знакомство с дискретными системами и операцией дискретной свертки;

•Расчет импульсной и частотных характеристик;

•Изучение визуальных средств проектирования цифровых фильтров;

Ход работы:

В начале работы использовались команды, отчищающие командную строку (clc), закрывающее ненужные окна (close all) и удаляющие неиспользуемые переменные (clear).

clc; %очистка командного окна

close all; % закрывает все окна

clear; % удаляет все переменные из рабочей области

Задание 1. Рассчитать реакцию КИХ-фильтра 3-го порядка, заданного разностным уравнением:

% Задание 1

b= [0.2 0.3 0.5 0.7]; a = [1];

n = 0 : 64;

x = 0.1 * sin (0.7 * n); y=filter (b,a,x);

figure('name' , 'Signals "КИХ"'); plot (n,x,n,y,'--'),grid title("Signals");

xlabel (['n']) ylabel (['signal'])

legend('входной сигнал', 'выходной сигнал') hold on

2

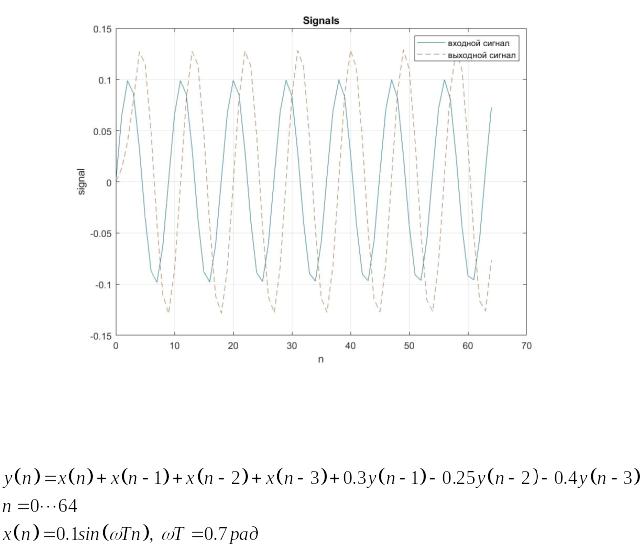
Рис. 1

Задание 2. Рассчитать реакцию БИХ-фильтра 3-го порядка, заданного разностным уравнением:

% Задание 2 b = [1 1 1 1];

a = [1 -0.3 0.25 0.4]; n = 0 : 64;

x = 0.1 * sin (0.7 * n); y=filter (b,a,x);

figure('name' , 'Signals "БИX"'); plot (n,x,n,y,'--'),grid title("Signals");

xlabel (['n']) ylabel (['signal'])

legend('входной сигнал', 'выходной сигнал') hold on

3

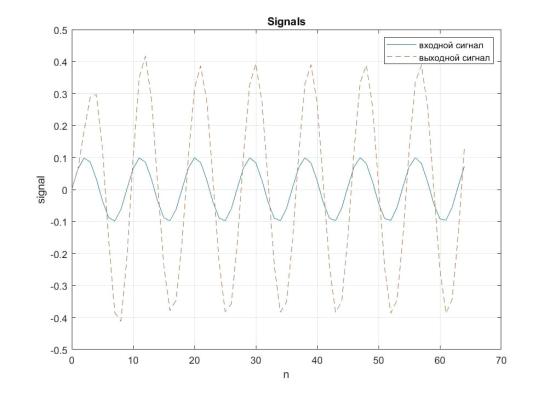
Рис. 2

Задание 3. Вычислить импульсную характеристику БИХ-фильтра, заданного

впункте № 2.

%Задание 3

b= [1 1 1 1];

a = [1 -0.3 0.25 0.4]; n = 0 : 64;

c = zeros(1, 64); c(1) = 1; y=filter (b,a,c);

figure('name' , 'Импульсная характеристика'); plot (y), grid

title("impulsnay"); xlabel (['n'])

ylabel (['импульсная характеристика БИХ-фильтра']) legend('импульсная характеристика')

hold on

4

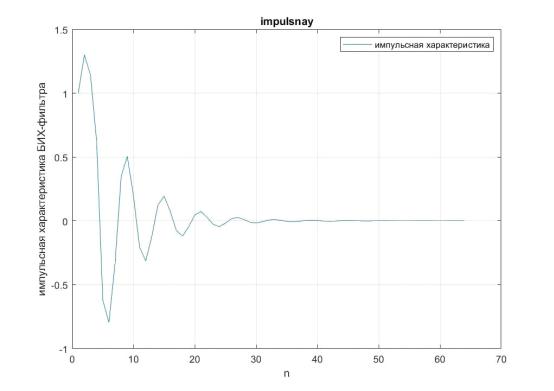
Рис. 3

Задание 4. Вычислить импульсную характеристику БИХ-фильтра, заданного в пункте No 2, используя функцию impz(), при N = 80, Fs = 5000 Гц.

% Задание 4

y = impz(b, a, 80, 5000);

figure('name' , 'Импульсная характеристика'); plot (y), grid

title("impulsnay"); xlabel (['n'])

ylabel (['импульсная характеристика БИХ-фильтра (2)']) legend('импульсная характеристика')

hold on

5

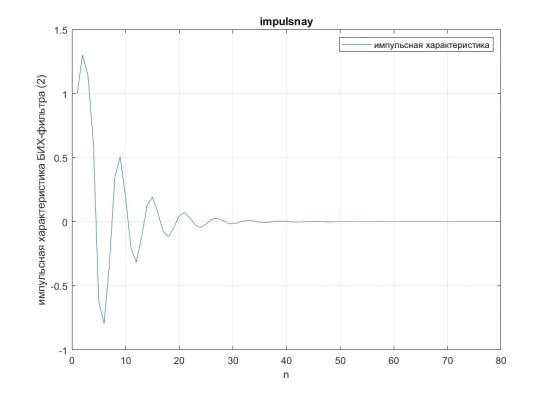
Рис. 4

Задание 5. Используя утилиту fdatool синтезировать полосовой КИХ-фильтр со следующими параметрами (нормированная полоса частот):

•полоса пропускания 0,35-0,7;

•полоса задерживания 0-0,15 0,8-1;

•неравномерности по 0,025 в ПП и ПЗ; Получить ИХ, АЧХ и ФЧХ фильтра.

Синтезировали КИХ-фильтр со следующими настройками (Рис. 5):

6

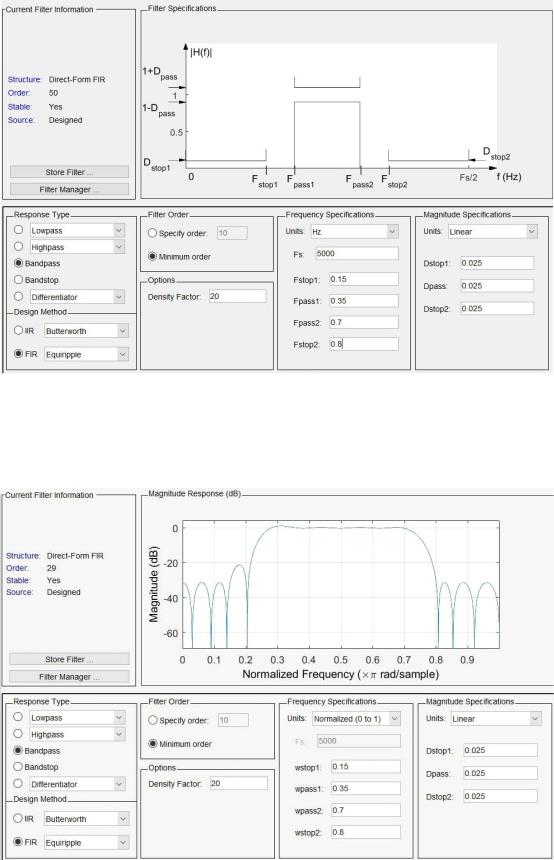
Рис. 5

АЧХ, ФЧХ и ИХ представлены на Рис. 6, Рис.7, Рис. 8 соответственно.

Рис. 6

7

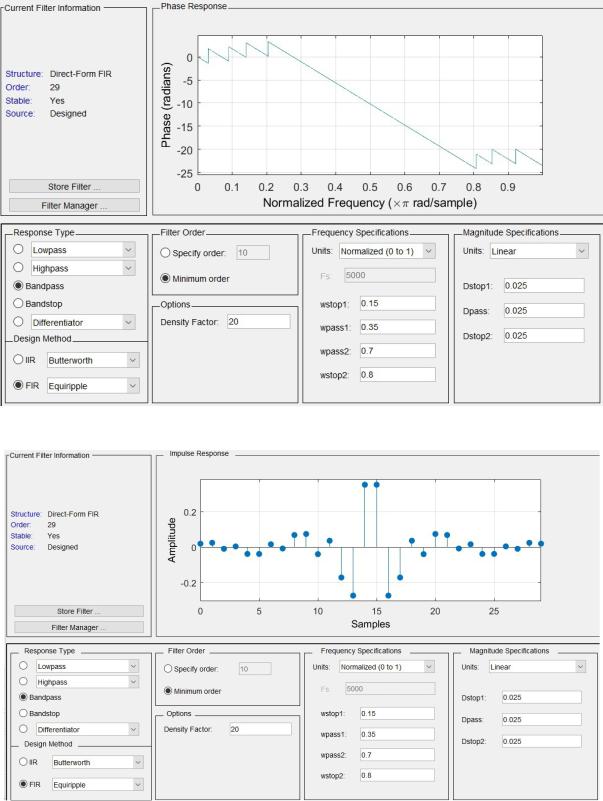
Рис. 7

Рис. 8

Задание 6. По заданному набору коэффициентов КИХ-фильтра получить его АЧХ, ФЧХ и ИХ

8

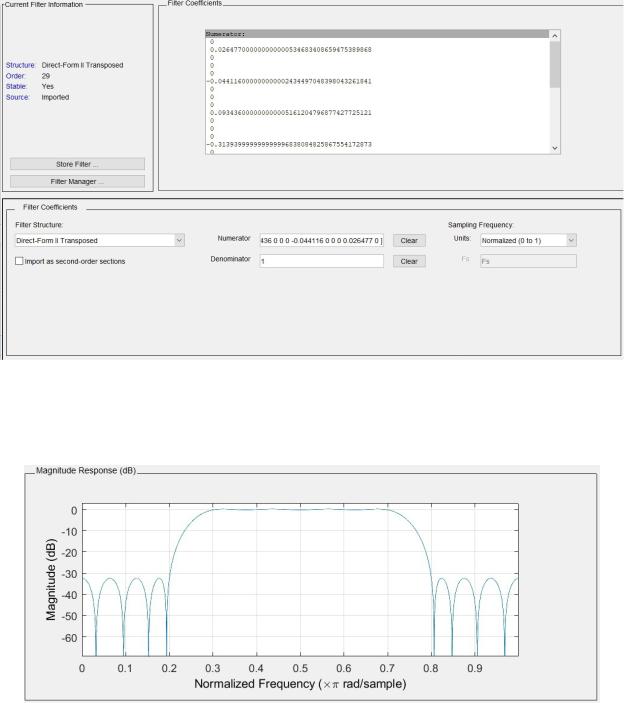
[0 0,026477 0 0 0 -0,044116 0 0 0 0,093436 0 0 0 -0,31394 0 0,5 0 -0,31394 0 0 0 0,093436 0 0 0 -0,044116 0 0 0 0,026477 0]

Строим КИХ-фильтр по заданным коэффициентам (Рис. 9)

Рис. 9

АЧХ, ФЧХ и ИХ данного фильтра представлены на Рис. 10, Рис.11, Рис. 12 соответственно.

Рис. 10

9

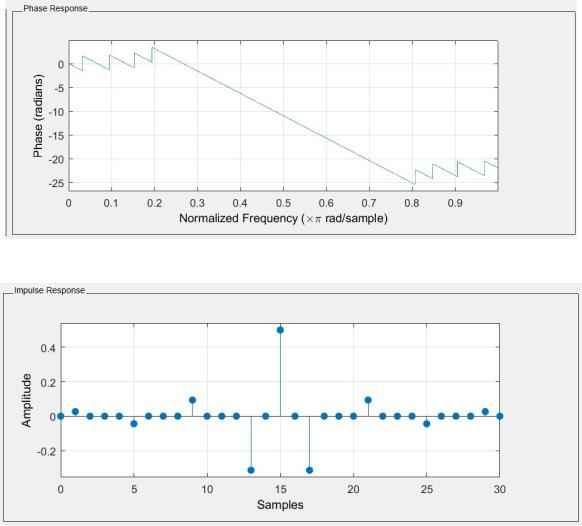
Рис. 11

Рис. 12

Вывод: в ходе лабораторной работы мы ознакомились с дискретными системами и операцией дискретной свертки; рассчитали импульсную и частотную характеристики; изучили визуальные средства проектирования цифровых фильтров.

10