
Lab1_TOE_Chashchin_0391
.pdfМИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
Кафедра «ТОЭ»
ЛАБОРАТОРНАЯ РАБОТА по дисциплине «ТОЭ»
Тема: «ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ РЕЗИСТИВНЫХ ЦЕПЕЙ»
Студент гр. 0391 |
|
Чащин Д. |
|
Преподаватель |
|
|
Езеров К.С |
Санкт-Петербург
2022
Цель работы:
Экспериментальное исследование линейных разветвленных резистивных цепей с использованием методов наложения, эквивалентного источника и принципа взаимности.
Протокол:
№ ветви |
|
1 |
|
|
2 |
|
3 |
|
4 |
|
Uk, В |
0,731 |
|
|
|
-0,906 |
|
3,269 |
4,175 |
||
Ik, мА |
0,487 |
|
|
|
0,604 |
|
1,093 |
1,395 |
||
|
Табл.1 - цепь при питании ее от двух источников |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Источники |
|
|
1 |
|
|
2 |
|
3 |
|
4 |
U=4 В; I=0 мА |
I‘k |
|
1.214 |
|
-0.486 |
|
0.729 |
|
0.486 |
|
U=0 В; I=2 мА |
I‘’k |
|
-0.726 |
|
1.090 |
|
0.364 |
|
0.910 |
|
U=4 В; I=2 мА |
Ik |
|
|
|
|
|
|
|
|
|
|
Табл.2 – цепь, рассчитанная методом наложения |
|
|
|||||||
3.1.
0 = 4.479
3.2
0 = 4,490 В - 3 = −1.092
4.1
3 = 0,729 А
4.2
1 = 0.731 .
Ход работы.
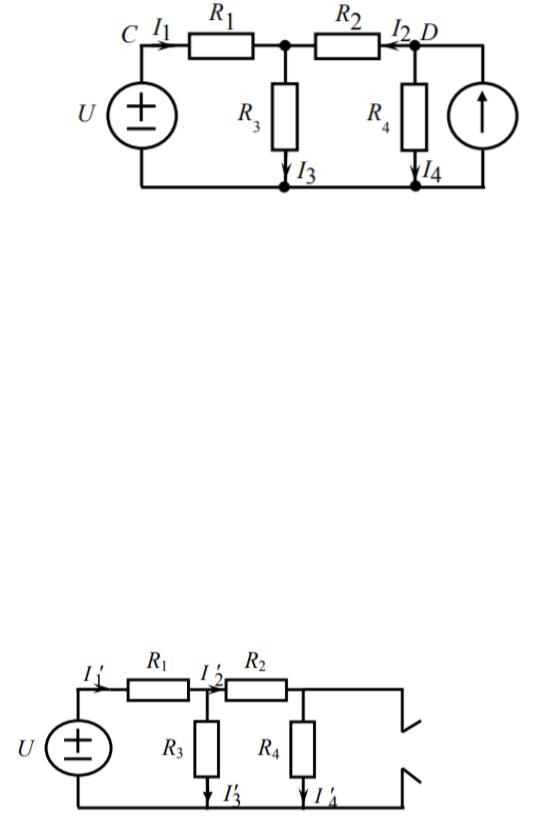
1) Исследование цепи при питании ее от двух источников
Рисунок 1 – Схема с двумя источниками
Рассчитаем токи и напряжения на резисторах при двух источников по закону Кирхгофа.
По первому закону Кирхгофа
{ 1 + 2 = 3= 2 + 4
{0,487 + 0,604 ≈ 1,093 0,604 + 1,395 ≈ 2
По второму закону Кирхгофа
{ − 1 − 3 = 03 − 4 − 2 = 0
4 − 0,731 − 3,269 = 0 {3,269 − 4,175 − (−0,906) = 0
2) Определение токов цепи методом наложения
Для начала исключим ИТ и рассчитаем токи с XХ вместо него.
Рисунок 1- схема с исключением ИТ
Запишем значения токов
1 = 1,2142 = −0,4863 = 0,7294 = 0,486
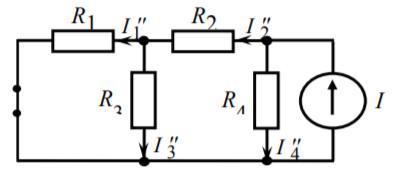
Затем проделаем тоже самое с ИН
Рисунок 2- схема с исключением ИН
Запишем значения токов
1 = −0,7262 = 1,0903 = 0,3644 = 0,910
Теперь заполним таблицу:
Источники |
|
1 |
2 |
3 |
4 |
U=4 В; I=0 |
I‘k |
1,214 |
-0,486 |
0,729 |
0,486 |
мА |
|
|
|
|
|
U=0 В; I=2 |
I‘’k |
-0,726 |
1,090 |
0,364 |
0,910 |
мА |
|
|
|
|
|
U=4 В; I=2 |
Ik |
1,214-0,726=0,488 |
0,604 |
1,093 |
1,396 |
мА |
|
|
|
|
|
3) Определение тока в ветви с сопротивлением R3 методом эквивалентного источника напряжения
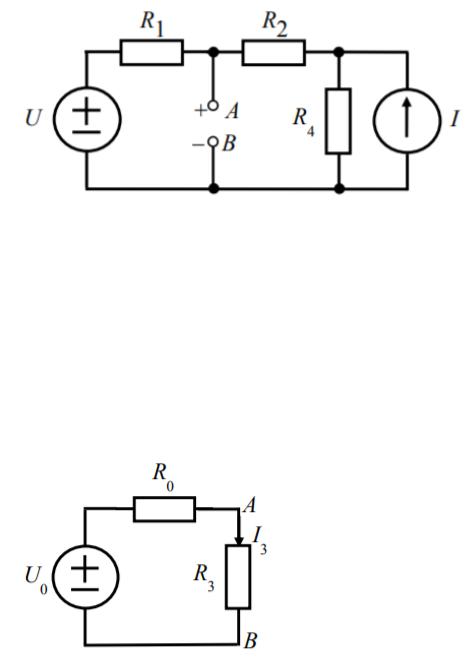
|
|
Рисунок 3- МЭИН |
Подключаем к цепи два источника U = 4 V и I = 2 mA |
||
Тогда 0 = 4,478 В |
3 = |
−1.091 |
Исключаем из схемы источники U и I и подключаем переключателем S3 потенциометр R5 |
||
и источник напряжения V2 |
к разомкнутым выводам А, В ветви 3. |
|
Измерим ток I 3 в ветви 3 |
|
|
3 = −1.091 .
Ток 3 равен по модулю равен ранее измеренному значение.
Проверим результаты измерений, решив схему методом эквивалентного источника напряжения.
Рисунок 4- цепь по отношению к ветви с сопротивлением R3
Найдем ток 3
3 |
= |
0 |
, 0 |
− напряжение ХХ |
||
3 |
+ 0 |
|||||
|
|
|
|
|||
0 − эквивалентное (выходное) сопротивление цепи.
Найдем 0:
Метод Контурных Токов
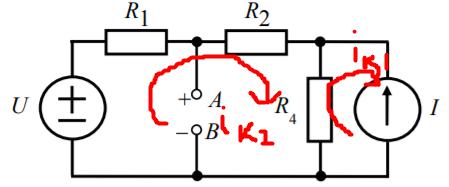
Рисунок 6- МКТ
|
|
|
|
|
|
|
= 2 10−3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
{ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
+ ( |
|
+ |
+ |
) = |
|
|
|
|
|
|
|
||||||||||||||||
|
4 |
1 |
|
1 |
|
|
|
|
2 |
4 |
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
= 2 10−3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
− 4 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
( 1 + 2 + 4) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
= 2 10−3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ |
|
|
|
|
|
4 − 3 103 2 10−3 |
|
|
|
|
|
|
|
||||||||||||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
(1.5 + 1.5 + 3) 103 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
= 2 10−3 А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ |
= − |
1 |
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
3000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
= − |
|
|
= − |
= − = 4 + |
1 |
|
1.5 103 |
= 4.5 |
||||||||||||||||||
|
|
||||||||||||||||||||||||||
0 |
|
|
|
|
1 |
|
|
|
|
|
1 |
1 |
2 |
1 |
|
3000 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем 0: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
= |
1 ( 2 |
+ 4) |
= |
1,5 (1,5 + 3) |
103 = 1.125 103 Ом |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
0 |
|
|
|
|
1 + 2 |
|
+ 4 |
1,5 + 1,5 + 3 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Найдем 3: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
= |
|
|
|
|
0 |
|
|
= |
|
|
|
|
4,5 |
|
|
= 1.09 10−3 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3 |
|
|
3 + 0 |
|
|
(3 + 1.125) 10^3 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Совпадает с результатом, данным в таблице 1.
4)Экспериментальная проверка принципа взаимности
Измерим ток 3 при отключенном ИТ
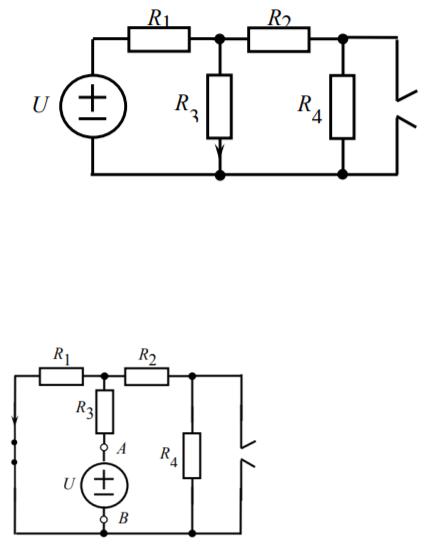
Рисунок 7- принцип взаимности
3 = 0,729 А
Перенесем ИТ во вторую ветвь
Рисунок 8- принцип взаимности с переносом ИН
При 2 = 4, 1 = 0,729 А
Ток резистора 3 равен току, рассчитанному в 3 пункте.

Ответы на вопросы
1. Каковы результаты контроля данных в п. 2.2.1?
Результаты контроля с помощью закона Кирхгофа показали верность измеренных данных.
2.Изменятся ли токи ветвей, если одновременно изменить полярность источника напряжения (ИН) и направление тока источника тока (ИТ) на противоположные?
Изменится лишь направление тока, величина силы тока не изменится.
3.Чему равно напряжение между узлами C и D цепи (рис. 2.1)?
= 1 + 2 = 0,731В -0.906 В = -0.175 В
4.Как изменить напряжение ИН, чтобы ток 1 в цепи рис. 2.1 стал равен нулю?
5.Почему цепь рис. 2.4, б при = реализует схему метода эквивалентного источника напряжения рис. 2.3, а?
Идея метода заключается в следующем: если в цепи любой сложности требуется найти единственную реакцию некоторой ветви, то схема относительно этой ветви может быть заменена эквивалентной схемой с единственным эквивалентным источником напряжения (или тока) с последовательно (или параллельно) включенным эквивалентным сопротивлением.
Так как в нашей работе сложности требуется найти единственную реакцию 3, то схема относительно этой ветви может быть заменена эквивалентной схемой с единственным эквивалентным источником напряжении с последовательно включенным эквивалентным сопротивлением.
Эквивалентные сопротивления равны, значит цепь рис. 2.4, б при = реализует схему метода эквивалентного источника напряжения рис. 2.3, а.
6.Чему будет равен ток 1 если ИН U поместить в ветвь 4, а ИТ отключить?
По методу эквивалентного ИН:
4 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4 + 123 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= |
|
3 1 |
|
+ = ( |
3 1,5 |
+ 1,5) 103 |
||||||||
|
|
|
|
|
|
|
|
|
||||||||
123 |
|
|
1 + 3 |
|
|
2 |
1,5 + 3 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
4 |
= |
|
|
|
= |
|
|
|
|
|
4 |
= 0,72 мА |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
+ |
|
|
|
|
|
3 |
|
||||||||
|
|
|
|
(3+2,5) 10 |
|
|
|
|
||||||||
|
|
4 |
123 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
3 |
|
= 0,72 10−3 |
3 103 |
||||
|
|
|
|
|
|
|
|
|
3 |
|||||||
1 |
|
|
+ |
|
|
|
+ |
|
|
|
||||||
|
|
|
|
|
|
|
(1,5+3) 10 |
|||||||||
|
|
1 |
123 |
|
1 |
|
3 |
|
|
|
|
|
||||
= 2500 Ом
=0,48 мА
7.Как проконтролировать результаты экспериментов в пп. 2.2.2, 2.2.3 и 2.2.4? Сравнением теоретических и практических значений.
Заключение
Таким образом, мы рассчитали одну схему тремя способами: методами наложения, эквивалентного источника и принципа взаимности. Для расчетов была использована программа Multisim, но и в ней были. Результаты расчетов схемы всеми тремя способами совпали с учетом погрешности.
