МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра «Теоретические основы электротехники»
Курсовая РАБОТА
по дисциплине «Теоретические основы электротехники»
Тема: «Тема: «Анализ линейной динамической цепи»
Студент гр. 9391 |
|
Фазекаш В.В |
Преподаватель |
|
Константинова Е.В. |
Санкт-Петербург
2020
Задание на курсовую работу
Студент: Фазекаш В.В
Группа: 9391
Тема работы: Анализ линейной динамической цепи.
Исходные данные:
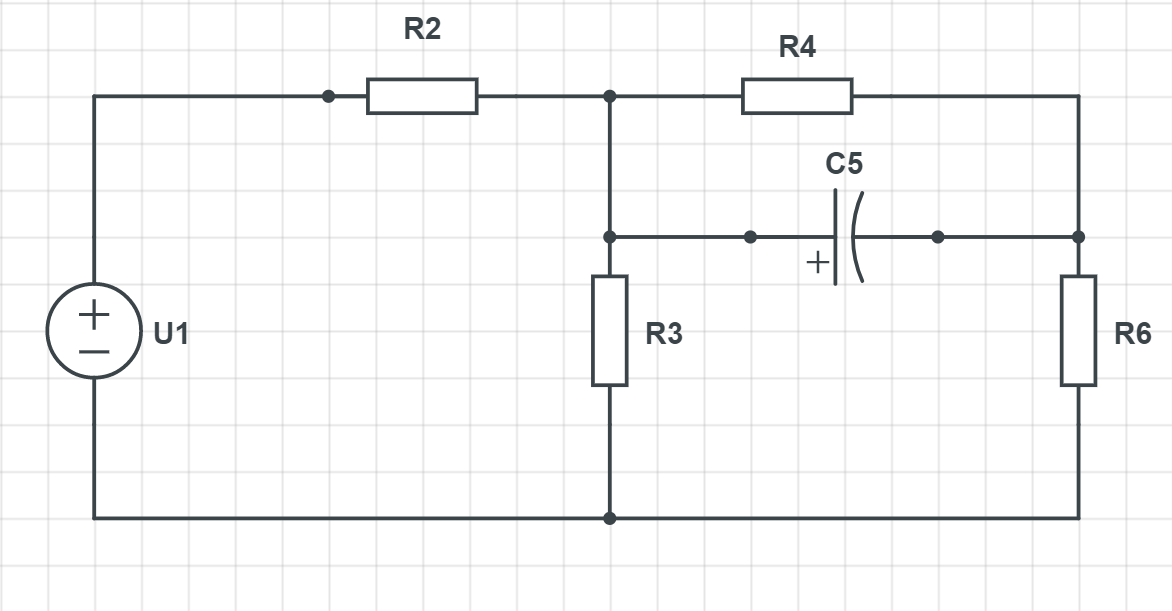
Рисунок 1 - Исследуемая схема
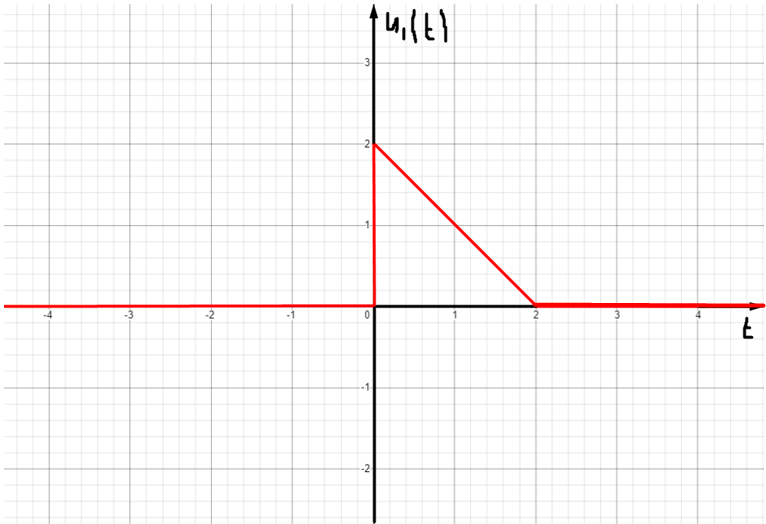
Рисунок 2 - Исследуемый сигнал
Параметры цепи:
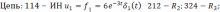
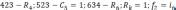
В курсовой работе необходимо выполнить:
1. Расчет переходного процесса во временной области при воздействиях произвольной формы
1.1. Найти переходную, импульсную, весовую характеристики цепи.
1. 2. Построить графики h1(t), h(t).
1.3. Получить выражение реакции цепи на аналитически заданное воздействие (с помощью интеграла свертки). Построить график полученной реакции.
1.4. Получить математическое описание графически заданного одиночного импульса.
1.5. Записать выражение реакции цепи на графически заданный одиночный импульс. Построить график полученной реакции.
2. Расчет переходного процесса с применением преобразования Лапласа.
2.1. Найти передаточную функцию цепи и проверить ее по схемам замещения.
2.2 Найти переходную и импульсную характеристики цепи.
2.3. Изобразить карту нулей и полюсов.
2.4. Найти изображение аналитически заданного воздействия.
2.5. Получить реакцию цепи на аналитически заданное воздействие.
2.6. Найти изображение графически заданного воздействия.
2.7. Получить реакцию цепи на графически заданное воздействие.
2.8. Записать формулы частотных характеристик цепи. Построить графики АЧХ и ФЧХ.
Дата выдачи задания: 6 октября
Дата сдачи КР на проверку
Дата защиты КР
Содержание
Введение……………………………………………………………….……..……...5 |
|
|
1.2Выражение реакции цепи на аналитически заданное воздействие (с помощью интеграла свертки). Построение графика полученной реакции..………………………………………………………..…………………….……..9 1.3 График h1(t), h(t)………………………………………………………...……..11 1.4 Математическое описание графически заданного одиночного импульса…..13 1.5 Реакция цепи на графически заданный одиночный импульс. Построение графика полученной реакции………………………………………...14 2.Расчет переходного процесса с применением преобразований Лапласа…16 2.1 Передаточная функция цепи и схема замещения……………………………..16 2.2 Карта нулей и полюсов…………………………………………………………19 2.3 Переходная и импульсная характеристики цепи……………………………..21 2.4 Изображение воздействия, заданного аналитически…………………...…….22 2.5 Реакция цепи на воздействие, заданное аналитически………………...……..22 2.6 Изображение воздействия, заданного графически……………………………22 2.7 Реакция цепи на воздействие, заданное графически ………………………...23 2.8 Формулы частотных характеристик цепи. Графики АЧХ и ФЧХ………..….24 |
Заключение…………………………………………………………………………26 |
Список использованных источников……………………...………………….…..27 |
|
введение
В курсовой работе представлен анализ динамических цепей первого порядка во временной области и с помощью операторного метода. В процессе работы следует определить характеристики динамической цепи, реакцию цепи на различные воздействия, частотные характеристики. Для выполнения поставленной задачи использовались: интеграл свёртки, ФДТ, ФДН, МКТ, таблица преобразований Лапласа.
Расчет переходных процессов во временной области при воздействиях произвольной формы
1.1 Переходная, импульсная, весовая характеристики цепи
1) t = 0–. По определению переходной характеристики в цепи, как бы
включается источник
напряжения единичного уровня в момент
t = 0, поэтому независимые начальные
условия равны нулю, т. е.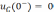 
.
2)
t>0.
Находим постоянную времени цепи, для
чего рассматриваем схему цепи в свободном
режиме, в которой по сравнению с исходной
схемой исключен источник напряжения
.
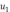Определяем эквивалентное сопротивление
относительно выводов С-элемента. Схема:
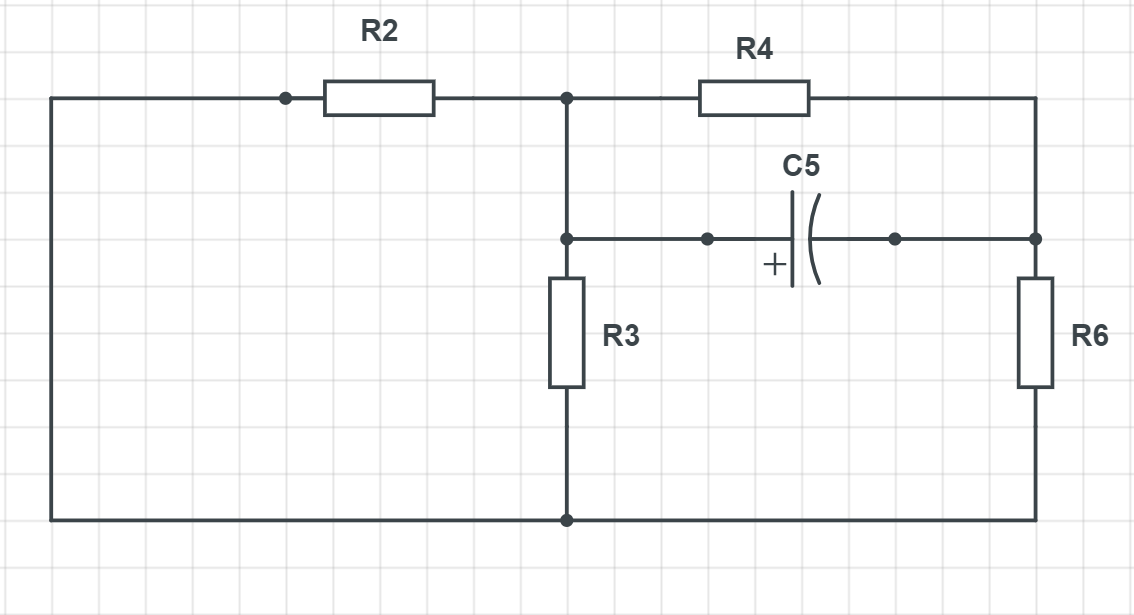
Рисунок 3 Исследуемая схема без u1
Рассмотрим получение
.
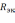Для этого заметим из исходной схемы,
что
Ом(так как
параллельны)
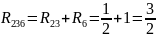Ом (так как
последовательны)
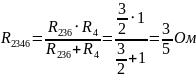(так
как параллельны)
Постоянная времени:
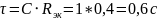
3)
.
Находим вынужденную составляющую
реакции
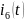по эквивалентной схеме замещения.
С-элемент заменяется на холостой ход.
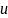= 1 В при t > 0,
считаем установившийся режим при
постоянном воздействии. Построим схему:
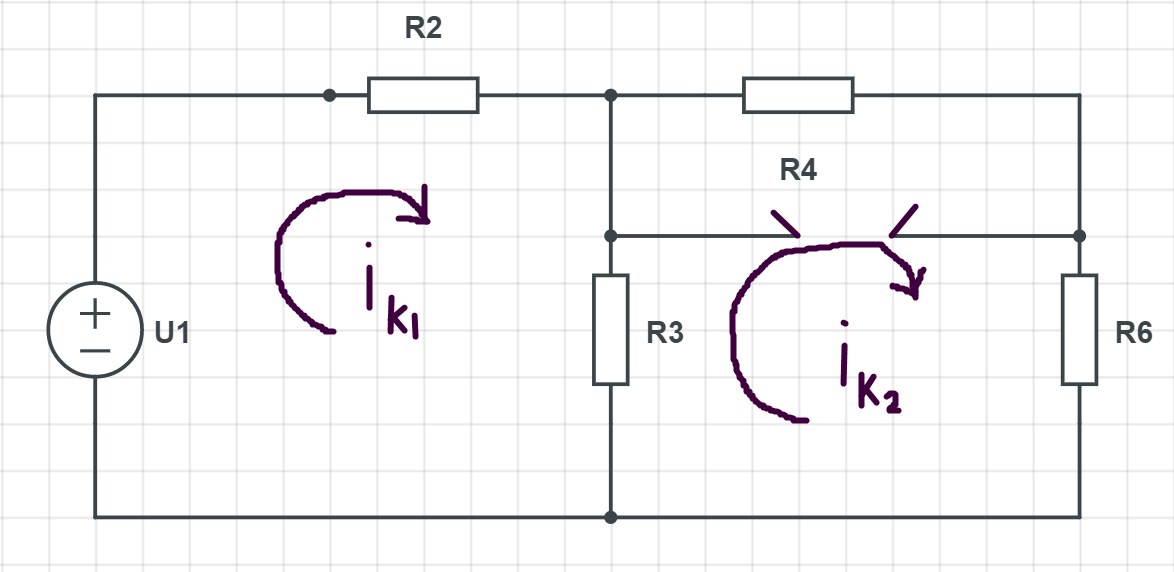
Рисунок 4 Схема с заменой С-элемента холостым ходом
Найдем i₆ метод Контурных токов:
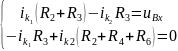
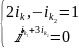
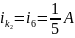(вынужденная
составляющая)
4) t
=
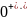Определяем зависимое начальное условие
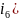по эквивалентной схеме замещения. Здесь
выводы индуктивного элемента разомкнуты,
так как
(
)
=
(
)=
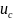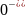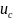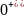0 (по теореме замещения C-элемент
при t = 0 заменяется на ИН с нулевым
напряжением, т. е. КЗ). При этом стоит
отметить, что
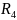располагается параллельно КЗ, следовательно
его исключаем их схемы.
Схема:
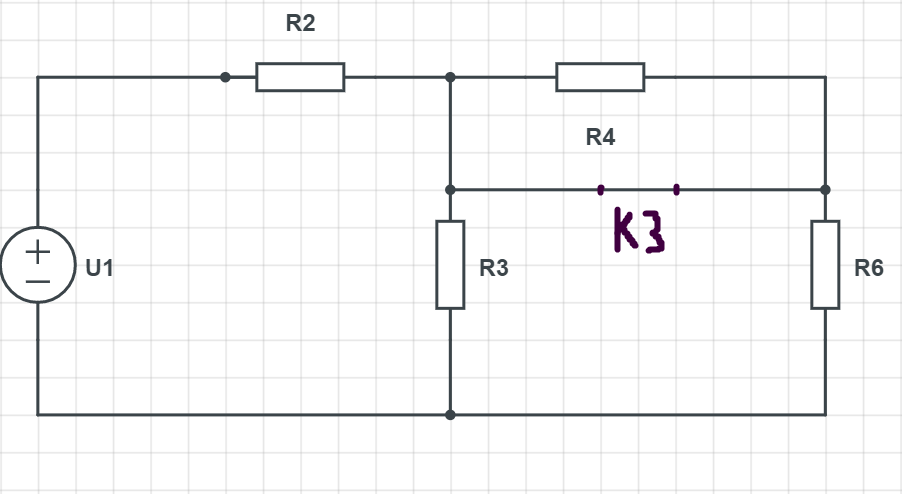
Рисунок 5 Схема в КЗ вместо С-элемента
В этой схеме
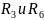соединены параллельно:
.
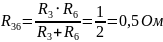Далее через ФДН
найдем
,
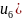при этом учтем, что
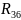и
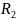соединены последовательно.
.
Дальше по з-ну Ома для участка цепи:
5) Найдем постоянную интегрирования А:
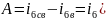
Запишем реакцию
:
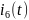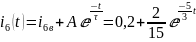
6) Найдем переходную характеристику
Переходная характеристика численно равна реакции цепи, следовательно, для любого момента времени можно записать:
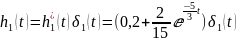
Импульсная
характеристика есть производная от
переходной характеристики:
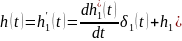
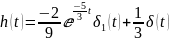
Весовая характеристика
равна интегралу от
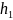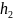(t)
:
(t)
=
*
=
(
)
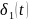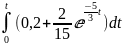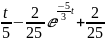(t)
=
1.2 Выражение реакции цепи на аналитически заданное воздействие (с помощью интеграла свертки). График полученной реакции
Определим при t >
0 реакцию
при воздействии
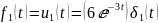с помощью интеграла свертки:
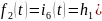
При чем:
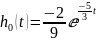(за
обозначим часть импульсной характеристики
без дельта функции)
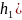
Следовательно,
=
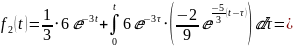
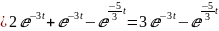
График
реакции
цепи
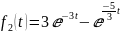на аналитически заданное воздействие:
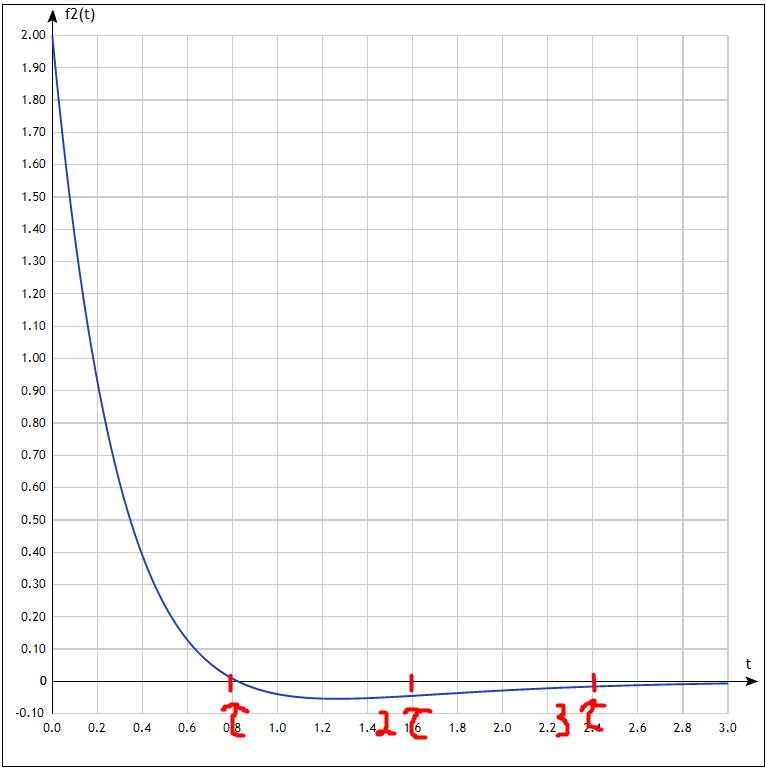
Рисунок 6 График реакции цепи
1.3 График h1(t), h(t)
Построим график переходной характеристики
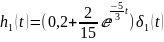
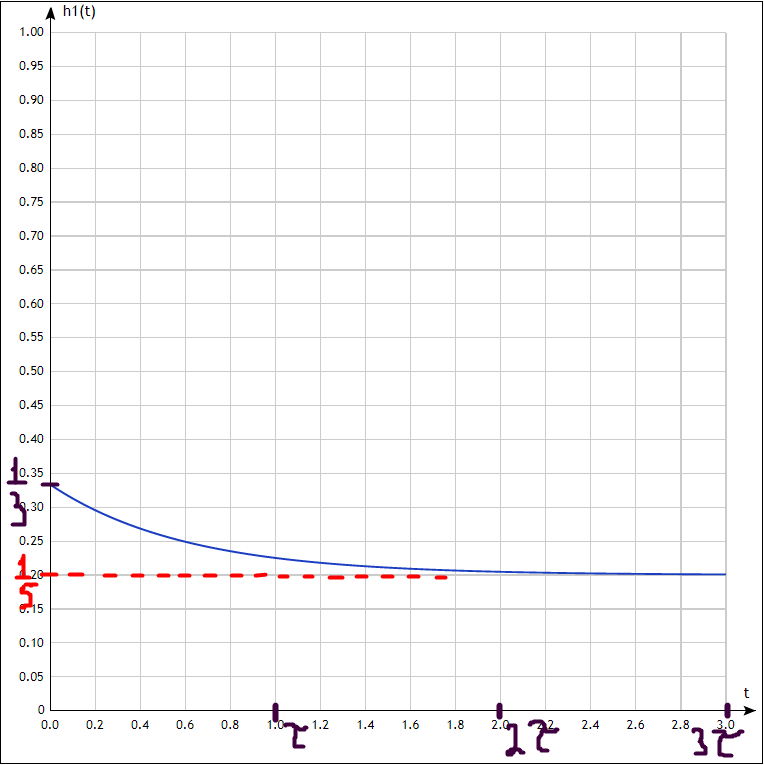
Рисунок 7 график переходной характеристики h1(t)
Построим график импульсной характеристики
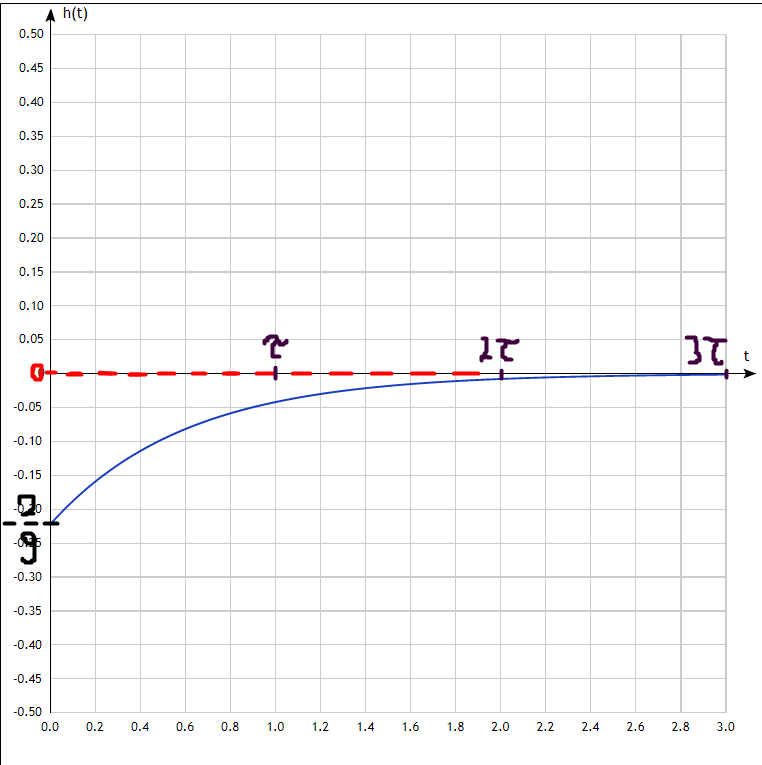
Рисунок 8 график импульсной характеристики
Математическое описание графически заданного одиночного импульса
Найдем реакцию
,
если воздействие
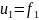имеет кусочно-линейную форму.
Затем запишем
функцию воздействия аналитически,
используя метод двойного дифференцирования.
Исходная кусочно-линейная функция
(0)=2,
(2)
= 0
Рисунок 9 Одиночный импульс
Построим график первой производной:
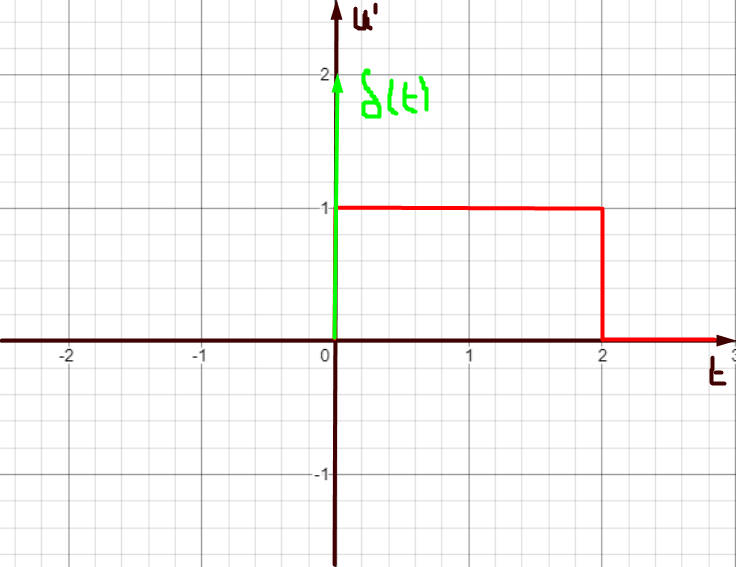
Рисунок 10 первая производная
Построим
график второй производной
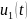
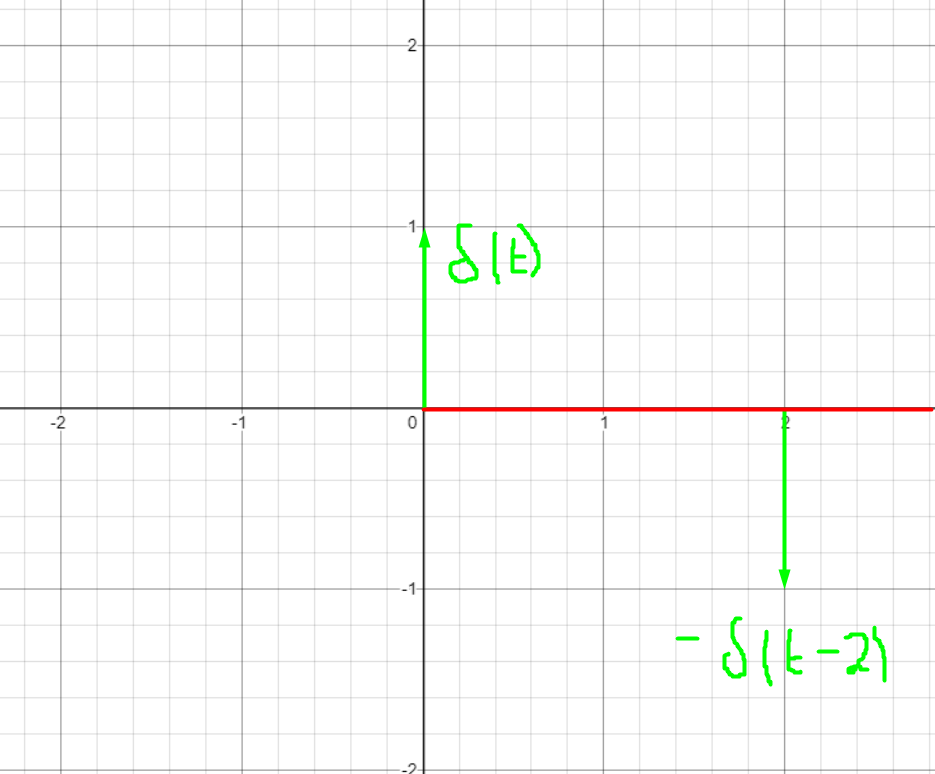
Рисунок 11 вторая производная
Из графиков получаем, что
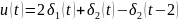
1.5 Реакция цепи на графически заданный одиночный импульс. График полученной реакции
Найдем реакцию цепи на графически заданный одиночный импульс
Из графиков мы знаем, что
Так же мы знаем, что
, и
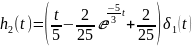
Тогда
=
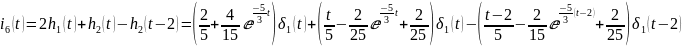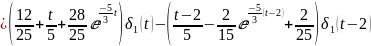
График реакция цепи на графически заданный одиночный импульс:
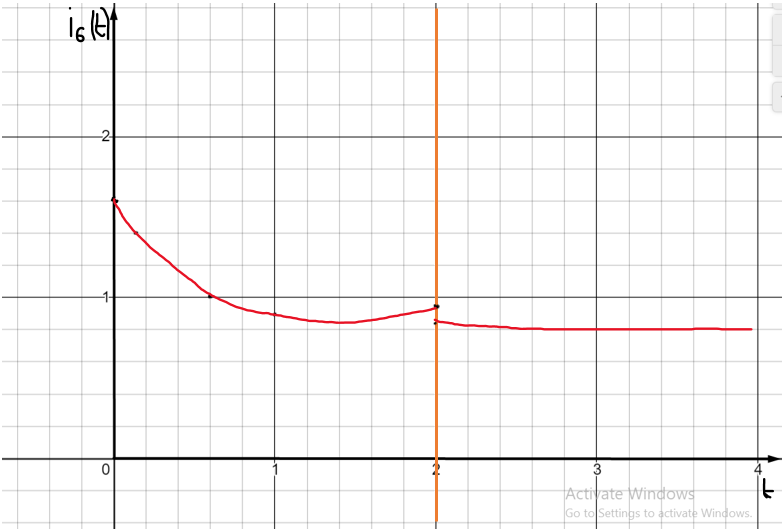
Рисунок 12 Реакция цепи на графически заданный одиночный импульс
Итак, мы рассчитали переходный процесс во временной области при воздействии произвольной формы